数理统计篇
概率论
条件概率
$x|\theta$ 和 $x,y|\theta$有什么关系
$x|\theta $表示在给定参数 $\theta$ 的情况下,随机变量 x 的概率分布。这意味着 x 的取值取决于参数 $\theta$。
$x,y|\theta$ 表示在给定参数 $\theta$ 的情况下,随机变量 x 和 y 的联合概率分布。这意味着 x 和 y 的取值都取决于参数 $\theta$。
因此,$x,y|\theta$ 中的信息比 $x|\theta$ 中的信息更丰富,因为前者提供了 x 和 y 的联合概率分布,而后者只提供了 x 的概率分布。
可以使用条件概率公式将 $x,y|\theta$ 转换为$ x|\theta $或者将$ x|\theta$ 转换为 $x,y|\theta$。
具体而言,根据条件概率公式,有:
$x,y|\theta = p(x,y|\theta) = p(x|\theta) * p(y|x,\theta)$
将上式中的 $p(y|x,\theta)$ 称为给定 x 和 $\theta$ 的条件下 y 的概率分布,它表示在已知 x 和 $\theta$ 的情况下,y 的可能取值的概率分布。如果已知这个条件下 y 的概率分布,就可以通过将它乘以$ x|\theta $来计算$ x,y|\theta$。
具体而言,有:
$p(x,y|\theta) = p(x|\theta) * p(y|x,\theta)$
$p(x|\theta) = p(x,y|\theta) / p(y|x,\theta)$
同样地,如果已知 $x,y|\theta$,可以通过条件概率公式将其转换为$ x|\theta$。具体而言,有:
$x|\theta = p(x|\theta) = ∫ p(x,y|\theta) dy$
其中,积分是在所有可能的 y 的取值上进行的,以保证 x 的概率分布的总和为1。
贝叶斯理论——Q&A
贝叶斯理论也是统计决策的思想吗
是的,贝叶斯理论是统计决策的一种思想。它是一种用于概率推断和统计推断的方法,可以通过先验概率和观察数据来推断出后验概率,从而帮助我们做出更好的决策。
在贝叶斯理论中,我们首先提出一个先验概率,这是我们对某个事件发生的预估概率,然后根据新的数据来更新这个概率,得到一个更准确的后验概率。在这个过程中,我们使用贝叶斯公式来计算后验概率。贝叶斯公式将先验概率和新的数据结合起来,计算出新的后验概率。
统计决策是一种通过概率和统计分析来做出决策的方法,其中贝叶斯理论是其中一种重要的思想。在统计决策中,我们使用统计方法来分析和评估不同的决策选项,以帮助我们做出最好的决策。贝叶斯理论提供了一种基于概率推断的方法来分析和评估不同的决策选项,因此它是统计决策中非常有用的一种思想。
统计决策思想是要最小化平均风险函数吗
是的,统计决策思想的目标通常是最小化平均风险函数。风险函数是一种用于度量决策结果的损失函数,而平均风险函数是指对所有可能的结果求出的期望风险。因此,最小化平均风险函数可以帮助我们找到最优的决策,以使期望的损失最小化。
在统计决策中,我们通常需要考虑多个决策选项和多个可能的结果。为了做出最优的决策,我们需要将不同决策选项和不同结果之间的风险进行比较。这需要使用一种统计方法来量化风险,并将其转化为数学模型。然后,我们可以通过最小化平均风险函数来找到最优的决策选项。
最小化平均风险函数的具体方法取决于具体问题的性质和条件。常用的方法包括贝叶斯决策理论、最小二乘法、最大似然估计等。无论使用哪种方法,最终目标都是找到一个最优的决策策略,使得期望风险最小化。
贝叶斯理论是怎么最小化风险决策的
贝叶斯理论可以用来最小化风险决策。它是一种基于概率推断的方法,通过先验概率和观察数据来计算后验概率,从而帮助我们做出最优的决策。
在贝叶斯理论中,我们首先提出一个先验概率,这是我们对某个事件发生的预估概率。然后,我们观察新的数据,并将其与先验概率相结合,得到一个更新后的后验概率。这个后验概率可以用来做出最优的决策,以最小化期望风险。
具体地说,假设我们面临一个决策问题,需要在多个决策选项中选择一个。我们可以使用贝叶斯理论来计算每个决策选项的期望风险,并选择期望风险最小的决策。
我们可以通过以下步骤来使用贝叶斯理论进行决策:
- 确定每个决策选项的潜在结果,并将每个结果与相应的风险关联起来。
- 对每个决策选项提出一个先验概率,这是在考虑任何观测数据之前我们对该选项的概率估计。
- 观察新的数据,并将其与先验概率相结合,得到一个更新的后验概率。
- 使用更新后的后验概率和与每个结果相关联的风险来计算每个决策选项的期望风险。
- 选择期望风险最小的决策选项作为最优的决策。
通过这种方式,我们可以使用贝叶斯理论来最小化期望风险,并做出最优的决策。
对于上面的回答,能给出一个离散问题的例子吗
当我们面对一个离散问题时,贝叶斯决策理论可以用来最小化期望损失函数,从而做出最优决策。
下面是一个离散问题的例子,假设我们需要决定在某一个天气条件下是否需要带伞:
- 我们将伞的状态分为两种情况:带伞和不带伞。
- 天气情况分为三种可能性:晴天、多云、雨天。
- 我们需要考虑两种类型的损失:如果我们带伞了,但是实际上不需要带伞,我们会浪费时间和精力;如果我们没有带伞,但实际上需要带伞,我们会被淋雨。
- 在这个例子中,我们可以使用贝叶斯决策理论来最小化期望损失函数。我们可以先提出先验概率,即在没有任何天气信息的情况下,我们决定带伞的概率。假设我们的先验概率是50%。
- 当我们得到新的天气信息时,我们可以计算每种天气条件下需要带伞的后验概率。例如,如果我们得到的天气是多云,我们可以使用贝叶斯定理来计算在多云天气下需要带伞的后验概率。
- 对于每种天气情况,我们可以计算出需要带伞和不需要带伞的期望损失。然后,我们选择期望损失最小的决策作为最优决策。
通过这个例子,我们可以看到贝叶斯决策理论如何在离散问题中被应用来最小化期望损失函数,从而帮助我们做出最优的决策。
上面回答中,期望损失怎么算
期望损失是指在给定先验概率和决策的情况下,所期望的损失大小。在离散问题中,期望损失可以通过以下方式计算:
假设我们有n个决策选项,每个选项的损失分别为L1, L2, …, Ln。对于第i个决策选项,假设先验概率为pi,后验概率为qi,则期望损失为:
E(Li) = L1 * q1 + L2 * q2 + … + Li * qi + … + Ln * qn
其中,qi为第i个决策选项的后验概率。通过计算每个决策选项的期望损失,我们可以确定最优的决策选项,即具有最小期望损失的选项。
在上面的带伞问题中,如果我们假设带伞的损失为1,不带伞的损失为2,则对于每种天气情况,我们可以计算需要带伞和不需要带伞的期望损失。例如,对于晴天,我们可以计算出在晴天下需要带伞和不需要带伞的期望损失分别为:
E(L1) = 1 * q1 + 2 * (1 - q1) E(L2) = 1 * q2 + 2 * (1 - q2)
其中,q1和q2分别为在晴天下需要带伞和不需要带伞的后验概率。然后,我们可以选择期望损失最小的决策作为最优决策。
上面回答中后验概率是怎么算的
在贝叶斯决策理论中,后验概率是指在给定观测数据和先验概率的情况下,对未知量的概率分布进行更新所得到的概率分布。在离散问题中,后验概率可以通过以下方式计算:
假设我们有k个假设,分别为H1, H2, …, Hk。对于第i个假设Hi,假设其先验概率为pi,似然函数为f(xi|Hi),其中xi为观测数据。则根据贝叶斯定理,第i个假设的后验概率为:
P(Hi|xi) = f(xi|Hi) * pi / sum(f(x|Hj) * pj), j=1,2,…,k
其中,sum(f(x|Hj) * pj)是对所有k个假设的似然函数和先验概率的乘积求和。
在上面的带伞问题中,假设先验概率为50%,即p(需要带伞) = 0.5,p(不需要带伞) = 0.5。如果我们得到了一条新的天气观测数据,例如观测到了多云天气,则需要计算在多云天气下需要带伞和不需要带伞的后验概率。假设在多云天气下需要带伞的似然函数为0.4,不需要带伞的似然函数为0.6,则根据贝叶斯定理,我们可以计算在多云天气下需要带伞和不需要带伞的后验概率为:
p(需要带伞|多云) = 0.4 * 0.5 / (0.4 * 0.5 + 0.6 * 0.5) = 0.4 / 1 = 0.4 p(不需要带伞|多云) = 0.6 * 0.5 / (0.4 * 0.5 + 0.6 * 0.5) = 0.6 / 1 = 0.6
因此,在多云天气下,需要带伞和不需要带伞的后验概率分别为0.4和0.6。通过计算每种天气情况下需要带伞和不需要带伞的后验概率,我们可以计算每种决策选项的期望损失,并选择期望损失最小的决策作为最优决策。
为什么求期望损失的时候,要用后验概率呢
在贝叶斯决策理论中,期望损失是在不同决策下,对损失函数的期望值进行比较来选择最优决策。而不同决策所对应的损失值是由不同假设成立的概率和对应的损失函数值共同决定的。
假设我们有k个假设,分别为H1, H2, …, Hk,每个假设Hi下有m个可能的决策,分别为d1, d2, …, dm。假设Li(dj)表示在假设Hi成立、选择决策dj时的损失值,则对于决策dj,它所对应的期望损失为:
E(Li(dj)) = sum(Li(dj) * P(Hi|X)), i=1,2,…,k
其中,P(Hi|X)表示在观测数据X给定的条件下,假设Hi成立的后验概率。这是因为在贝叶斯决策理论中,我们要考虑每个假设成立的可能性以及给定观测数据的信息,计算出每个决策的期望损失。由于观测数据已经给定,我们可以通过计算后验概率来考虑不同假设成立的可能性,并将其纳入期望损失的计算中。
因此,求期望损失时需要使用后验概率,以考虑不同假设成立的可能性对期望损失的影响。通过比较每种决策的期望损失,我们可以选择期望损失最小的决策作为最优决策。
x服从伽马分布,1/x服从什么分布,并分别说出他们的期望
如果 $X$ 服从参数为 $\alpha$ 和 $\beta$ 的伽马分布,即 $X \sim \operatorname{Gamma}(\alpha, \beta)$,其中 $\alpha, \beta > 0$,则 $Y=1/X$ 的分布是反演伽马分布,也称作反伽马分布。反演伽马分布的概率密度函数为:
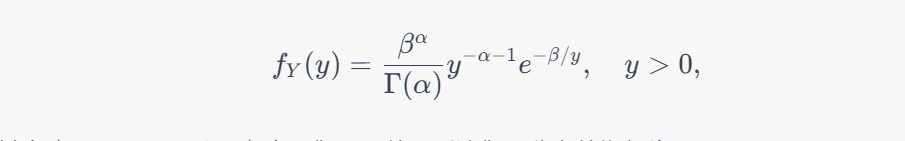
其中 $\Gamma(\cdot)$ 表示伽马函数。因此,我们可以写出 $Y$ 的分布符号为 $Y \sim \operatorname{InvGamma}(\alpha, \beta)$,其中 $\operatorname{InvGamma}$ 表示反演伽马分布。反演伽马分布的期望为:

反演伽马分布在很多贝叶斯统计推断中都有广泛应用,比如共轭先验等。
假设检验
在假设检验理论中,拒绝域是怎么推导出来的
在假设检验中,拒绝域是指当观察到的数据落在某个特定区域时,我们拒绝原假设的区域。拒绝域的推导涉及到以下几个步骤:
- 确定原假设和备择假设:首先需要确定要检验的原假设和备择假设。原假设通常表示我们要检验的“默认情况”,而备择假设则是我们想要检验的“替代情况”。
- 选择显著性水平:选择一个显著性水平,通常用α表示。显著性水平是指我们允许的假阳性错误的概率,通常选择0.05或0.01。
- 确定检验统计量:选择一个检验统计量,该统计量应该能够提供关于原假设的信息,以便我们可以对其进行检验。
- 建立拒绝域:基于显著性水平和检验统计量,建立拒绝域。拒绝域是一组观测值,如果我们观察到的数据落在这个区域内,我们将拒绝原假设。
- 计算检验统计量的值:根据收集到的数据计算检验统计量的值。
- 判断是否拒绝原假设:将计算出的检验统计量的值与拒绝域进行比较。如果检验统计量的值落在拒绝域内,则拒绝原假设;否则,接受原假设。
总的来说,拒绝域的推导是通过基于显著性水平和检验统计量来确定的。在选择拒绝域时,需要权衡拒绝原假设和接受原假设的概率以及检验统计量的准确性。
中心极限定理
n个两个分布的和相加可以近似于二项分布吗?
如果 $X_1, X_2, \ldots, X_n$ 是 $n$ 个独立同分布的随机变量,且每个随机变量只能取 $0$ 或 $1$ 两个值,即 $X_i$ 只能取 $0$ 或 $1$,且其期望和方差分别为 $E(X_i) = p$ 和 $\text{Var}(X_i) = p(1-p)$,其中 $0<p<1$,那么将这 $n$ 个随机变量相加的和 $S_n = \sum_{i=1}^{n}X_i$ 近似服从二项分布 $\text{Bin}(n, p)$。
这是由于根据中心极限定理,当 $n$ 足够大时,$S_n$ 的分布会趋近于正态分布。具体来说,当 $n$ 足够大时,有:
$$S_n \approx N(np, np(1-p))$$
这意味着可以用正态分布来近似描述 $S_n$ 的分布。而二项分布 $\text{Bin}(n, p)$ 也可以近似用正态分布来描述,即:
$$\text{Bin}(n, p) \approx N(np, np(1-p))$$
因此,将 $n$ 个独立同分布的随机变量相加的和近似为二项分布 $\text{Bin}(n, p)$ 是合理的。
机器学习篇
损失
为什么要计算log 概率密度函数?
在机器学习和统计建模中,通常需要计算概率密度函数或概率质量函数。概率密度函数或概率质量函数的值描述了观测到某个事件或数据点的概率。
然而,在实际应用中,概率值通常非常小,可能会导致数值下溢或浮点数舍入误差。为了解决这个问题,我们可以使用对数变换来计算概率密度函数或概率质量函数的对数值,这个对数值通常被称为对数概率密度函数或对数概率质量函数。对数值的计算可以避免数值下溢和浮点数舍入误差,并提高计算的稳定性和精度。
在 PyTorch 中,
torch.distributions模块中的分布类通常提供两个方法来计算概率密度函数或概率质量函数的值:log_prob()和prob()。log_prob()方法计算对数概率密度函数或对数概率质量函数的值,而prob()方法计算概率密度函数或概率质量函数的值。由于log_prob()方法计算的是对数值,它通常比prob()方法更稳定和精确。因此,在 PyTorch 中,计算对数概率密度函数或对数概率质量函数的值通常更常见。当然,在一些特定情况下,比如需要计算分布的熵(entropy)时,我们可能会使用
prob()方法。
算法
SPSA (Simultaneous Perturbation Stochastic Approximation)和RM (Robbins Monro)区别和联系
SPSA (Simultaneous Perturbation Stochastic Approximation) 和 RM (Robbins Monro) 都是随机优化算法,用于寻找非线性、非光滑函数的全局最优解。它们之间的区别和联系如下:
区别:
- SPSA 是一种随机梯度下降算法,而 RM 是一种随机逼近算法;
- SPSA 使用随机扰动来估计梯度,而 RM 使用随机样本来估计梯度;
- SPSA 适用于高维优化问题,而 RM 适用于低维优化问题;
- SPSA 不需要对目标函数进行任何假设,而 RM 假设目标函数是凸函数;
- SPSA 可以使用一阶梯度信息,而 RM 可以使用一阶或二阶梯度信息。
联系:
- 两种算法都是全局优化算法,可以在非线性、非凸函数的搜索空间中寻找全局最优解;
- 都使用随机性来跳出局部最优解,以避免陷入局部最优解;
- 都需要调整算法的参数,以达到最优效果。
总之,SPSA 和 RM 是两种不同的优化算法,它们的主要区别在于梯度估计的方法和算法的适用范围。

