启发式算法

原文地址：范叶亮|莫烦|黄少兵

1 启发式算法

启发式算法（Heuristic Algorithm）是解优化问题的一种算法。它是借助于对问题的具体分析或计算经验等方面的启示，能够较快地给出问题满意解的算法。这里说的满意解，一般不是问题的最优解，而是较好的可行解。

数学辞海.第二卷[M].南京:东南大学出版社.2002.129-129

2 启发式算法分类

启发式算法可以分为传统启发式算法[1]、元启发式算法（Meta-heuristic algorithm）[1]、超启发式算法（Hyper-heuristic algorithm）[2]。

传统启发式算法包括构造型方法、局部搜索算法、松弛方法、解空间缩减算法等[1]。

元启发式算法包括禁忌搜索算法、模拟退火算法、遗传算法、蚁群优化算法、人工神经网络算法等[1]。

超启发式算法定义[2]：

超启发式算法提供了某种高层策略（high-level strategy, HLS），通过操纵或管理一组底层启发式算子（low-level heuristics, LLH），以获得新启发式算法。

现有超启发式算法可以大致分为4类：基于随机选择（random selection）、基于贪心（greedy）策略、基于元启发式算法和基于学习的超启发式算法。

启发式算法 (Heuristic Algorithms)

启发式算法 (Heuristic Algorithms) 是相对于最优算法提出的。一个问题的最优算法是指求得该问题每个实例的最优解. 启发式算法可以这样定义 1：一个基于直观或经验构造的算法，在可接受的花费 (指计算时间、占用空间等) 下给出待解决组合优化问题每一个实例的一个可行解，该可行解与最优解的偏离程度不一定事先可以预计。

在某些情况下，特别是实际问题中，最优算法的计算时间使人无法忍受或因问题的难度使其计算时间随问题规模的增加以指数速度增加，此时只能通过启发式算法求得问题的一个可行解。

利用启发式算法进行目标优化的一些优缺点如下：

优点	缺点
1. 算法简单直观，易于修改 2. 算法能够在可接受的时间内给出一个较优解	1. 不能保证为全局最优解 2. 算法不稳定，性能取决于具体问题和设计者经验

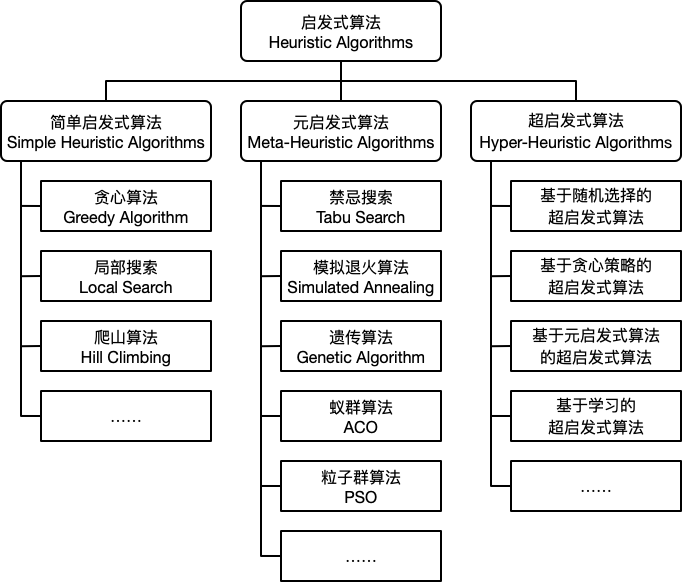
启发式算法简单的划分为如下三类：简单启发式算法 (Simple Heuristic Algorithms)，元启发式算法 (Meta-Heuristic Algorithms) 和 **超启发式算法 (Hyper-Heuristic Algorithms)**。

简单启发式算法 (Simple Heuristic Algorithms)

贪心算法 (Greedy Algorithm)

贪心算法是指一种在求解问题时总是采取当前状态下最优的选择从而得到最优解的算法。贪心算法的基本步骤定义如下：

1. 确定问题的最优子结构。
2. 设计递归解，并保证在任一阶段，最优选择之一总是贪心选择。
3. 实现基于贪心策略的递归算法，并转换成迭代算法。

对于利用贪心算法求解的问题需要包含如下两个重要的性质：

1. 最优子结构性质。当一个问题具有最优子结构性质时，可用 动态规划 法求解，但有时用贪心算法求解会更加的简单有效。同时并非所有具有最优子结构性质的问题都可以利用贪心算法求解。
2. 贪心选择性质。所求问题的整体最优解可以通过一系列局部最优的选择 (即贪心选择) 来达到。这是贪心算法可行的基本要素，也是贪心算法与动态规划算法的主要区别。

贪心算法和动态规划算法之间的差异如下表所示：

贪心算法	动态规划
每个阶段可以根据选择当前状态最优解快速的做出决策	每个阶段的选择建立在子问题的解之上
可以在子问题求解之前贪婪的做出选择	子问题需先进行求解
自顶向下的求解	自底向上的求解 (也可采用带备忘录的自顶向下方法)
通常情况下简单高效	效率可能比较低

局部搜索 (Local Search) 和爬山算法 (Hill Climbing)

局部搜索算法基于贪婪思想，从一个候选解开始，持续地在其邻域中搜索，直至邻域中没有更好的解。对于一个优化问题：

$$\min f(x),x\in\mathbb{R}^n\quad$$

其中，$f(x)$ 为目标函数。搜索可以理解为从一个解移动到另一个解的过程，令 $s(x)$表示通过移动得到的一个解，$S(x)$ 为从当前解出发所有可能的解的集合 (邻域)，则局部搜索算法的步骤描述如下：

1. 初始化一个可行解 $x$。
2. 在当前解的邻域内选择一个移动后的解$s(x)$，使得 $f(s(x))<f(x),s(x)\in S(x)$，如果不存在这样的解，则 $x$为最优解，算法停止。
3. 令 $x=s(x)$，重复步骤 2。

当我们的优化目标为最大化目标函数 $f(x)$时，这种局部搜索算法称之为爬山算法。

元启发式算法 (Meta-Heuristic Algorithms)

元启发式算法 (Meta-Heuristic Algorithms) 是启发式算法的改进，通常使用随机搜索技巧，可以应用在非常广泛的问题上，但不能保证效率。本节部分内容参考了《智能优化方法》 和《现代优化计算方法》。

禁忌搜索 (Tabu Search)

禁忌搜索 (Tabu Search) 是由 Glover 提出的一种优化方法。禁忌搜索通过在解邻域内搜索更优的解的方式寻找目标的最优解，在搜索的过程中将搜索历史放入禁忌表 (Tabu List) 中从而避免重复搜索。禁忌表通过模仿人类的记忆功能，禁忌搜索因此得名。

在禁忌搜索算法中，禁忌表用于防止搜索过程出现循环，避免陷入局部最优。对于一个给定长度的禁忌表，随着新的禁忌对象的不断进入，旧的禁忌对象会逐步退出，从而可以重新被访问。禁忌表是禁忌搜索算法的核心，其功能同人类的短时记忆功能相似，因此又称之为“短期表”。

在某些特定的条件下，无论某个选择是否包含在禁忌表中，我们都接受这个选择并更新当前解和历史最优解，这个选择所满足的特定条件称之为渴望水平。

一个基本的禁忌搜索算法的步骤描述如下：

1. 给定一个初始可行解，将禁忌表设置为空。
2. 选择候选集中的最优解，若其满足渴望水平，则更新渴望水平和当前解；否则选择未被禁忌的最优解。
3. 更新禁忌表。
4. 判断是否满足停止条件，如果满足，则停止算法；否则转至步骤 2。

模拟退火 (Simulated Annealing)

模拟退火 (Simulated Annealing) 是一种通过在邻域中寻找目标值相对小的状态从而求解全局最优的算法，现代的模拟退火是由 Kirkpatrick 等人于 1983 年提出 4。模拟退火算法源自于对热力学中退火过程的模拟，在给定一个初始温度下，通过不断降低温度，使得算法能够在多项式时间内得到一个近似最优解。

对于一个优化问题 $\min\ f(x)$，模拟退火算法的步骤描述如下：

1. 给定一个初始可行解 $x_0$，初始温度$T_0$和终止温度 $T_t$，令迭代计数为 $k$。
2. 随机选取一个邻域解 $x_k$，计算目标函数增量 $\Delta f=f\left(x_k\right)-f\left(x\right)$。若 $\Delta f<0$，则令 $x=x_k$；否则生成随机数 $\xi =U(0,1)$，若随机数小于转移概率 $P(\Delta f,T)$，则令 $x=x_k$。
3. 降低温度 $T$。
4. 若达到最大迭代次数 $k_{max}$ 或最低温度 $T_f$，则停止算法；否则转至步骤 2。

整个算法的伪代码如下：

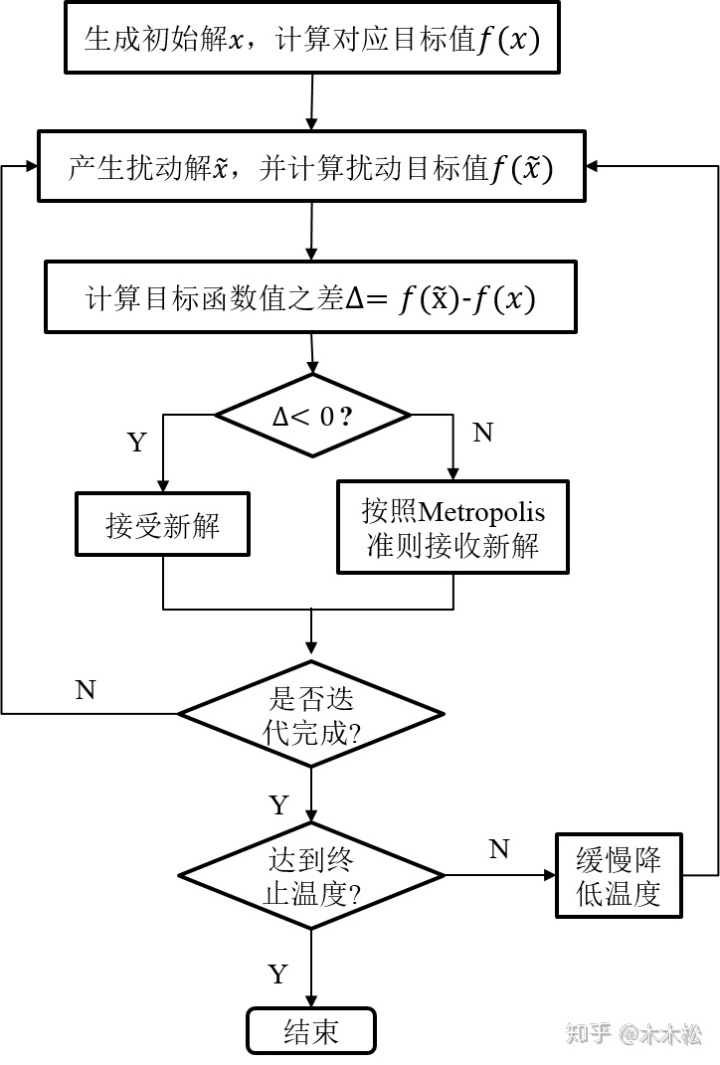
在进行邻域搜索的过程中，当温度较高时，搜索的空间较大，反之搜索的空间较小。类似的，当 $\Delta f>0$ 时，转移概率的设置也同当前温度的大小成正比。常用的降温函数有两种：

1. $T_{k+1}=T_k*r$,其中$r\in (0.95,0.99)$，$r$的设置越大，温度下降的越快
2. $T_{k+1}=T_k-\Delta T$，其中$\Delta T$为每一步温度的减少量

初始温度和终止温度对算法的影响较大，相关参数设置的细节请参见参考文献。

模拟退火算法是对局部搜索和爬山算法的改进，我们通过如下示例对比两者之间的差异。假设目标函数如下：

$$f\left(x,y\right)=e^{-\left(x^{2}+y^{2}\right)}+2e^{-\left(\left(x-1.7\right)^{2}+\left(y-1.7\right)^2\right)}$$

优化问题定义为：

$$\max f(x,y),x\in[-2,4],y\in[-2,4]$$

我们分别令初始解为 $(1.5,−1.5)$ 和 $(3.5,0.5)$，下图 (上) 为爬山算法的结果，下图 (下) 为模拟退火算法的结果。

其中，白色 的大点为初始解位置，粉色 的大点为求解的最优解位置，颜色从白到粉描述了迭代次数。从图中不难看出，由于局部最大值的存在，从不同的初始解出发，爬山算法容易陷入局部最大值，而模拟退火算法则相对稳定。

再看下面这个图：

import numpy as np
import matplotlib.pyplot as plt
import random


class SA(object):
    def __init__(self, interval, tab='min', T_max=10000, T_min=1, iterMax=1000, rate=0.95):
        self.interval = interval  # 给定状态空间 - 即待求解空间
        self.T_max = T_max  # 初始退火温度 - 温度上限
        self.T_min = T_min  # 截止退火温度 - 温度下限
        self.iterMax = iterMax  # 定温内部迭代次数
        self.rate = rate  # 退火降温速度
        #############################################################
        self.x_seed = random.uniform(interval[0], interval[1])  # 解空间内的种子
        self.tab = tab.strip()  # 求解最大值还是最小值的标签: 'min' - 最小值；'max' - 最大值
        #############################################################
        self.solve()  # 完成主体的求解过程
        self.display()  # 数据可视化展示

    def solve(self):
        temp = 'deal_' + self.tab  # 采用反射方法提取对应的函数

        if hasattr(self, temp):
            deal = getattr(self, temp)
        else:
            exit('>>>tab标签传参有误："min"|"max"<<<')
        x1 = self.x_seed
        T = self.T_max
        while T >= self.T_min:
            for i in range(self.iterMax):
                f1 = self.func(x1)
                delta_x = random.random() * 2 - 1
                if x1 + delta_x >= self.interval[0] and x1 + delta_x <= self.interval[1]:  # 将随机解束缚在给定状态空间内
                    x2 = x1 + delta_x
                else:
                    x2 = x1 - delta_x
                f2 = self.func(x2)
                delta_f = f2 - f1
                x1 = deal(x1, x2, delta_f, T)
            T *= self.rate
        self.x_solu = x1  # 提取最终退火解


    def func(self, x):  # 状态产生函数 - 即待求解函数
        value = np.sin(x ** 2) * (x ** 2 - 5 * x)
        return value


    def p_min(self, delta, T):  # 计算最小值时，容忍解的状态迁移概率
        probability = np.exp(-delta / T)
        return probability


    def p_max(self, delta, T):
        probability = np.exp(delta / T)  # 计算最大值时，容忍解的状态迁移概率
        return probability


    def deal_min(self, x1, x2, delta, T):
        if delta < 0:  # 更优解
            return x2
        else:  # 容忍解
            P = self.p_min(delta, T)
        if P > random.random():
            return x2
        else:
            return x1


    def deal_max(self, x1, x2, delta, T):
        if delta > 0:  # 更优解
            return x2
        else:  # 容忍解
            P = self.p_max(delta, T)
        if P > random.random():
            return x2
        else:
            return x1


    def display(self):
        print('seed: {}\nsolution: {}'.format(self.x_seed, self.x_solu))
        plt.figure(figsize=(6, 4))
        x = np.linspace(self.interval[0], self.interval[1], 300)
        y = self.func(x)
        plt.plot(x, y, 'g-', label='function')
        plt.plot(self.x_seed, self.func(self.x_seed), 'bo', label='seed')
        plt.plot(self.x_solu, self.func(self.x_solu), 'r*', label='solution')
        plt.title('solution = {}'.format(self.x_solu))
        plt.xlabel('x')
        plt.ylabel('y')
        plt.legend()
        plt.savefig('SA.png', dpi=500)
        plt.show()
        plt.close()


if __name__ == '__main__':
    SA([-5, 5], 'max')

遗传算法 (Genetic Algorithm)

遗传算法 (Genetic Algorithm, GA) 是由 John Holland 提出，其学生 Goldberg 对整个算法进行了进一步完善 5。算法的整个思想来源于达尔文的进化论，其基本思想是根据问题的目标函数构造一个适应度函数 (Fitness Function)，对于种群中的每个个体 (即问题的一个解) 进行评估 (计算适应度)，选择，交叉和变异，通过多轮的繁殖选择适应度最好的个体作为问题的最优解。算法的整个流程如下所示：

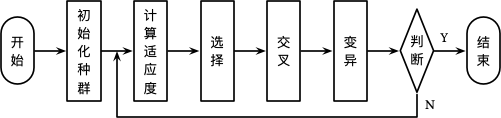
初始化种群

在初始化种群时，我们首先需要对每一个个体进行编码，常用的编码方式有二进制编码，实值编码 6，矩阵编码 7，树形编码等。以二进制为例 (如下不做特殊说明时均以二进制编码为例)，对于 $p∈{0,1,…,100} $中 $p_i=50$ 可以表示为：
$$x_i=50_{10}=0110010_2$$

对于一个具体的问题，我们需要选择合适的编码方式对问题的解进行编码，编码后的个体可以称之为一个染色体。则一个染色体可以表示为：

$$x={p_1,p_2,…,p_m}$$

其中，$m$为染色体的长度或编码的位数。初始化种群个体共 $n$个，对于任意一个个体染色体的任意一位 $i$，随机生成一个随机数 $rand\in (0,1)$，若 $rand>0.5$，则 $p_i=1$，否则$p_i=0$。

计算适应度

适应度为评价个体优劣程度的函数 $f(x)$，通常为问题的目标函数，对最小化优化问题$f\left(x\right)=-\min\sum\mathcal{L}\left(\hat{y},y\right)$,中 $\mathcal{L}$为损失函数。

选择

对于种群中的每个个体，计算其适应度，记第 $i$个个体的适应度为 $F_i=f(x_i)$。则个体在一次选择中被选中的概率为：

$$P_i=\dfrac{F_i}{\sum_{i=1}^n F_i}$$

为了保证种群的数量不变，我们需要重复 $n$次选择过程，单次选择采用轮盘赌的方法。利用计算得到的被选中的概率计算每个个体的累积概率：

$$CP_0=0\ CP_i=\sum_{j=1}^i P_i$$

对于如下一个示例：

对于如下一个示例：

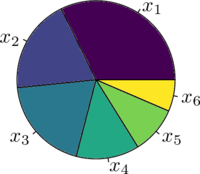
指标 \ 个体	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$
适应度 (F)	100	60	60	40	30	20
概率 (P)	0.322	0.194	0.194	0.129	0.097	0.064
累积概率 (CP)	0.322	0.516	0.71	0.839	0.936	1

每次选择时，随机生成 $rand\in U(0,1)$，当 $CP_{i-1}≤rand≤CP_i $时，选择个体 $x_i$。选择的过程如同在下图的轮盘上安装一个指针并随机旋转，每次指针停止的位置的即为选择的个体。

交叉

交叉运算类似于染色体之间的交叉，常用的方法有单点交叉，多点交叉和均匀交叉等。

• 单点交叉：在染色体中选择一个切点，然后将其中一部分同另一个染色体的对应部分进行交换得到两个新的个体。交叉过程如下图所示：

• 多点交叉：在染色体中选择多个切点，对其任意两个切点之间部分以概率 $P_c$ 进行交换，其中$P_c$为一个较大的值，例如 $P_m=0.9$。两点交叉过程如下图所示：

• 均匀交叉：染色体任意对应的位置以一定的概率进行交换得到新的个体。交叉过程如下图所示：

变异

变异即对于一个染色体的任意位置的值以一定的概率 $P_m$ 发生变化，对于二进制编码来说即反转该位置的值。其中 $P_m$为一个较小的值，例如 $P_m=0.05$。

小结

在整个遗传运算的过程中，不同的操作发挥着不同的作用：

1. 选择：优胜劣汰，适者生存。
2. 交叉：丰富种群，持续优化。
3. 变异：随机扰动，避免局部最优。

除此之外，对于基本的遗传算法还有多种优化方法，例如：精英主义，即将每一代中的最优解原封不动的复制到下一代中，这保证了最优解可以存活到整个算法结束。

示例 - 商旅问题

以 商旅问题 为例，利用 GA 算法求解中国 34 个省会城市的商旅问题。求解代码利用了 Deap 库，结果可视化如下图所示：

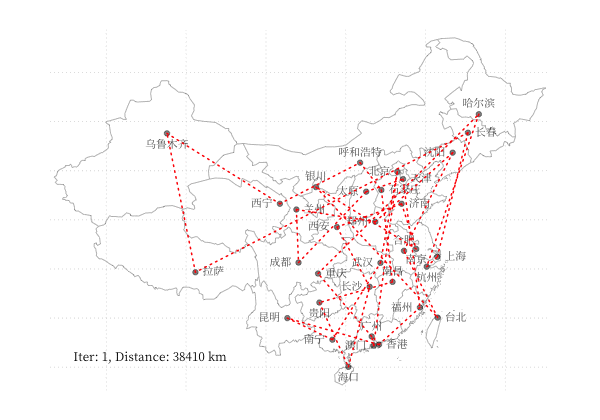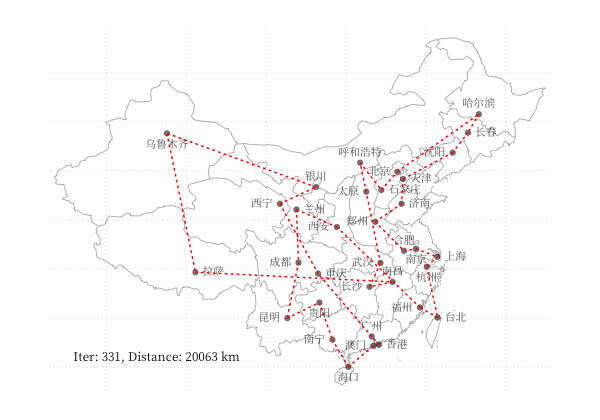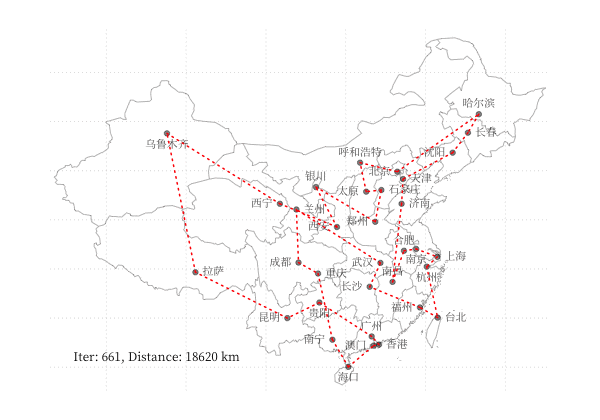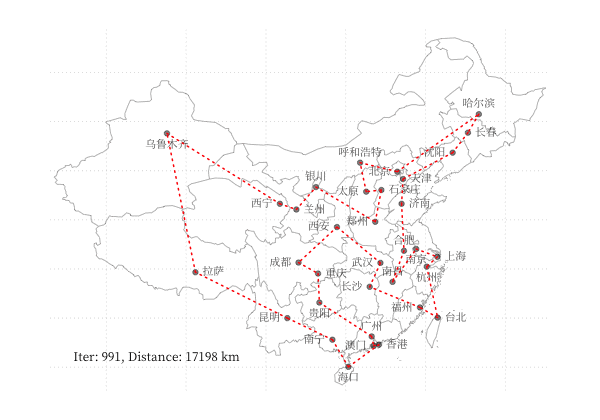
一个更有趣的例子是利用 GA 算法，使用不同颜色和透明度的多边形的叠加表示一张图片，在线体验详见 这里，下图为不同参数下的蒙娜丽莎图片的表示情况：

实践

原文地址

上面提到遗传算法是用来解决最优化问题的，下面我将以求二元函数：

def F(x, y):
	return 3*(1-x)**2*np.exp(-(x**2)-(y+1)**2)- 10*(x/5 - x**3 - y**5)*np.exp(-x**2-y**2)- 1/3**np.exp(-(x+1)**2 - y**2)

在 $x\in[-3, 3], y\in[-3, 3]$范围里的最大值为例子来详细讲解遗传算法的每一步。该函数的图像如下图：

通过旋转视角可以发现，函数在这个局部的最大值大概在当 $x \approx 0,y\approx1.5$时，函数值取得最大值，这里的$x,y$的取值就是我们最后要得到的结果。

先直观看一下算法过程：

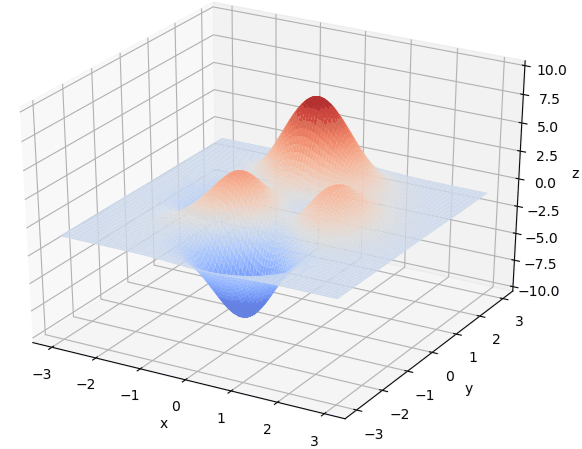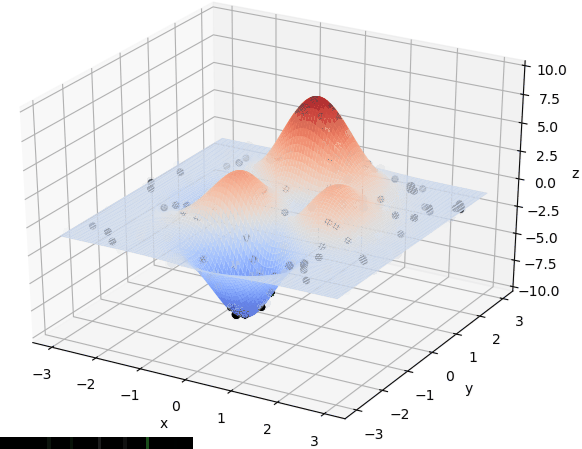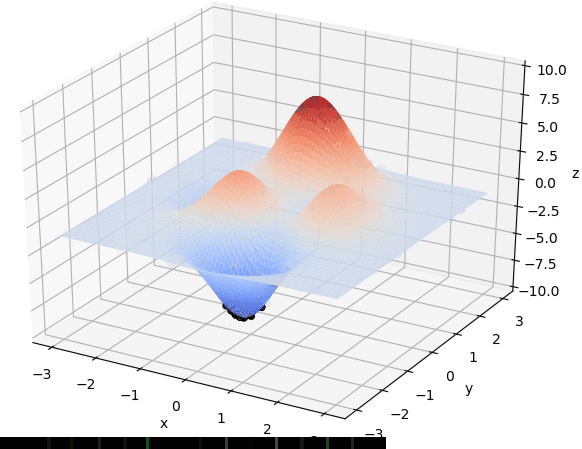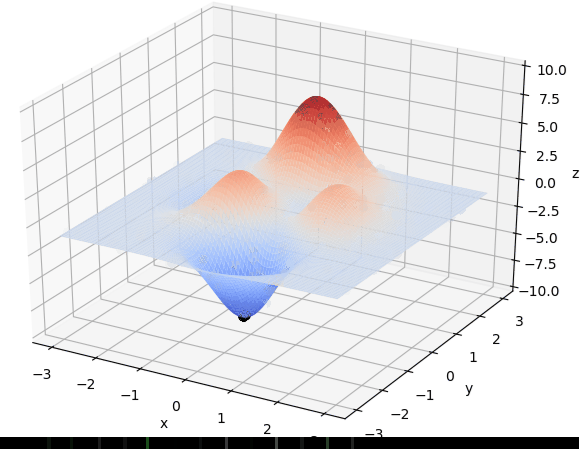
首先我们生成了200个随机的（x,y）对，将(x, y)坐标对带入要求解的函数F(x,y)中，根据适者生存，我们定义使得函数值F(x,y)越大的(x,y)对越适合环境，从而这些适应环境的(x,y)对更有可能被保留下来，而那些不适应该环境的(x,y)则有很大几率被淘汰，保留下来的点经过繁殖产生新的点，如此进化下去最后留下的大部分点都是试应环境的点，即在最高点附近。下图为算法执行结果，和上面的分析$x \approx 0,y\approx1.5$相近。

种群和个体的概念

遗传算法启发自进化理论，而我们知道进化是由种群为单位的，种群是什么呢？维基百科上解释为：在生物学上，是在一定空间范围内同时生活着的同种生物的全部个体。显然要想理解种群的概念，又先得理解个体的概念，在遗传算法里，个体通常为某个问题的一个解，并且该解在计算机中被编码为一个向量表示！ 我们的例子中要求最大值，所以该问题的解为一组可能的( x , y ) 的取值。比如( x = 2.1 , y = 0.8 ) , ( x = − 1.5 , y = 2.3 )…就是求最大值问题的一个可能解，也就是遗传算法里的个体，把这样的一组一组的可能解的集合就叫做种群 ，比如在这个问题中设置100个这样的x , y 的可能的取值对，这100个个体就构成了种群。

编码、解码与染色体的概念

在上面个体概念里提到个体（也就是一组可能解）在计算机程序中被编码为一个向量表示，而在我们这个问题中，个体是x , y的取值，是两个实数，所以问题就可以转化为如何将实数编码为一个向量表示，可能有些朋友有疑惑，实数在计算机里不是可以直接存储吗，为什么需要编码呢？这里编码是为了后续操作（交叉和变异）的方便。实数如何编码为向量这个问题找了很多博客，写的都是很不清楚，看了莫烦python的教学代码，终于明白了一种实数编码、解码的方式。

生物的DNA有四种碱基对，分别是ACGT，DNA的编码可以看作是DNA上碱基对的不同排列，不同的排列使得基因的表现出来的性状也不同（如单眼皮双眼皮）。在计算机中，我们可以模仿这种编码，但是碱基对的种类只有两种，分别是0，1。只要我们能够将不同的实数表示成不同的0，1二进制串表示就完成了编码，也就是说其实我们并不需要去了解一个实数对应的二进制具体是多少，我们只需要保证有一个映射

$$y=f(x),xis decimal system,yis binary~system$$

能够将十进制的数编码为二进制即可，至于这个映射是什么，其实可以不必关心。将个体（可能解）编码后的二进制串叫做染色体，染色体（或者有人叫DNA）就是个体（可能解）的二进制编码表示。为什么可以不必关心映射$f ( x ) $呢？因为其实我们在程序中操纵的都是二进制串，而二进制串生成时可以随机生成，如：

#pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目,DNA_SIZE为编码长度，不理解乘2的看后文
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #matrix (POP_SIZE, DNA_SIZE*2)

实际上是没有需求需要将一个十进制数转化为一个二进制数，而在最后我们肯定要将编码后的二进制串转换为我们理解的十进制串，所以我们需要的是$y = f ( x )$的逆映射，也就是将二进制转化为十进制，这个过程叫做解码（很重要，感觉初学者不容易理解），理解了解码编码还难吗?先看具体的解码过程如下。

首先我们限制二进制串的长度为10（长度自己指定即可，越长精度越高），例如我们有一个二进制串（在程序中用数组存储即可）

$$[0,1,0,1,1,1,0,1,0,1]$$，这个二进制串如何转化为实数呢？不要忘记我们的$ x,y\in[-3,3]$这个限制，我们目标是求一个逆映射将这个二进制串映射到 $x,y\in[-3,3]$即可，为了更一般化我们将$x , y$的取值范围用一个变量表示，在程序中可以用python语言写到：

X_BOUND = [-3, 3] #x取值范围
Y_BOUND = [-3, 3] #y取值范围

为将二进制串映射到指定范围，首先先将二进制串按权展开，将二进制数转化为十进制数，我们有$02^9+12^8+02^7+…+02^0+1*2^0=373$，然后将转换后的实数压缩到$[0,1]$之间的一个小数， $373 / （2^{10}-1） \approx 0.36461388074$，通过以上这些步骤所有二进制串表示都可以转换为$[ 0 , 1 ] $之间的小数现在只需要将$[0,1] $ 区间内的数映射到我们要的区间即可。假设区间$[ 0 , 1 ]$内的数称为num，转换在python语言中可以写成：

#X_BOUND,Y_BOUND是x，y的取值范围 X_BOUND = [-3, 3], Y_BOUND = [-3, 3],
x_ = num * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0] #映射为x范围内的数
y_ = num * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0] #映射为y范围内的数

通过以上这些标记为蓝色的步骤我们完成了将一个二进制串映射到指定范围内的任务（解码）。

现在再来看看编码过程。不难看出上面我们的DNA（二进制串）长为10，10位二进制可以表示$2^{10}$种不同的状态，可以看成是将最后要转化为的十进制区间$x,y\in[-3,3]$（下面讨论都时转化到这个区间）切分成$ 2^{10}$份，显而易见，如果我们增加二进制串的长度，那么我们对区间的切分可以更加精细，转化后的十进制解也更加精确。例如，十位二进制全1按权展开为1023，最后映射到[-3, 3]区间时为3，而1111111110（前面9个1）按权展开为1022，$1022/(2^{10}-1) \approx 0.999022$，$ 0.999022*(3 - (-3)) + (-3)\approx2.994134$；如果我们将实数编码为12位二进制，111111111111（12个1）最后转化为3，而111111111110（前面11个1）按权展开为4094， $4094/(2^{12}-1=4095)\approx0.9997564094/(212−1=4095)≈0.999756$，$ 0.999755*(3-(-3))+(-3)\approx2.9985340.999755∗(3−(−3))+(−3)≈2.998534$;而 $3-2.994134=0.0058663−2.994134=0.005866$；$ 3-2.998534=0.0014663−2.998534=0.001466$，可以看出用10位二进制编码划分区间后，每个二进制状态改变对应的实数大约改变0.005866，而用12位二进制编码这个数字下降到0.001466，所以DNA长度越长，解码为10进制的实数越精确。

以下为解码过程的python代码：

这里我设置DNA_SIZE=24（一个实数DNA长度），两个实数$x , y$ 一共用48位二进制编码，我同时将x和y编码到同一个48位的二进制串里，每一个变量用24位表示，奇数24列为x的编码表示，偶数24列为y的编码表示。

def translateDNA(pop):#pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目
	x_pop = pop[:,1::2]#奇数列表示X
	y_pop = pop[:,::2] #偶数列表示y
    #pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)完成解码
    x = x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(X_BOUND[1]-X_BOUND[0])+X_BOUND[0]	
    y = y_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(Y_BOUND[1]-Y_BOUND[0])+Y_BOUND[0]
    return x,y

适应度和选择

我们已经得到了一个种群，现在要根据适者生存规则把优秀的个体保存下来，同时淘汰掉那些不适应环境的个体。现在摆在我们面前的问题是如何评价一个个体对环境的适应度？在我们的求最大值的问题中可以直接用可能解（个体）对应的函数的函数值的大小来评估，这样可能解对应的函数值越大越有可能被保留下来，以求解上面定义的函数F的最大值为例，python代码如下：

def get_fitness(pop): 
    x,y = translateDNA(pop)
	pred = F(x, y)
	return (pred - np.min(pred)) + 1e-3 #减去最小的适应度是为了防止适应度出现负数，通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度

pred是将可能解带入函数F中得到的预测值，因为后面的选择过程需要根据个体适应度确定每个个体被保留下来的概率，而概率不能是负值，所以减去预测中的最小值把适应度值的最小区间提升到从0开始，但是如果适应度为0，其对应的概率也为0，表示该个体不可能在选择中保留下来，这不符合算法思想，遗传算法不绝对否定谁也不绝对肯定谁，所以最后加上了一个很小的正数。

有了求最大值的适应度函数求最小值适应度函数也就容易了，python代码如下:

def get_fitness(pop): 
	x,y = translateDNA(pop)
	pred = F(x, y)
	return -(pred - np.max(pred)) + 1e-3

因为根据适者生存规则在求最小值问题上，函数值越小的可能解对应的适应度应该越大，同时适应度也不能为负值，先将适应度减去最大预测值，将适应度可能取值区间压缩为$[ n p . m i n ( p r e d ) − n p . m a x ( p r e d ) , 0 ]$，然后添加个负号将适应度变为正数，同理为了不出现0，最后在加上一个很小的正数。

有了评估的适应度函数，下面可以根据适者生存法则将优秀者保留下来了。选择则是根据新个体的适应度进行，但同时不意味着完全以适应度高低为导向（选择top k个适应度最高的个体，容易陷入局部最优解），因为单纯选择适应度高的个体将可能导致算法快速收敛到局部最优解而非全局最优解，我们称之为早熟。作为折中，遗传算法依据原则：适应度越高，被选择的机会越高，而适应度低的，被选择的机会就低。 在python中可以写做：

def select(pop, fitness):    # nature selection wrt pop's fitness
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=(fitness)/(fitness.sum()) )
    return pop[idx]

不熟悉numpy的朋友可以查阅一下这个函数，主要是使用了choice里的最后一个参数p，参数p描述了从np.arange(POP_SIZE)里选择每一个元素的概率，概率越高约有可能被选中，最后返回被选中的个体即可。

交叉、变异

通过选择我们得到了当前看来“还不错的基因”，但是这并不是最好的基因，我们需要通过繁殖后代（包含有交叉+变异过程）来产生比当前更好的基因，但是繁殖后代并不能保证每个后代个体的基因都比上一代优秀，这时需要继续通过选择过程来让试应环境的个体保留下来，从而完成进化，不断迭代上面这个过程种群中的个体就会一步一步地进化。

具体地繁殖后代过程包括交叉和变异两步。交叉是指每一个个体是由父亲和母亲两个个体繁殖产生，子代个体的DNA（二进制串）获得了一半父亲的DNA，一半母亲的DNA，但是这里的一半并不是真正的一半，这个位置叫做交配点，是随机产生的，可以是染色体的任意位置。通过交叉子代获得了一半来自父亲一半来自母亲的DNA，但是子代自身可能发生变异，使得其DNA即不来自父亲，也不来自母亲，在某个位置上发生随机改变，通常就是改变DNA的一个二进制位（0变到1，或者1变到0）。

需要说明的是交叉和变异不是必然发生，而是有一定概率发生。先考虑交叉，最坏情况，交叉产生的子代的DNA都比父代要差（这样算法有可能朝着优化的反方向进行，不收敛），如果交叉是有一定概率不发生，那么就能保证子代有一部分基因和当前这一代基因水平一样；而变异本质上是让算法跳出局部最优解，如果变异时常发生，或发生概率太大，那么算法到了最优解时还会不稳定。交叉概率，范围一般是0.6~1，突变常数（又称为变异概率），通常是0.1或者更小。

python实现如下

def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
	new_pop = []
	for father in pop:		#遍历种群中的每一个个体，将该个体作为父亲
		child = father		#孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
		if np.random.rand() < CROSSOVER_RATE:			#产生子代时不是必然发生交叉，而是以一定的概率发生交叉
			mother = pop[np.random.randint(POP_SIZE)]	#再种群中选择另一个个体，并将该个体作为母亲
			cross_points = np.random.randint(low=0, high=DNA_SIZE*2)	#随机产生交叉的点
			child[cross_points:] = mother[cross_points:]		#孩子得到位于交叉点后的母亲的基因
		mutation(child)	#每个后代有一定的机率发生变异
		new_pop.append(child)

	return new_pop

def mutation(child, MUTATION_RATE=0.003):
	if np.random.rand() < MUTATION_RATE: 				#以MUTATION_RATE的概率进行变异
		mutate_point = np.random.randint(0, DNA_SIZE)	#随机产生一个实数，代表要变异基因的位置
		child[mutate_point] = child[mutate_point]^1 	#将变异点的二进制为反转

上面这些步骤即为遗传算法的核心模块，将这些模块在主函数中迭代起来，让种群去进化

pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #生成种群 matrix (POP_SIZE, DNA_SIZE)
for _ in range(N_GENERATIONS):	#种群迭代进化N_GENERATIONS代
	crossover_and_mutation(pop, CROSSOVER_RATE)	#种群通过交叉变异产生后代
	fitness = get_fitness(pop)	#对种群中的每个个体进行评估
	pop = select(pop, fitness) 	#选择生成新的种群

完整代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

DNA_SIZE = 24
POP_SIZE = 200
CROSSOVER_RATE = 0.8
MUTATION_RATE = 0.005
N_GENERATIONS = 50
X_BOUND = [-3, 3]
Y_BOUND = [-3, 3]


def F(x, y):
	return 3*(1-x)**2*np.exp(-(x**2)-(y+1)**2)- 10*(x/5 - x**3 - y**5)*np.exp(-x**2-y**2)- 1/3**np.exp(-(x+1)**2 - y**2)

def plot_3d(ax):

	X = np.linspace(*X_BOUND, 100)
	Y = np.linspace(*Y_BOUND, 100)
	X,Y = np.meshgrid(X, Y)
	Z = F(X, Y)
	ax.plot_surface(X,Y,Z,rstride=1,cstride=1,cmap=cm.coolwarm)
	ax.set_zlim(-10,10)
	ax.set_xlabel('x')
	ax.set_ylabel('y')
	ax.set_zlabel('z')
	plt.pause(3)
	plt.show()


def get_fitness(pop): 
    x,y = translateDNA(pop)
	pred = F(x, y)
	return (pred - np.min(pred)) + 1e-3 #减去最小的适应度是为了防止适应度出现负数，通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)],最后在加上一个很小的数防止出现为0的适应度


def translateDNA(pop): #pop表示种群矩阵，一行表示一个二进制编码表示的DNA，矩阵的行数为种群数目
	x_pop = pop[:,1::2]#奇数列表示X
	y_pop = pop[:,::2] #偶数列表示y
	
	#pop:(POP_SIZE,DNA_SIZE)*(DNA_SIZE,1) --> (POP_SIZE,1)
	x = x_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(X_BOUND[1]-X_BOUND[0])+X_BOUND[0]
	y = y_pop.dot(2**np.arange(DNA_SIZE)[::-1])/float(2**DNA_SIZE-1)*(Y_BOUND[1]-Y_BOUND[0])+Y_BOUND[0]
	return x,y

def crossover_and_mutation(pop, CROSSOVER_RATE = 0.8):
	new_pop = []
	for father in pop:		#遍历种群中的每一个个体，将该个体作为父亲
		child = father		#孩子先得到父亲的全部基因（这里我把一串二进制串的那些0，1称为基因）
		if np.random.rand() < CROSSOVER_RATE:			#产生子代时不是必然发生交叉，而是以一定的概率发生交叉
			mother = pop[np.random.randint(POP_SIZE)]	#再种群中选择另一个个体，并将该个体作为母亲
			cross_points = np.random.randint(low=0, high=DNA_SIZE*2)	#随机产生交叉的点
			child[cross_points:] = mother[cross_points:]		#孩子得到位于交叉点后的母亲的基因
		mutation(child)	#每个后代有一定的机率发生变异
		new_pop.append(child)

	return new_pop

def mutation(child, MUTATION_RATE=0.003):
	if np.random.rand() < MUTATION_RATE: 				#以MUTATION_RATE的概率进行变异
		mutate_point = np.random.randint(0, DNA_SIZE*2)	#随机产生一个实数，代表要变异基因的位置
		child[mutate_point] = child[mutate_point]^1 	#将变异点的二进制为反转

def select(pop, fitness):    # nature selection wrt pop's fitness
    idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
                           p=(fitness)/(fitness.sum()) )
    return pop[idx]

def print_info(pop):
	fitness = get_fitness(pop)
	max_fitness_index = np.argmax(fitness)
	print("max_fitness:", fitness[max_fitness_index])
	x,y = translateDNA(pop)
	print("最优的基因型：", pop[max_fitness_index])
	print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))


if __name__ == "__main__":
	fig = plt.figure()
	ax = Axes3D(fig)	
	plt.ion()#将画图模式改为交互模式，程序遇到plt.show不会暂停，而是继续执行
	plot_3d(ax)

	pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE*2)) #matrix (POP_SIZE, DNA_SIZE)
	for _ in range(N_GENERATIONS):#迭代N代
		x,y = translateDNA(pop)
		if 'sca' in locals(): 
			sca.remove()
		sca = ax.scatter(x, y, F(x,y), c='black', marker='o');plt.show();plt.pause(0.1)
		pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
		#F_values = F(translateDNA(pop)[0], translateDNA(pop)[1])#x, y --> Z matrix
		fitness = get_fitness(pop)
		pop = select(pop, fitness) #选择生成新的种群
	
	print_info(pop)
	plt.ioff()
	plot_3d(ax)

后记：很多人评论最后最大适应度很小是不是没收敛，我说一下我的理解，请注意最大适应度和F(x,y)不等价，最大适应度小不能说明没有拟合，认真观察适应度咋算的，是F(x,y) - min(F(x,y))，这个值小，F(x,y)的最大值和最小值很接近，方差很小，反而可能是表明收敛了

Microbial Genetic Algorithm

原文章：莫烦Python

说到遗传算法 (GA), 有一点不得不提的是如何有效保留好的父母 (Elitism), 让好的父母不会消失掉. 这也是永远都给自己留条后路的意思. Microbial GA (后面统称 MGA) 就是一个很好的保留 Elitism 的算法. 一句话来概括: 在袋子里抽两个球, 对比两个球, 把球大的放回袋子里, 把球小的变一下再放回袋子里, 这样在这次选着中, 大球不会被改变任何东西, 就被放回了袋子, 当作下一代的一部分.

算法

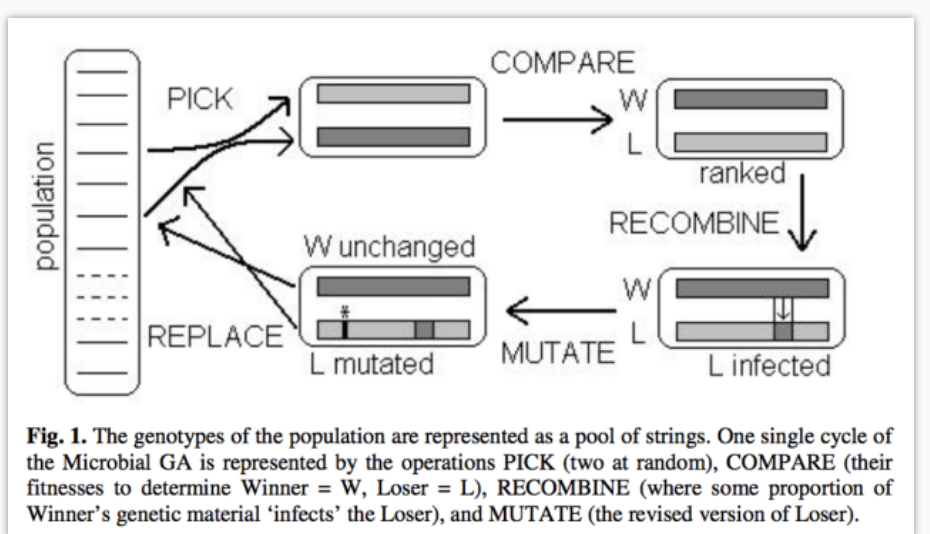
像最开始说的那样, 我们有一些 population, 每次在进化的时候, 我们会从这个 pop 中随机抽 2 个 DNA 出来, 然后对比一下他们的 fitness, 我们将 fitness 高的定义成 winner, 反之是 loser. 我们不会去动任何 winner 的 DNA, 要动手脚的只有这个 loser, 比如对 loser 进行 crossover 和 mutate. 动完手脚后将 winner 和 loser 一同放回 pop 中.

通过这样的流程, 我们就不用担心有时候变异着变异着, 那些原本好的 pop 流失掉了, 有了这个 MGA 算法, winner 总是会被保留下来的. GA 中的 Elitism 问题通过这种方法巧妙解决了.

什么是进化策略 (Evolution Strategy)

遗传算法和进化策略共享着一些东西. 他们都用遗传信息, 比如 DNA 染色体, 一代代传承, 变异. 来获取上一代没有的东西.然后通过适者生存, 不适者淘汰的这一套理论不断进化着. 我们的祖先, 通过不断变异, 生存淘汰, 从猴子变成人也就是这么回事.既然进化策略或遗传算法都用到了进化的原则, 他们到底有哪些不同呢? 他们各自又适用于哪些问题呢?

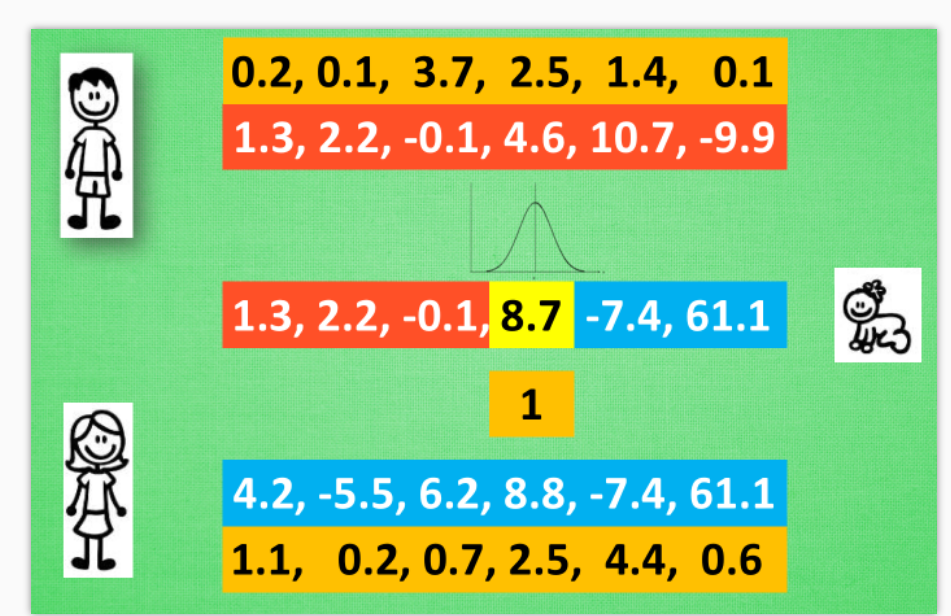
爸妈的 DNA 不用再是 01 的这种形式, 我们可以用实数来代替, 咋一看, 觉得牛逼了起来, 因为我们抛开了二进制的转换问题, 从而能解决实际生活中的很多由实数组成的真实问题. 比如我有一个关于 x 的公式, 而这个公式中其他参数, 我都能用 DNA 中的实数代替, 然后进化我的 DNA, 也就是优化这个公式啦. 这样用起来, 的确比遗传算法方便. 同样, 在制造宝宝的时候, 我们也能用到交叉配对, 一部分来自爸爸, 一部分来自妈妈. 可是我们应该如何变异呢? 遗传算法中简单的翻牌做法貌似在这里行不通. 不过进化策略中的另外一个因素起了决定性的作用. 这就是变异强度. 简单来说, 我们将爸妈遗传下来的值看做是正态分布的平均值, 再在这个平均值上附加一个标准差, 我们就能用正态分布产生一个相近的数了. 比如在这个8.8位置上的变异强度为1, 我们就按照1的标准差和8.8的均值产生一个离8.8的比较近的数, 比如8.7. 然后对宝宝每一位上的值进行同样的操作. 就能产生稍微不同的宝宝 DNA 啦. 所以, 变异强度也可以被当成一组遗传信息从爸妈的 DNA 里遗传下来. 甚至遗传给宝宝的变异强度基因也能变异. 进化策略的玩法也能多种多样.

我们总结一下, 在进化策略中, 可以有两种遗传性系被继承给后代, 一种是记录所有位置的均值, 一种是记录这个均值的变异强度, 有了这套体系, 我们就能更加轻松自在的在实数区间上进行变异了. 这种思路甚至还能被用在神经网络的参数优化上, 因为这些参数本来就是一些实数. 在之后的视频中我们会继续提到当今比较流行的将人工神经网络结合上遗传算法或者进化策略的方法.

（1+1）ES

像上面看到的, 统一来说都是 (μ/ρ +, λ)-ES, (1+1)-ES 只是一种特殊形式. 这里的 μ 是 population 的数量, ρ 是从 population 中选取的个数, 用来生成宝宝的. λ 是生成的宝宝数, 如果采用的是 + 形式的, 就是使用将 ρ + λ 混合起来进行适者生存, 如果是 , 形式, 那么就是只使用 λ 进行适者生存.

形式多种多样有些头疼. 不过在这一节中, 我们考虑的只是一个爸爸, 生成一个宝宝, 然后在爸爸和宝宝中进行适者生存的游戏, 选择爸爸和宝宝中比较好的那个当做下一代的爸爸. (1+1)-ES 总结如下:

• 有一个爸爸;
• 根据爸爸变异出一个宝宝;
• 在爸爸和宝宝中选好的那个变成下一代爸爸.

Natural Evolution Strategy

NES 的方法其实和强化学习中 Policy Gradient 的方法非常接近. 简单来概括一下它们的不同: 在行为的策略上, PG 是扰动 Action, 不同的 action 带来不同的 reward, 通过 reward 大小对应上 action 来计算 gradient, 再反向传递 gradient. 但是 ES 是扰动 神经网络中的 Parameters, 不同的 parameters 带来不同的 reward, 通过 reward 大小对应上 parameters 来按比例更新原始的 parameters.

蚁群算法 (Ant Colony Optimization, ACO)

1991 年，意大利学者 Dorigo M. 等人在第一届欧洲人工生命会议 (ECAL) 上首次提出了蚁群算法。1996 年 Dorigo M. 等人发表的文章 “Ant system: optimization by a colony of cooperating agents”为蚁群算法奠定了基础。在自然界中，蚂蚁会分泌一种叫做信息素的化学物质，蚂蚁的许多行为受信息素的调控。蚂蚁在运动过程中能够感知其经过的路径上信息素的浓度，蚂蚁倾向朝着信息素浓度高的方向移动。以下图为例：

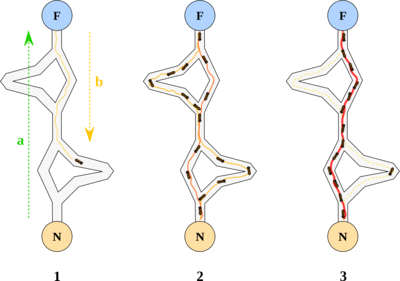
蚂蚁从蚁巢 (N) 出发到达食物源所在地 (F)，取得食物后再折返回蚁巢。整个过程中蚂蚁有多种路径可以选择，单位时间内路径上通过蚂蚁的数量越多，则该路径上留下的信息素浓度越高。因此，最短路径上走过的蚂蚁数量越多，则后来的蚂蚁选择该路径的机率就越大，从而蚂蚁通过信息的交流实现了寻找食物和蚁巢之间最短路的目的。

粒子群算法 (Particle Swarm Optimization, PSO)

Eberhart, R. 和 Kennedy, J. 于 1995 年提出了粒子群优化算法。粒子群算法模仿的是自然界中鸟群和鱼群等群体的行为，其基本原理描述如下：

一个由 $m$个粒子 (Particle) 组成的群体 (Swarm) 在 $D$维空间中飞行，每个粒子在搜索时，考虑自己历史搜索到的最优解和群体内 (或邻域内) 其他粒子历史搜索到的最优解，在此基础上进行位置 (状态，也就是解) 的变化。令第 $i$个粒子的位置为 $x_i$，速度为 $v_i$，历史搜索的最优解对应的点为 $p_i$，群体内 (或邻域内) 所有粒子历史搜索到的最优解对应的点为 $p_g$，则粒子的位置和速度依据如下公式进行变化：
$$
\begin{array}{ll}&v_{i}^{k+1}=\omega v_{i}^{k}+c_{1}\xi\left(p_{i}^{k}-x_{i}^{k}\right)+c_{2}\eta\left(p_{g}^k-x_{i}^k\right)\ &x_{i}^{k+2}=x_{i}^{k}+v^{k+1}{i}\ \end{array}
$$
其中，$\omega$为惯性参数；$c_1$ 和 $c_2$ 为学习因子，其一般为正数，通常情况下等于 2；$\xi$,$\eta$∈$U[0,1]$。学习因子使得粒子具有自我总结和向群体中优秀个体学习的能力，从而向自己的历史最优点以及群体内或邻域内的最优点靠近。同时，粒子的速度被限制在一个最大速度 $V{max}$范围内。

对于 $Rosenbrock $函数
$$
f \left(x, y\right) = \left(1 - x\right)^2 + 100 \left(y - x^2\right)^2
$$
当$x \in \left[-2, 2\right], y \in \left[-1, 3\right]$，定义优化问题为最小化目标函数，最优解为 (0,0)。利用 PySwarms 扩展包的优化过程可视化如下

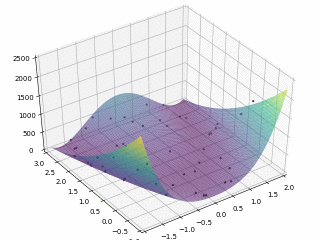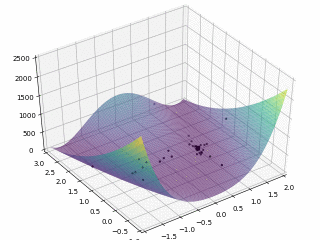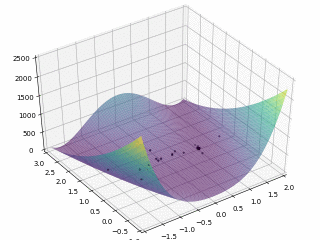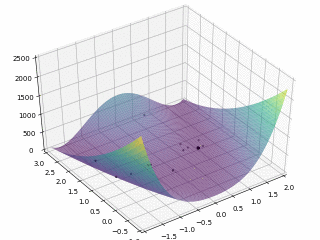
其中，$m = 50, \omega = 0.8, c_1 = 0.5, c_2 = 0.3$，迭代次数为 $200$

本节相关示例代码详见 这里。

超启发式算法 (Hyper-Heuristic Algorithms)

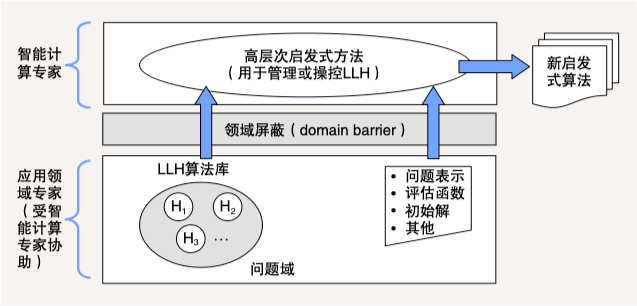
超启发式算法 (Hyper-Heuristic Algorithms) 提供了一种高层次启发式方法，通过管理或操纵一系列低层次启发式算法 (Low-Level Heuristics，LLH)，以产生新的启发式算法。这些新启发式算法被用于求解各类组合优化问题 12。

下图给出了超启发式算法的概念模型。该模型分为两个层面：在问题域层面上，应用领域专家根据自己的背景知识，在智能计算专家协助下，提供一系列 LLH 和问题的定义、评估函数等信息；在高层次启发式方法层面上，智能计算专家设计高效的管理操纵机制，运用问题域所提供的 LLH 算法库和问题特征信息，构造出新的启发式算法。