一、从损失函数公式本身来说
1. 从损失函数公式的物理含义来说
MSE衡量的是预测值和目标值的欧式距离。
而交叉熵是一个信息论的概念,交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
所以交叉熵本质上是概率问题,表征真实概率分布与预测概率分布差异,和几何上的欧氏距离无关,在回归中才有欧氏距离的说法,
而在分类问题中label的值大小在欧氏空间中是没有意义的。所以分类问题不能用mse作为损失函数。
2. 强行使用的话,可能带来的后果
MSE(均方误差)对于每一个输出的结果都非常看重(让正确分类变大的同时,也让错误分类变得平均),而交叉熵只对正确分类的结果看重。
例如:在一个三分类模型中,模型的输出结果为(a,b,c),而真实的输出结果为(1,0,0),那么MSE与cross-entropy相对应的损失函数的值如下:
MSE:
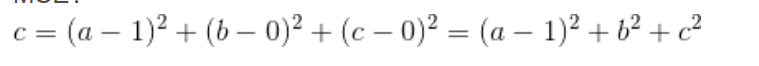
cross-entropy:
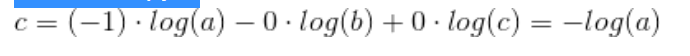
从上述的公式可以看出,交叉熵的损失函数只和分类正确的预测结果有关系,而MSE的损失函数还和错误的分类有关系,该分类函数除了让正确的分类尽量变大,还会让错误的分类变得平均,但实际在分类问题中这个调整是没有必要的。但是对于回归问题来说,这样的考虑就显得很重要了。所以,回归问题熵使用交叉上并不合适。
二、从优化求解角度来说
1. 非凸有多个极值点,不合适做损失函数
分类问题是逻辑回归,必须有激活函数这个非线性单元在,比如sigmoid(也可以是其他非线性激活函数),而如果还用mse做损失函数的话:
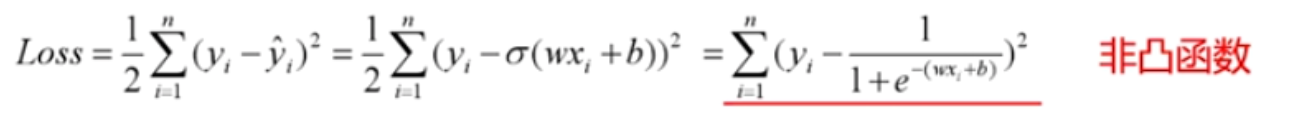
mse已经是非凸函数了,有多个极值点,所以不适用做损失函数了。
2.求解过程中可能梯度消失(不是主要原因)
mse作为损失函数,求导的时候都会有对激活函数的求导连乘运算,对于sigmoid、tanh,有很大区域导数为0的。
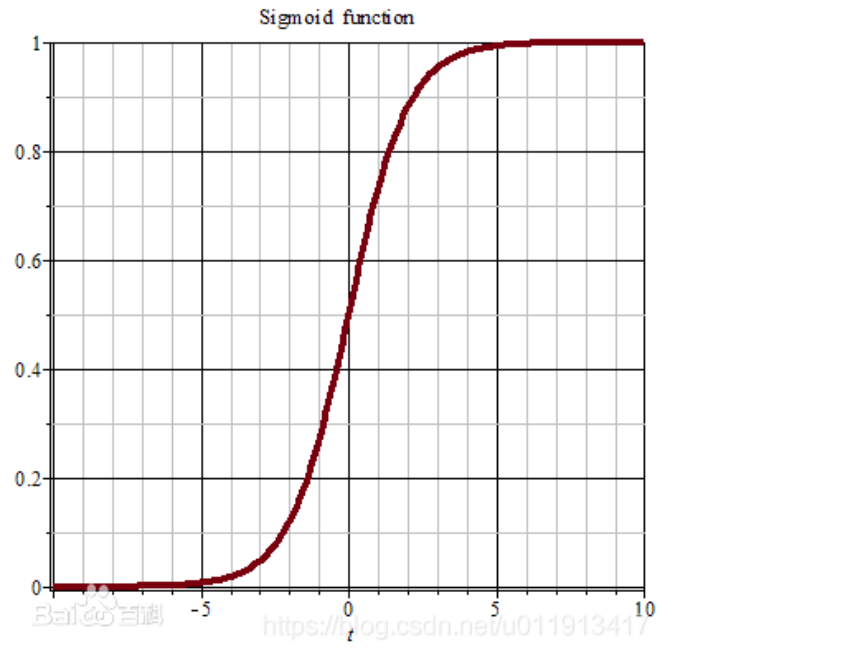
该激活函数的输入很可能直接就在平坦区域,那么导数就几乎是0,梯度就几乎不会被反向传递,梯度直接消失了。所以mse做损失函数的时候最后一层不能用sigmoid做激活函数,其他层可以用sigmoid做激活函数。
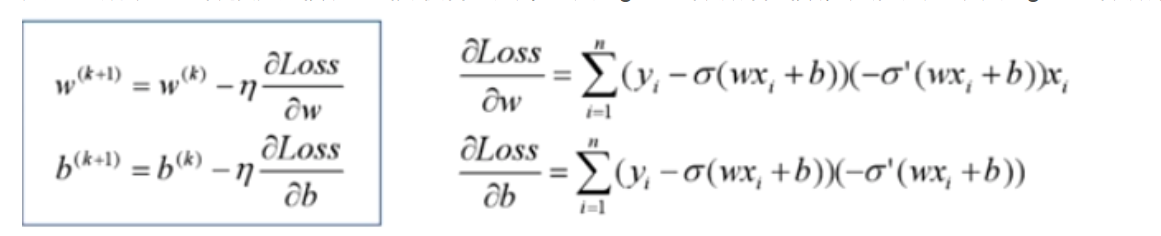
当然,用其他损失函数只能保证在第一步不会直接死掉,反向传播如果激活函数和归一化做得不好,同样会梯度消失。所以从梯度这个原因说mse不好不是很正确。

