课程地址:跳转
系列十——EM算法
给出EM公式,解释E步,M步以及收敛性证明

EM算法的推导(公式是怎么来的)
ELBO + KL divergence(kL >= 0)
先固定$\theta$,然后求期望(E),再滑动$\theta$ 使得期望值最大(M)
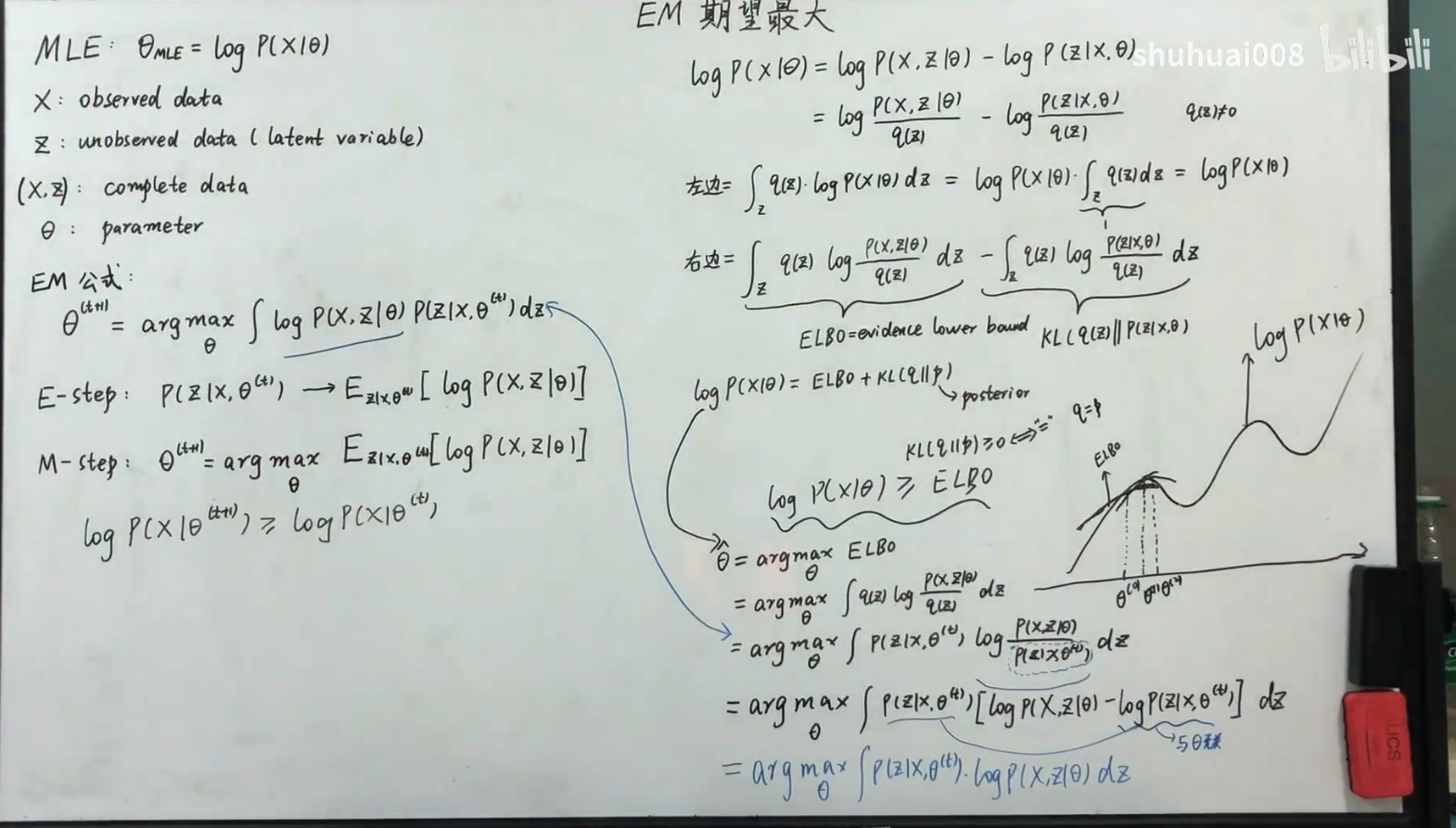
ELBO + Jensen’s Inequality

以上两种证明方法得出的结果一样。
EM是一种算法
从狭义EM到广义EM
概率生成模型
EM算法用于解决具有隐变量的混合模型的极大似然估计问题
不知道P(x)的分布,无法直接求解,所以我们引入归纳偏置,即假定服从某个参数模型


$\log(x|\theta)=ELBO+KL(q||p)$
- 固定$\theta$,$x$为观测值,即$log(x|\theta)$固定,这时,$q$越接近与$p$,那么$ELBO$越大,即$\hat{q}=argmin(KL(q||p))=argmax(ELBO)$ 【E-step】
- 固定$\hat{q}, \ \ \ \theta=argmax_{\theta}ELPO$【M-step】

以上过程称为广义EM,E步和M步交替进行。即

引出广义EM,原始的EM公式是广义EM的一种特殊情况

EM算法给出一个求解的框架,理想状况下,后验可以一步到位求出,实际中可能会有问题。这时我们可以用变分推断或者蒙特卡洛采样的方法。这就产生了两个变种

VI (variational inference)= VB(variational bayes)
VBEM(VEM)——EM变种
MCEM——EM变种

系列十一——高斯混合模型
混合模型一般都是生成模型
GMM的两种视角
从几何角度来说,就是高斯分布的加权平均,从生成模型角度来说,引入隐变量$z$来表示所属于哪个高斯分布。
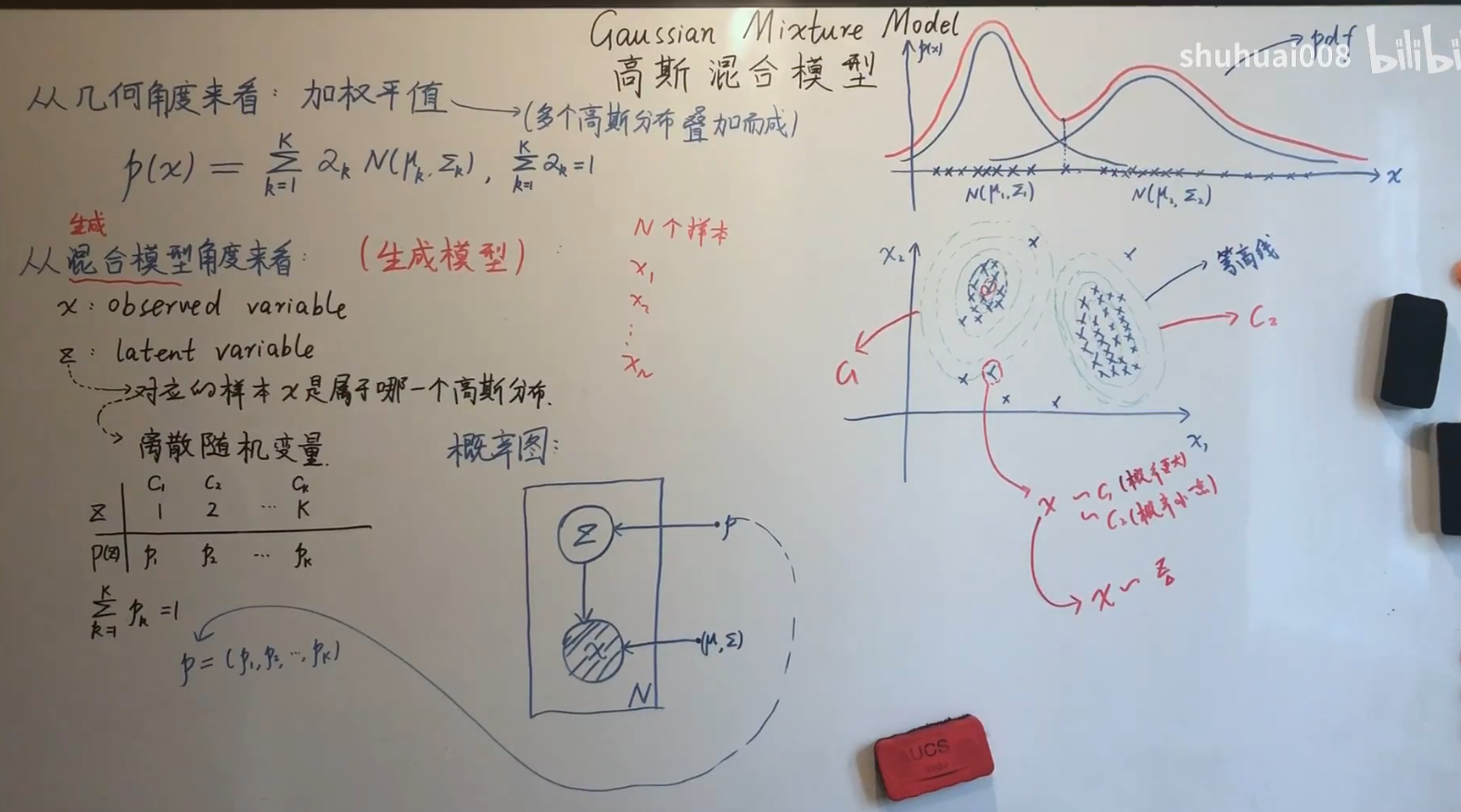
硬分类和软分类
在分类中,为数据分配为唯一的类别,这样称之为硬分类(Crisp Classification)(像是0,1分类);而对应的称之为软分类(Soft Classification),每个数据都可能被分配多个可能的类别(依据概率值)。
用MLE无法求的解析解,log里面是连加,无法分离,对于高维变量,求偏导令其为0无法求得。可以用数值迭代的方法

E-step

M-step


系列十二——变分推断
背景目的


公式推导
基于平均场理论


统一符号规范,平均场理论的强假设存在很大的问题(不能保证划分的z之间相互独立),不适合于大部分模型(比如说神经网络此方法就失效了)


SGVI
写出梯度,并把它等价的变换成期望的形式,这样就可以通过蒙特卡洛采样的方法估计出梯度,然后进行梯度上升。
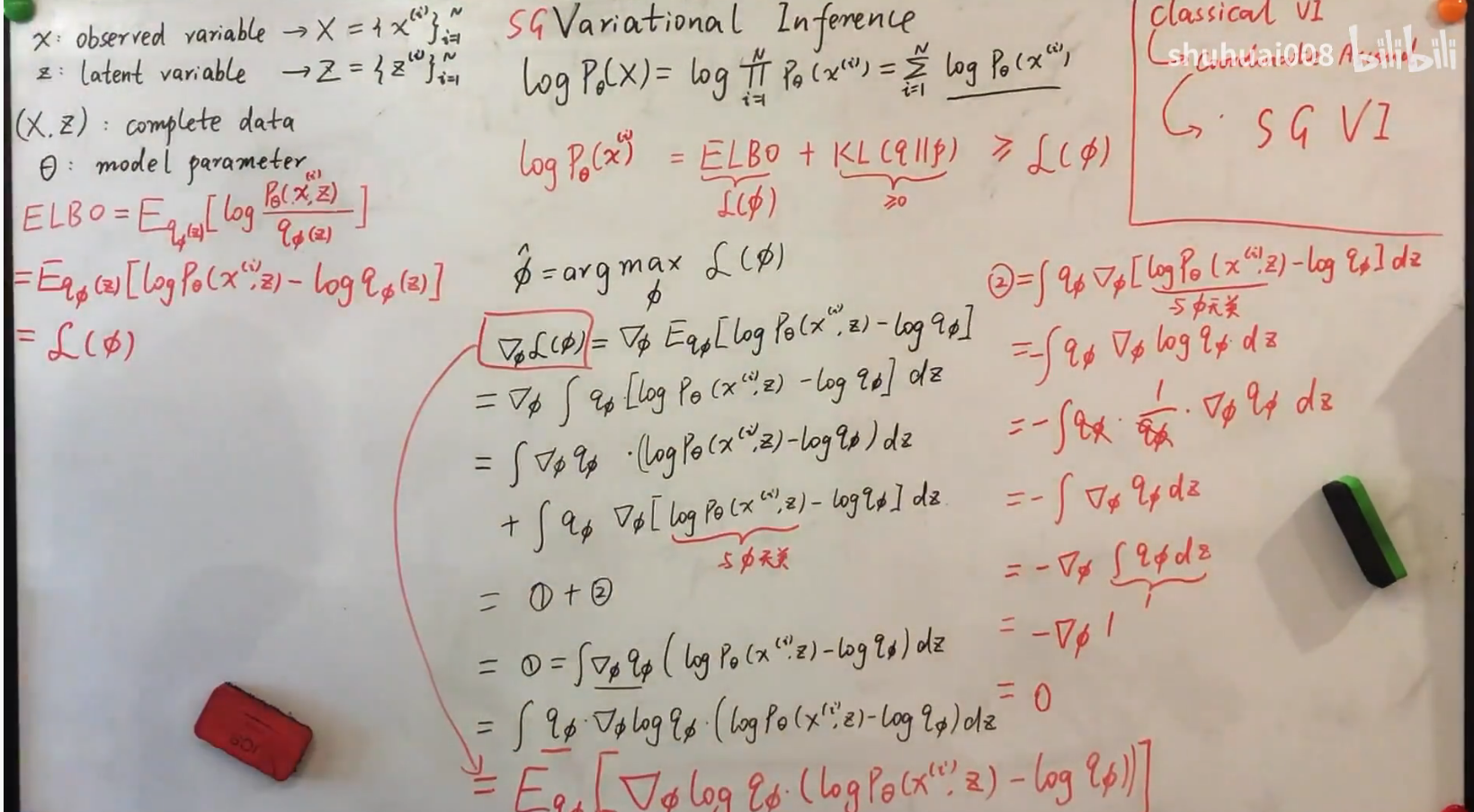
因为log函数的特殊性(接近0时趋于无穷),会造成蒙特卡洛采样采样的数据方差非常大,因此需要非常多的样本才行(实际中可能不可行)

为了解决high variance的问题,引入重参数化技巧(没看懂。。o(╥﹏╥)o)



