正定/负定、半正定/半负定


方程有解判定
对于齐次线性方程组来说一定有解;
对于非齐次:

数字特征
协方差
在概率论和统计学中,协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况,即当两个变量是相同的情况。
期望值分别为E[X]与E[Y]的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为:
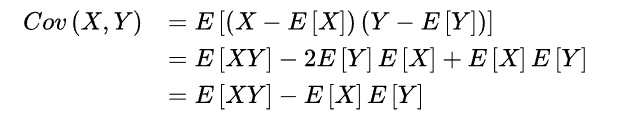
从直观上来看,协方差表示的是两个变量总体误差的期望。
如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值;如果两个变量的变化趋势相反,即其中一个变量大于自身的期望值时另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
如果X与Y是统计独立的,那么二者之间的协方差就是0,因为两个独立的随机变量满足E[XY]=E[X]E[Y]。
但是,反过来并不成立。即如果X与Y的协方差为0,二者并不一定是统计独立的。
协方差Cov(X,Y)的度量单位是X的协方差乘以Y的协方差。
协方差为0的两个随机变量称为是不相关的。
基变换


如何用Je的语言描述向量的变换呢,我们先坐成一个A(用我们的坐标描述Je的基向量),然后用我们的话描述向量的变化(比如向左旋转90度),最后再乘以$A^{-1}$就转化为用她的语言去描述变换矩阵了。

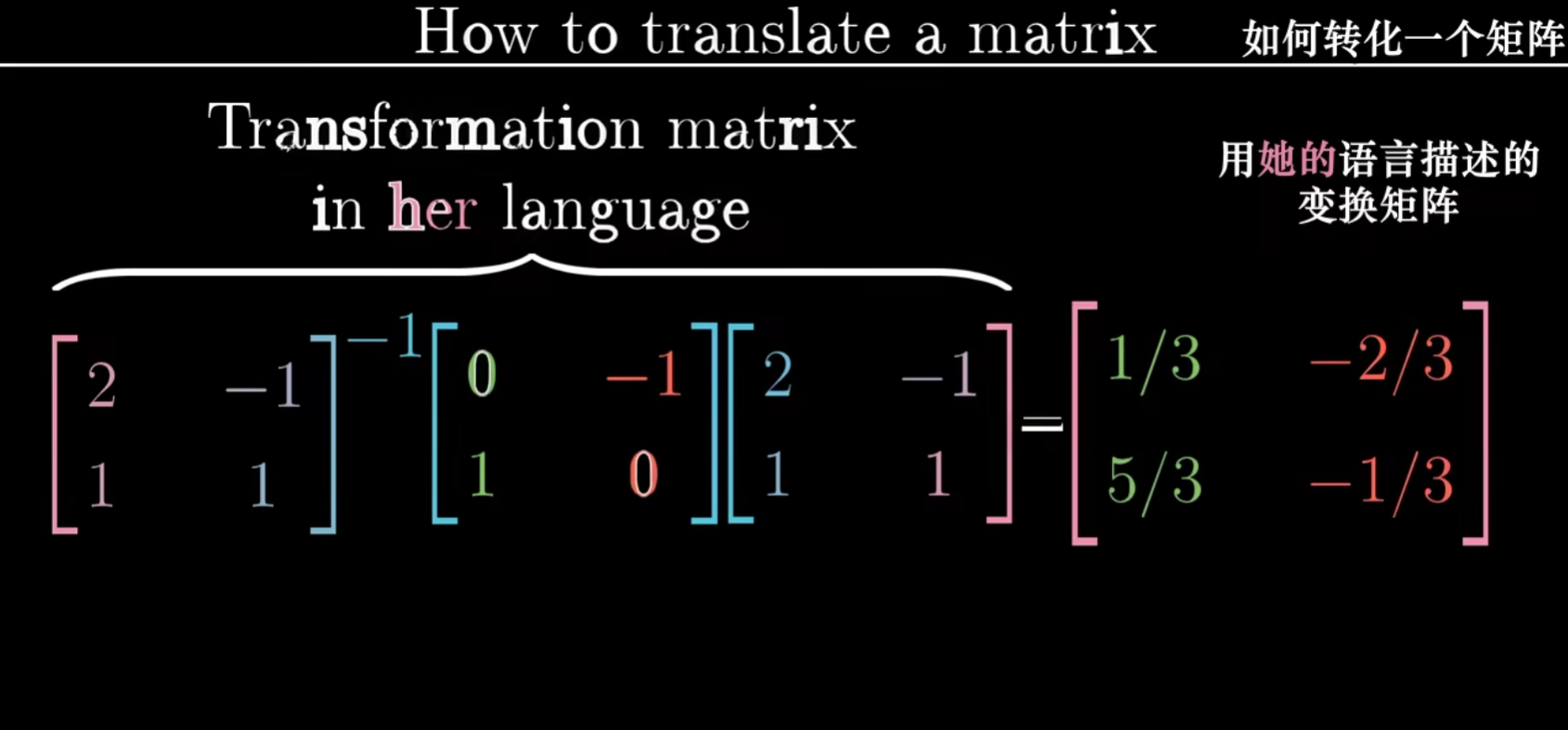
$A^{-1}MA$暗示一种数学上的转移作用,中间的矩阵$M$代表一种标准坐标系下常见的的变换(旋转变换,剪切变换等);$A^{-1},A$代表转移作用 ,也就是在不同于标准坐标系与标准坐标系之间进行转换, 实际上也是视角上的转化。矩阵乘积代表着同一种变换,只不过是从别的坐标系的角度来看。

