常见不等式放缩
一: 一些重要恒等式
ⅰ:$1^2+2^2+…+n^2=\frac{n(n+1)(2n+1)}{6}$
ⅱ:$ 1^3+2^3+…+n^3=(1+2+…+n)^2 $
Ⅲ:$cosa+cos2a+…+cos2^na=\frac{sin2^{n+1}a}{2^{n+1}sina}$
二 重要不等式
1**:绝对值不等式**
$︱︱x︱-︱y︱︱≤∣x±y∣≤︱x︱+︱y︱(别看简单,常用)$
2:伯努利不等式
$(1+x)^n≥1+nx (x>-1)$

3:柯西不等式
$ (∑ a_i b_i)^2≤∑a_i^2∑b_i^2$
4:
$︱sin nx︱≤n︱sin x︱$
5;
$(a+b)^p≤2^pmax(︱a^p︱,︱b^p︱)$
$(a+b)^p≤a^p+ b^p (0<p<1) $
$(a+b)^p≥a^p+ b^p (p>1) $
6:
7:切比雪夫不等式
$若a1≤a2≤…≤an, b1≤b2≤…≤bn$
$∑a_ib_i≥(1/n)∑a_i∑b_i$
$若a1≤a2≤…≤an, b1≥b2≥…≥bn$
$∑aibi≤(1/n)∑ai∑bi$
8.均值不等式

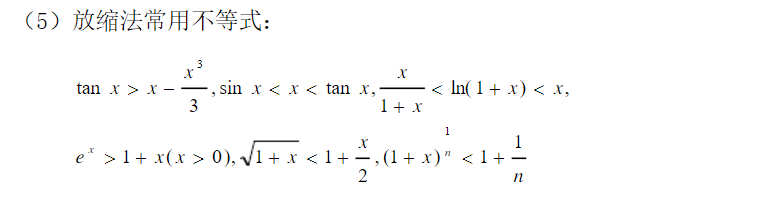
一些常见公式
方差公式
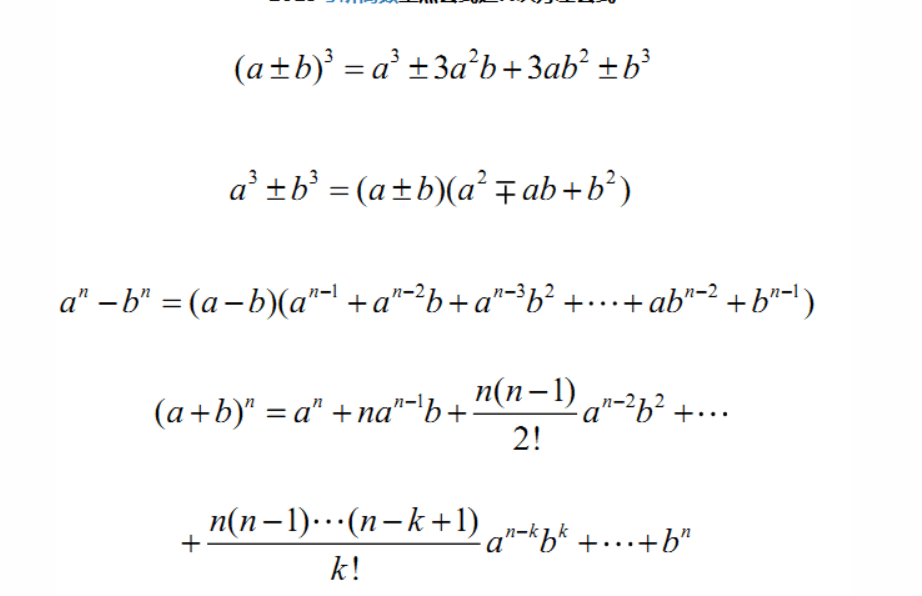
等比等差
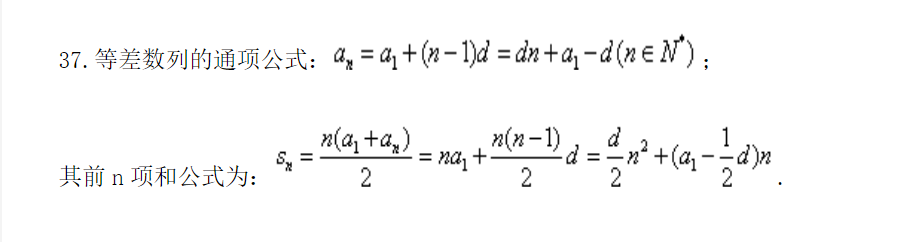
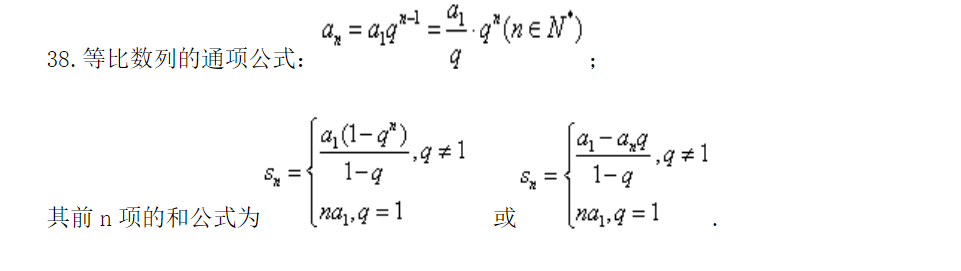
三角函数
已知sin(π/2-y)=cosy
设sin(π/2-y)=x,则cosy=x
则arcsinx=π/2-y,arccosx=y,所以得两者相加为π/2
sin(-α)=-sinα
cos(-α)=cosα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
sin(π-α)=sinα
cos(π-α)=-cosα
sin(π+α)=-sinα
tanα=sinα/cosα
tan(π/2+α)=-cotα
tan(π/2-α)=cotα
tan(π-α)=-tanα
tan(π+α)=tanα
倍角公式
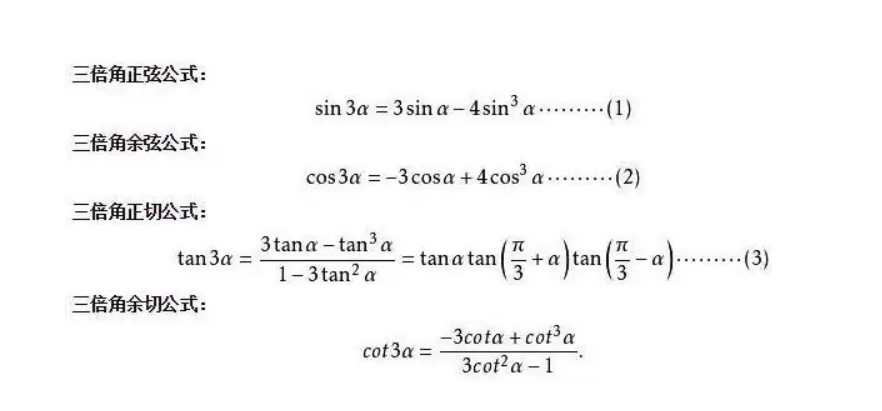
二项式定理
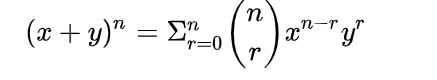
排列组合公式
组合数公式


排列数公式
计数问题
相邻问题–捆绑法
具体解题步骤如下:
①看到“相邻”、“在一起”等类似字眼,就想到用捆绑法;
②将相邻元素看成一个整体和其他元素进行排列;
③思考相邻元素需不需要进行内部交换,若交换相邻元素的位置对结果造成影响就必须考虑交换,如无影响就不需要交换。
问题1.
最近火爆的电视剧《人世间》中,一家五口人想去约着拍照
但是,老三就想和妈妈挨着
一家之主的爸爸让考入北大的老大算算有几种排列方法
老大很快算出了最后的结果。
老三很是惊讶,去请教老大。
老大解释道:若题干中看到“相邻”元素时,就把相邻元素捆绑在一起,把他们看成一个整体,当和其他元素排列时,不能分开。
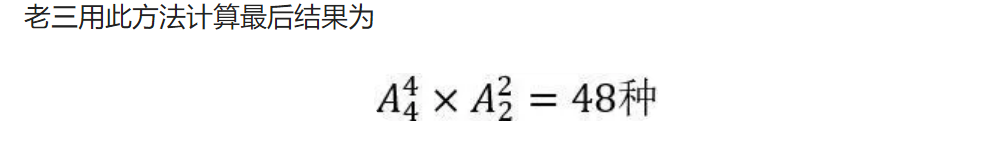
定序问题–除法
对于某几个元素顺序一定的排列问题,可先将这几个元素与其它元素一同进行排列,然后用总的排列数除以这几个元素的全排列数.
例题:
有4名男生,3名女生。3名女生高矮互不等,将7名学生排成一行,要求从左到右,女生从矮到高排列,有多少种排法?

其他
$(\sqrt[n]{x})^m=\sqrt[n]{x^m}$
几何
点到直线距离公式

理论知识
光滑曲线的含义:处处存在导数且曲线连续,处处可导
2.数域符号


