《吴恩达机器学习笔记》
第一节
关于不知道如何编写无人驾驶直升机的算法程序,让机器自己学习去解决。机器学习的定义

经验E,性能度量P,任务T
在跳棋程序自我学习时,E是数百万次的下棋训练,P是程序赢的概率,T是进行下棋
主要的两类学习算法
- 监督学习(supervised learning):告诉你正确答案,让你设计算法预测
- 分类问题(classification problem)- - 预测离散值的输出
- 回归问题(regression problem)- - 预测连续值的输出
- 无监督学习(unsupervised learning):
- 聚类算法(clustering algorithm)例如百度谷歌新闻,用此来聚集相关主题的新闻
- 监督学习(supervised learning):告诉你正确答案,让你设计算法预测
第二节
一些有用的符号
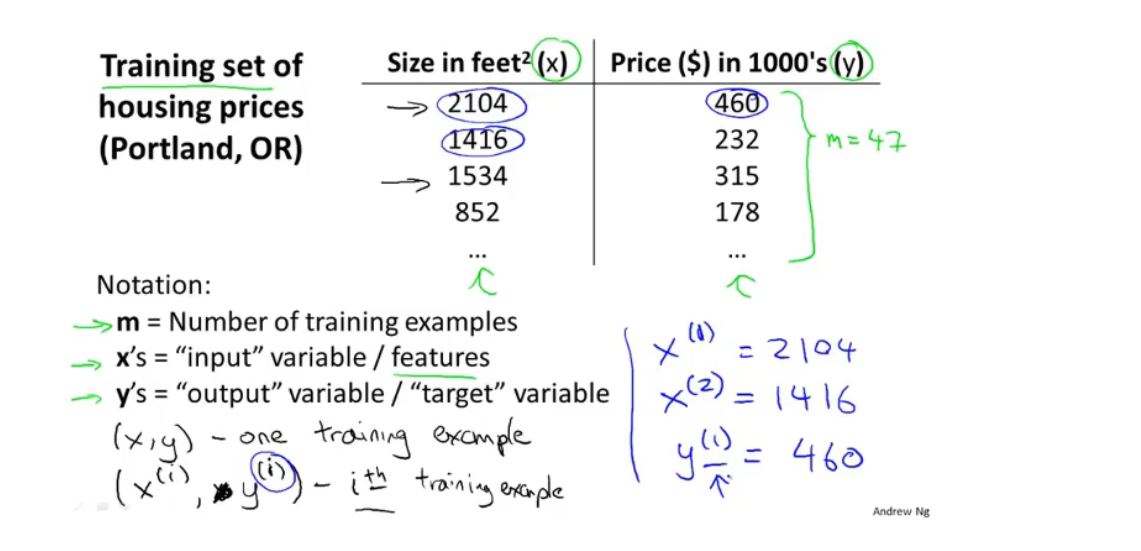
监督学习流程
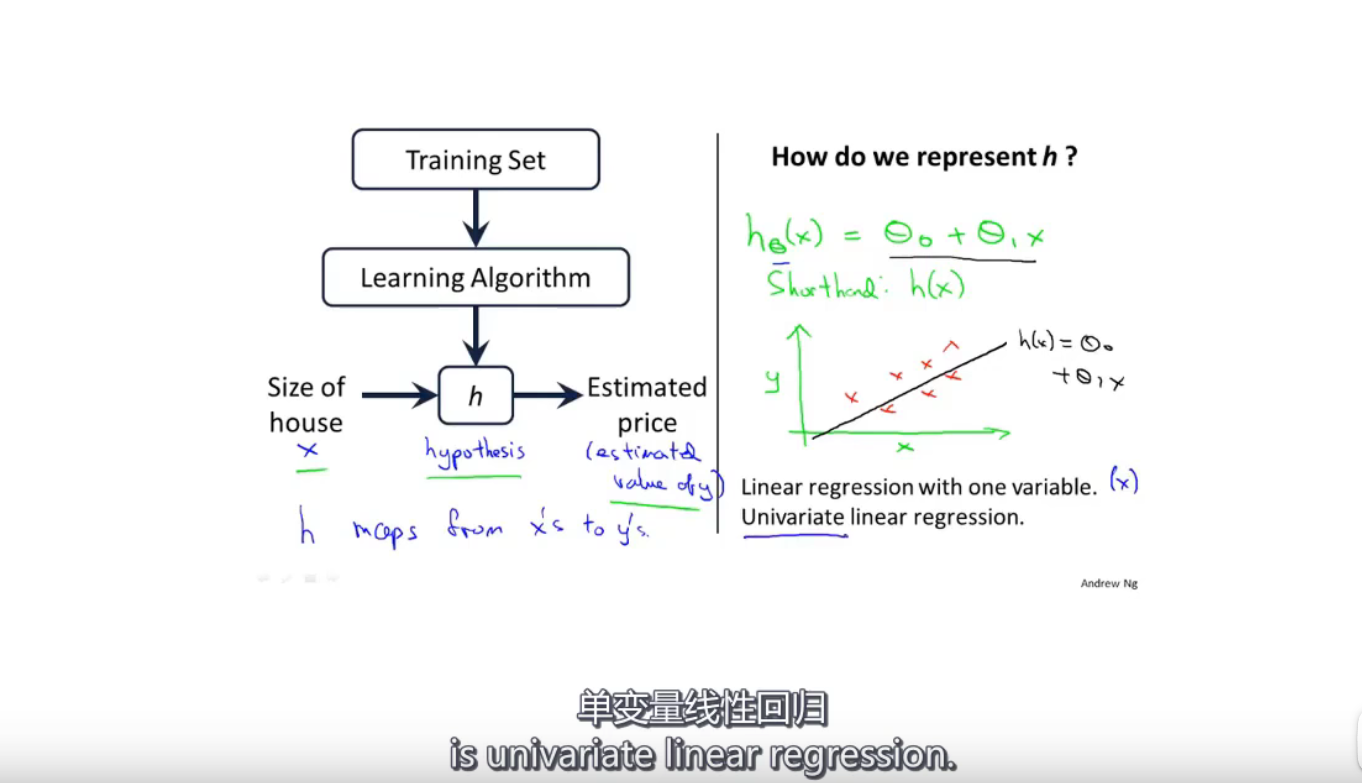
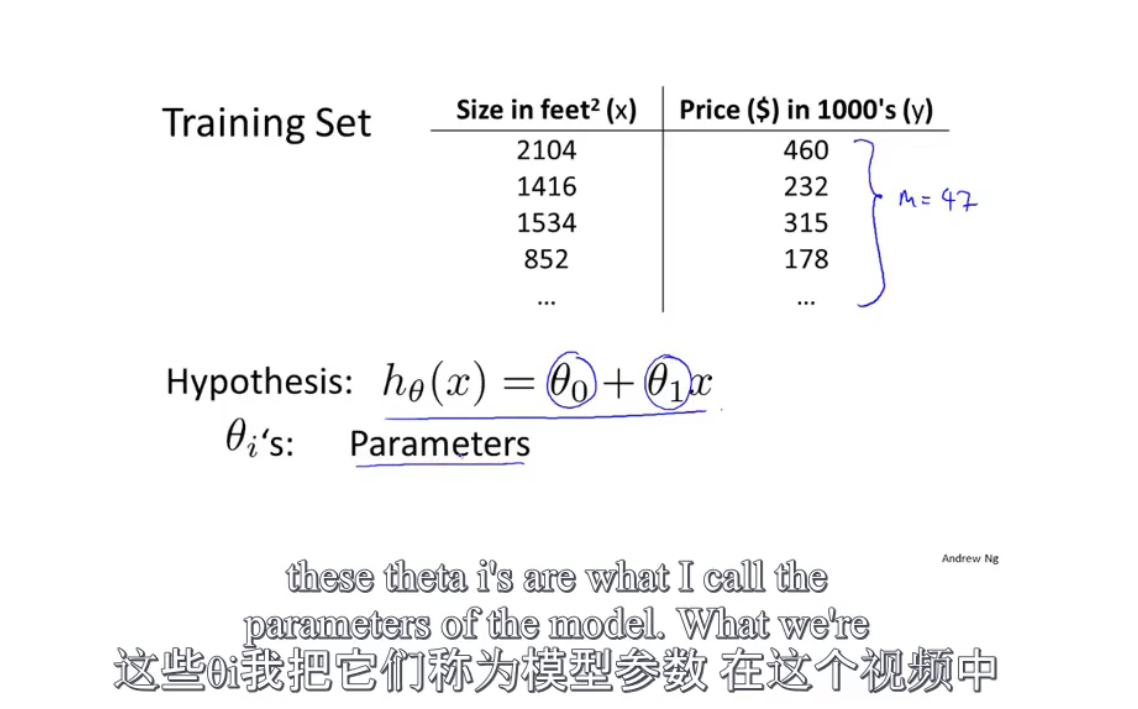
h为假设函数

J为代价函数
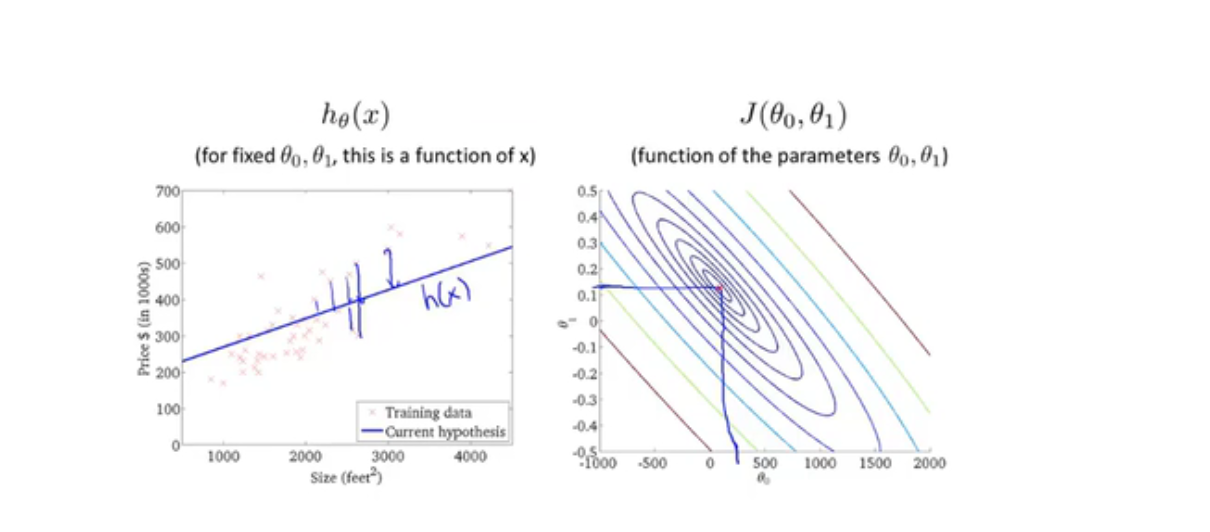
梯度下降算法


$\alpha$ 代表学习率(learning rate) 控制梯度下降的幅度
$\theta_0 \ and \ \theta_1$ 同时更新
depending on the initial condition, gradient descent may end up at different local optima.(根据初始条件,梯度下降可能会以不同的局部最优值结束。 )
线性回归算法(用直线模型拟合数据)

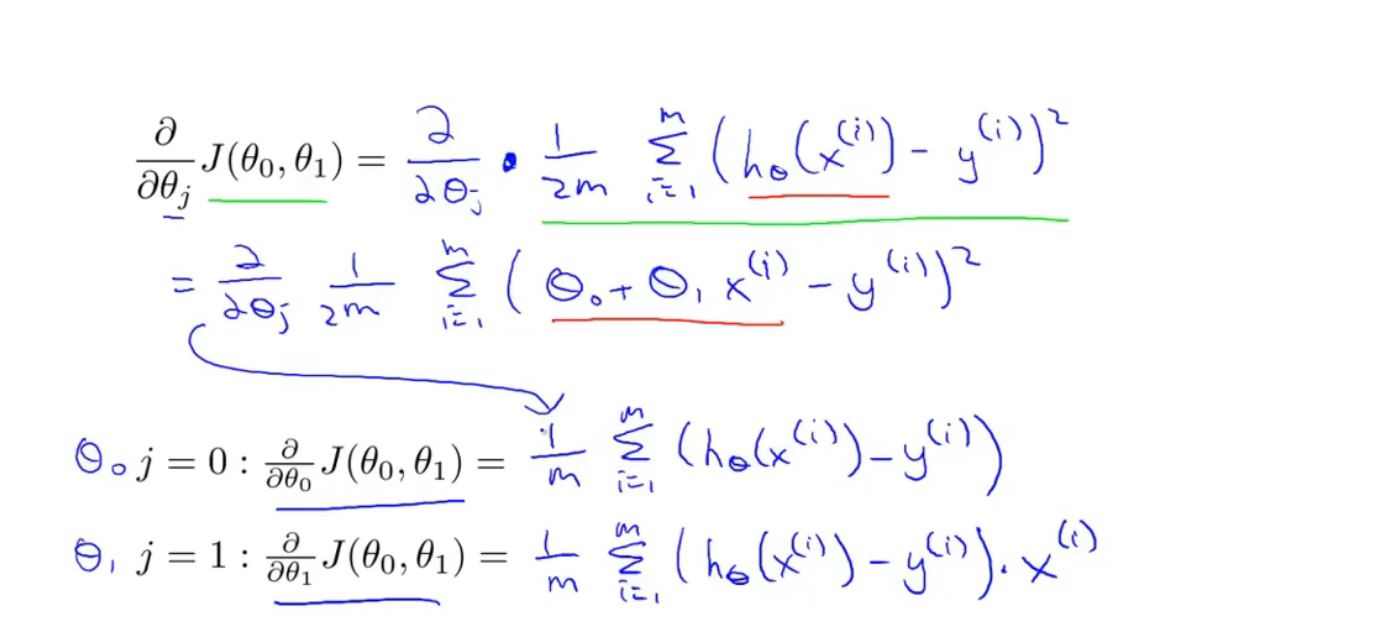

第三节
线代一些基础知识
第四节

多元梯度下降法


多元梯度下降法中的一些技巧
特征缩放
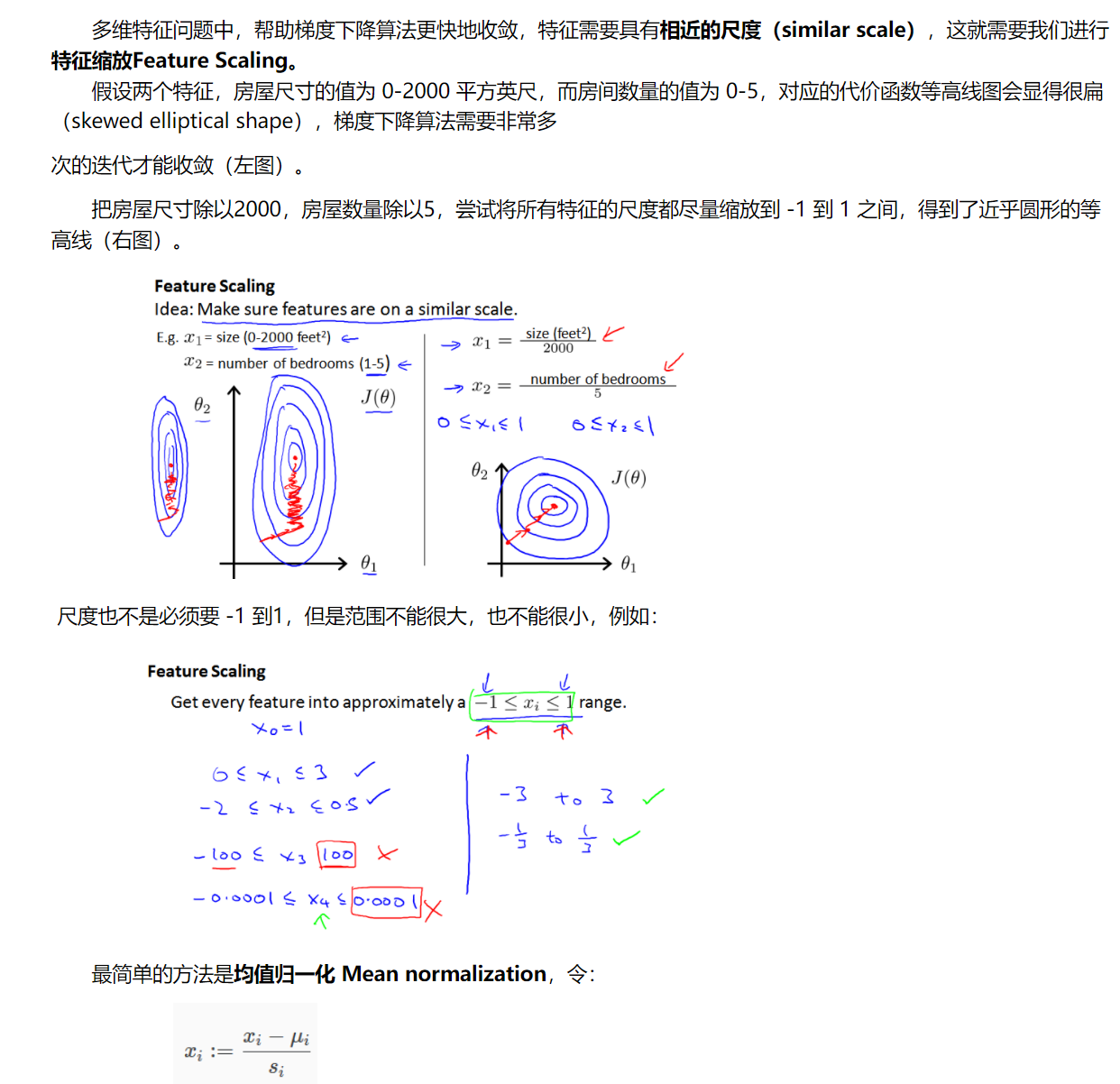

学习率


特征与多项式回归
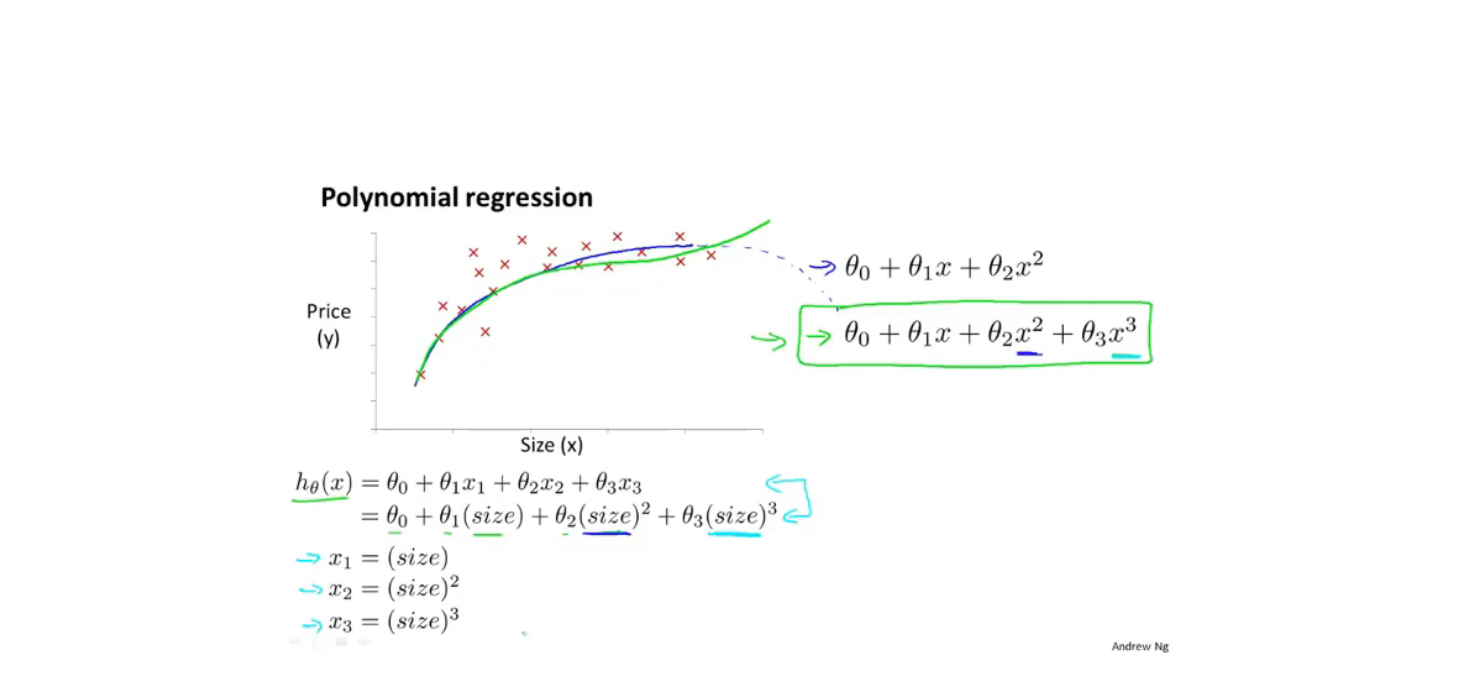
这时,特征缩放会显得特别重要
正规方程
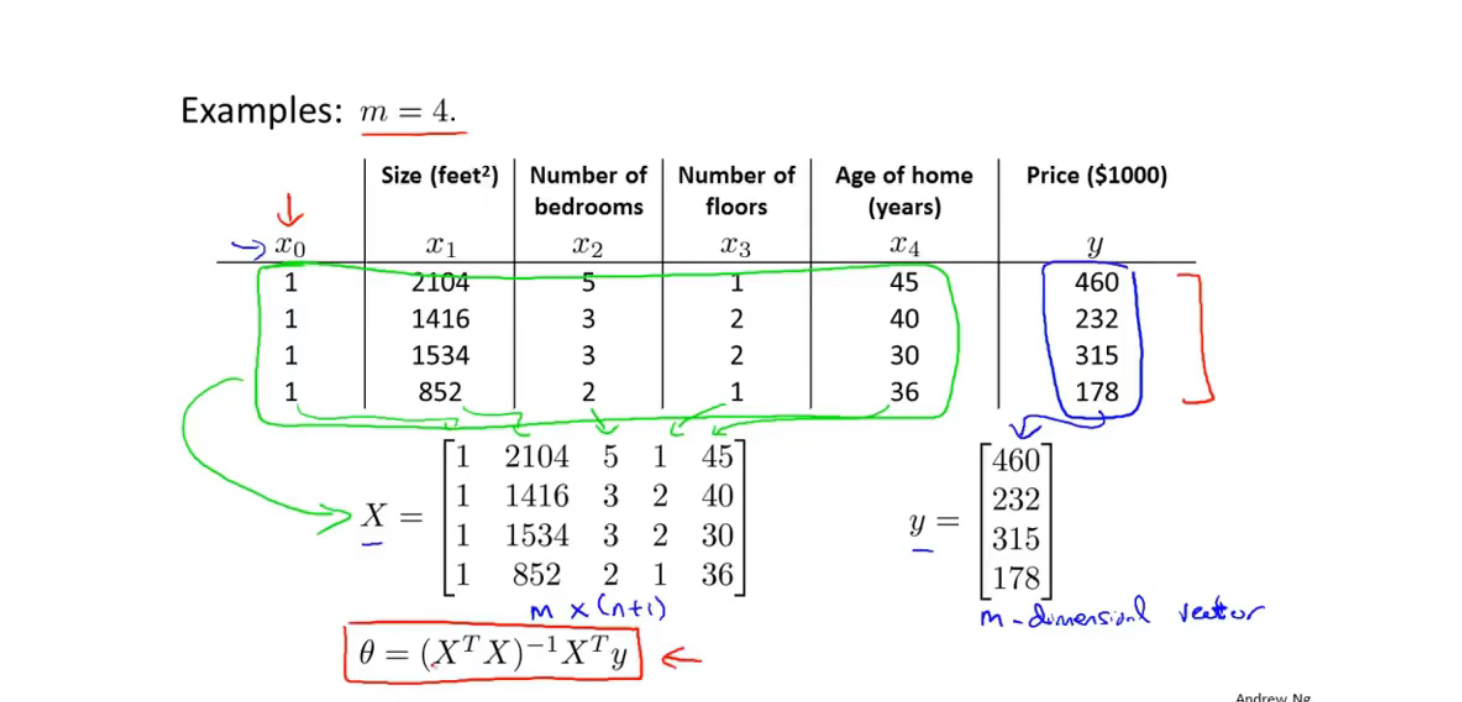


$X\cdot \theta=y$
$X^T\cdot X\cdot \theta=X^T\cdot y$
$\theta=(X^TX)^{-1}X^Ty$
第五节
代价函数
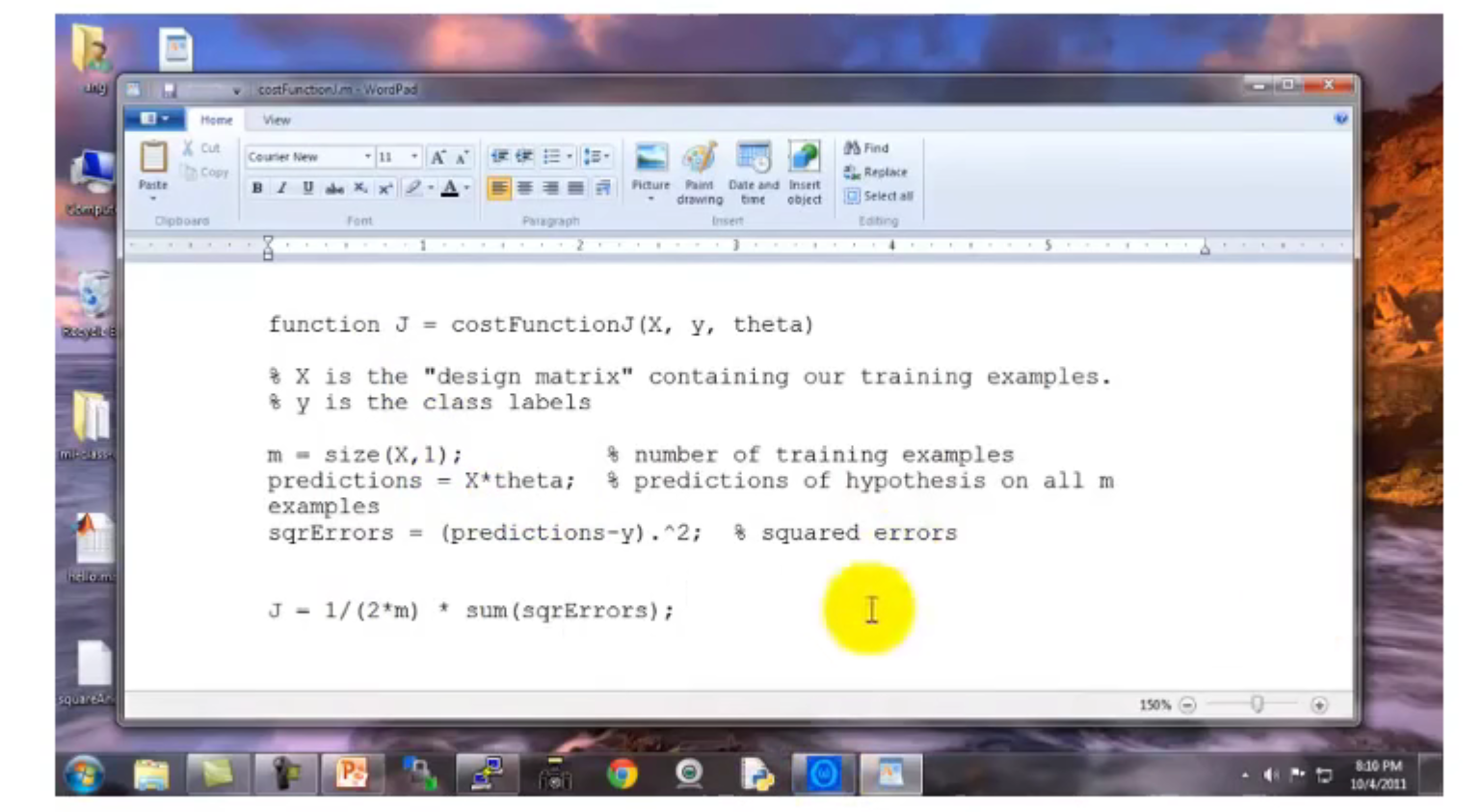
向量化优化


第六节
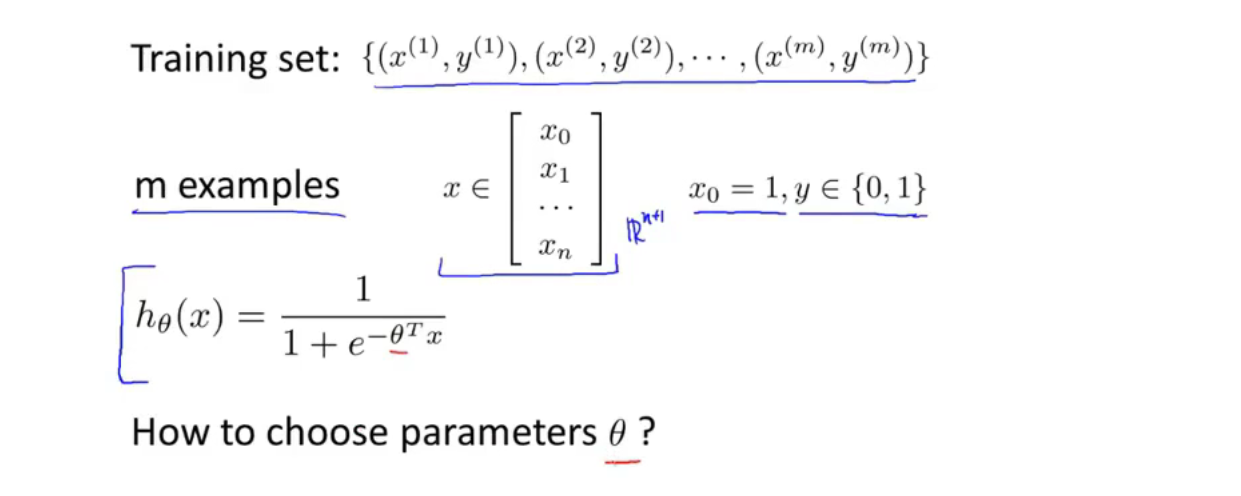
logistic 回归算法(分类算法)
Logistic 函数 $g(x)=\dfrac{1}{1+e^{-z}}$
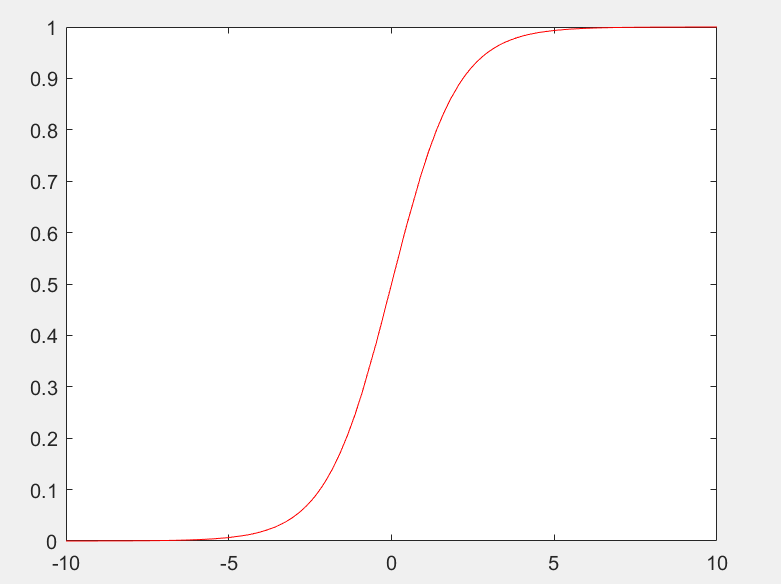
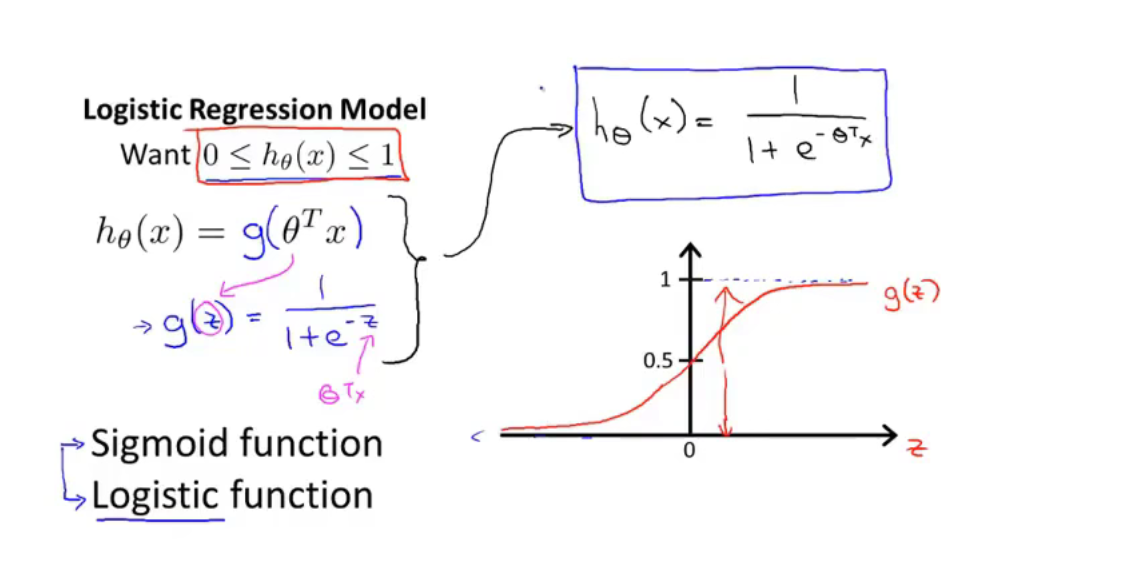

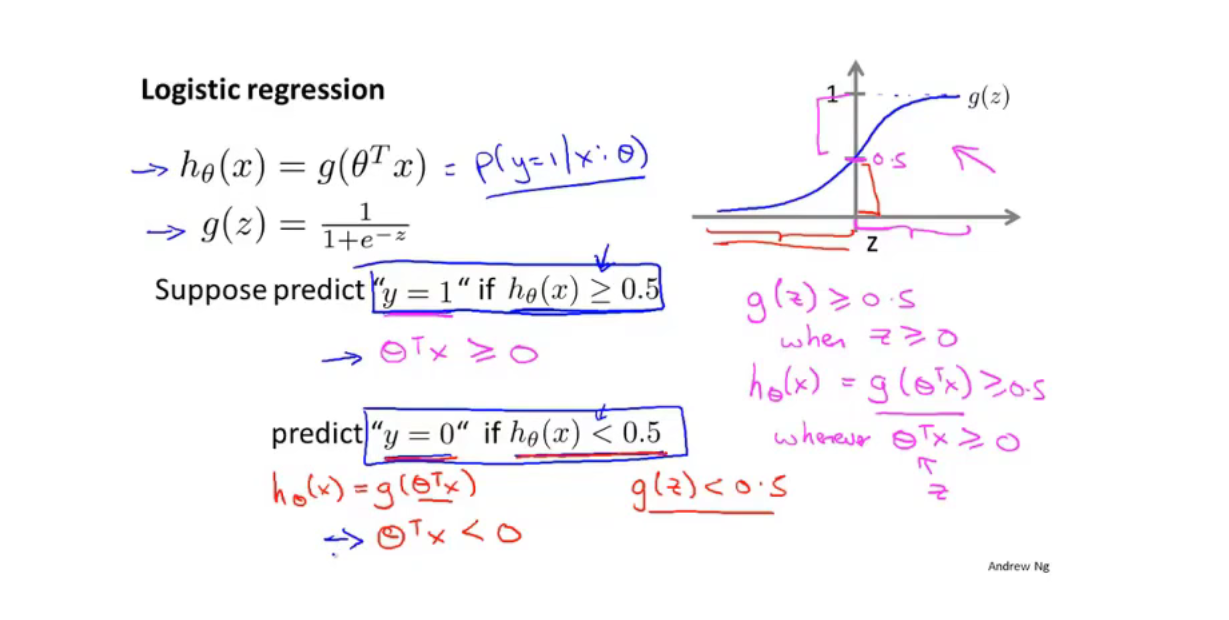
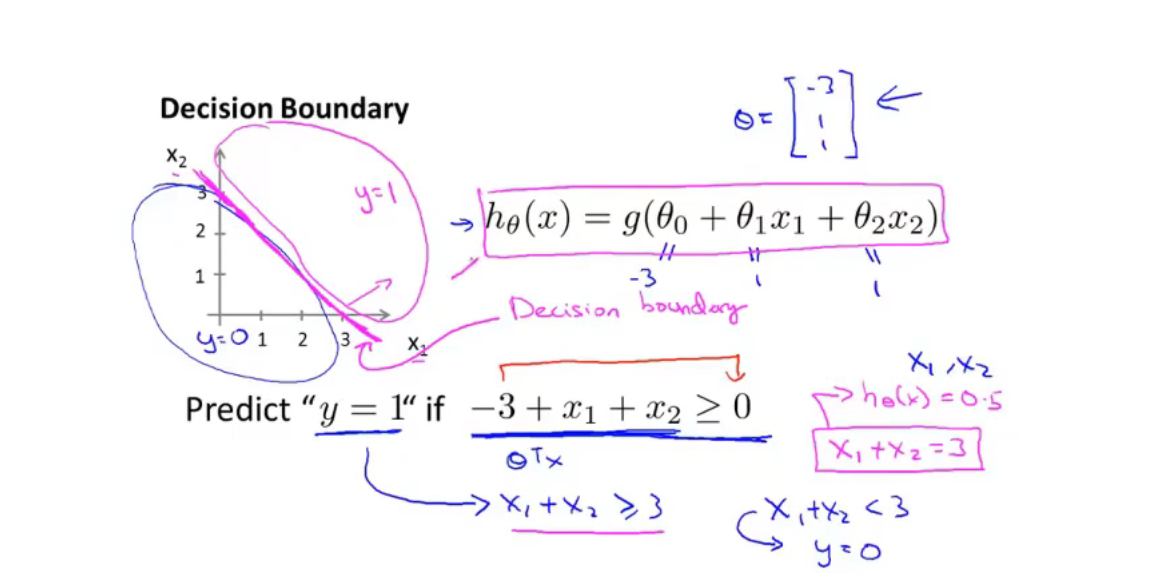
决策边界(decision boundary)是决策函数的属性,不是训练集的属性,我们使用训练集来拟合参数$\theta$
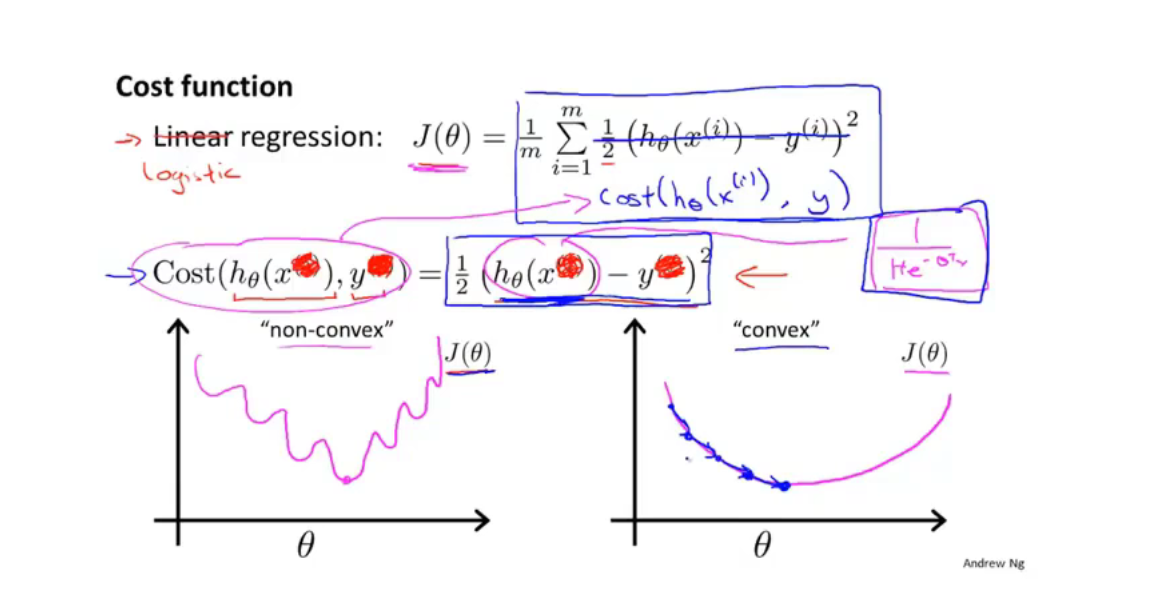
逻辑回归的代价函数无法使用梯度下降算法来收敛到全局最优(因为很容易使其收敛到局部最优)
因此需要将代价函数变形,使其可以使用梯度下降算法求解(使其变为凸函数,可以进行凸优化)

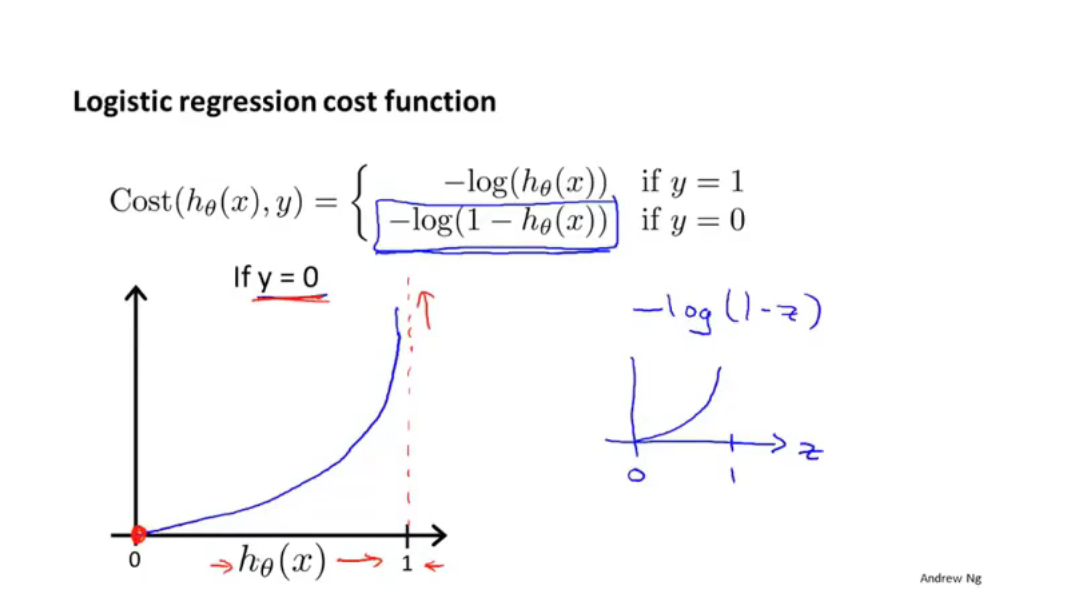
我们可以将分段函数写为一个函数



虽然最后逻辑回归中梯度下降求解的形式和线性规划中一致,但是$h_\theta$ 函数并不一样。不过特征缩放也可适用于逻辑回归

一些比梯度下降算法更高级的优化算法(收敛更快):

高级算法代码(可以看做加强版的梯度下降)

代价函数伪代码:
返回代价函数值和梯度值

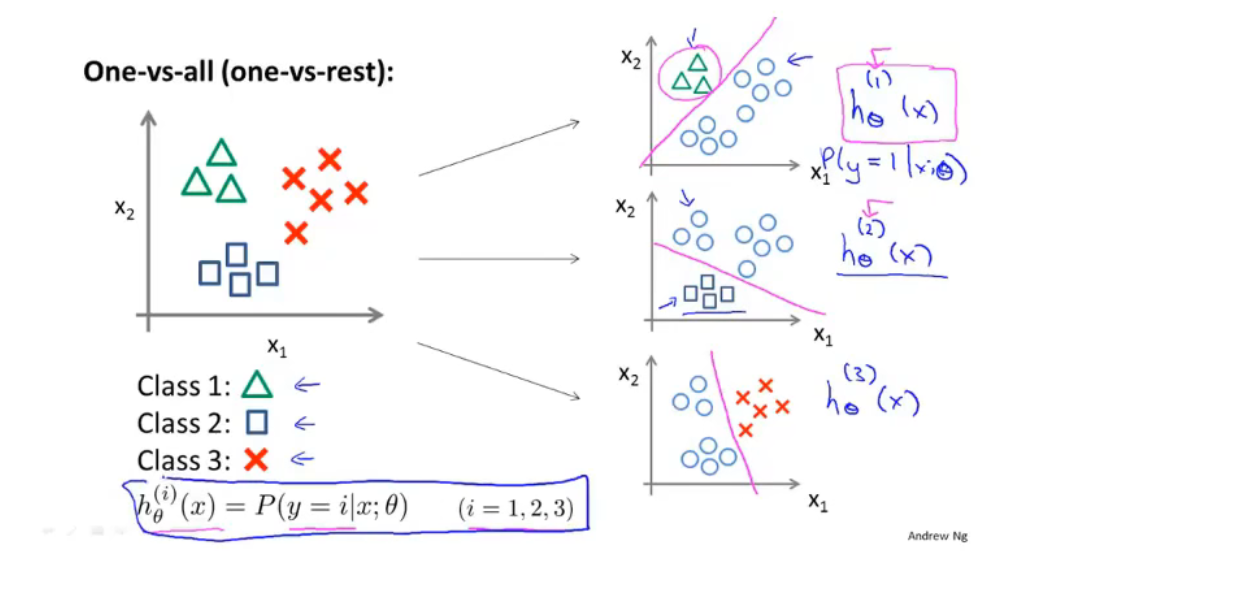
多类别分类问题 中一对多方法:
将多分类转化为若干个二分类问题,然后找概率y值最高的一个输出作为结果

第七节
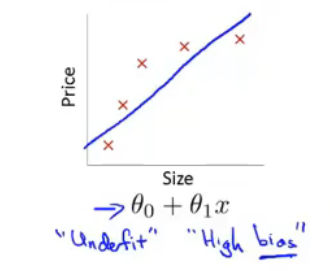
欠拟合(underfitting)high bias
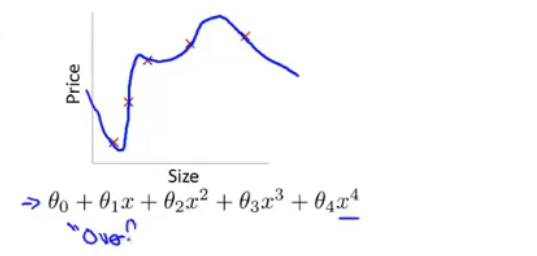
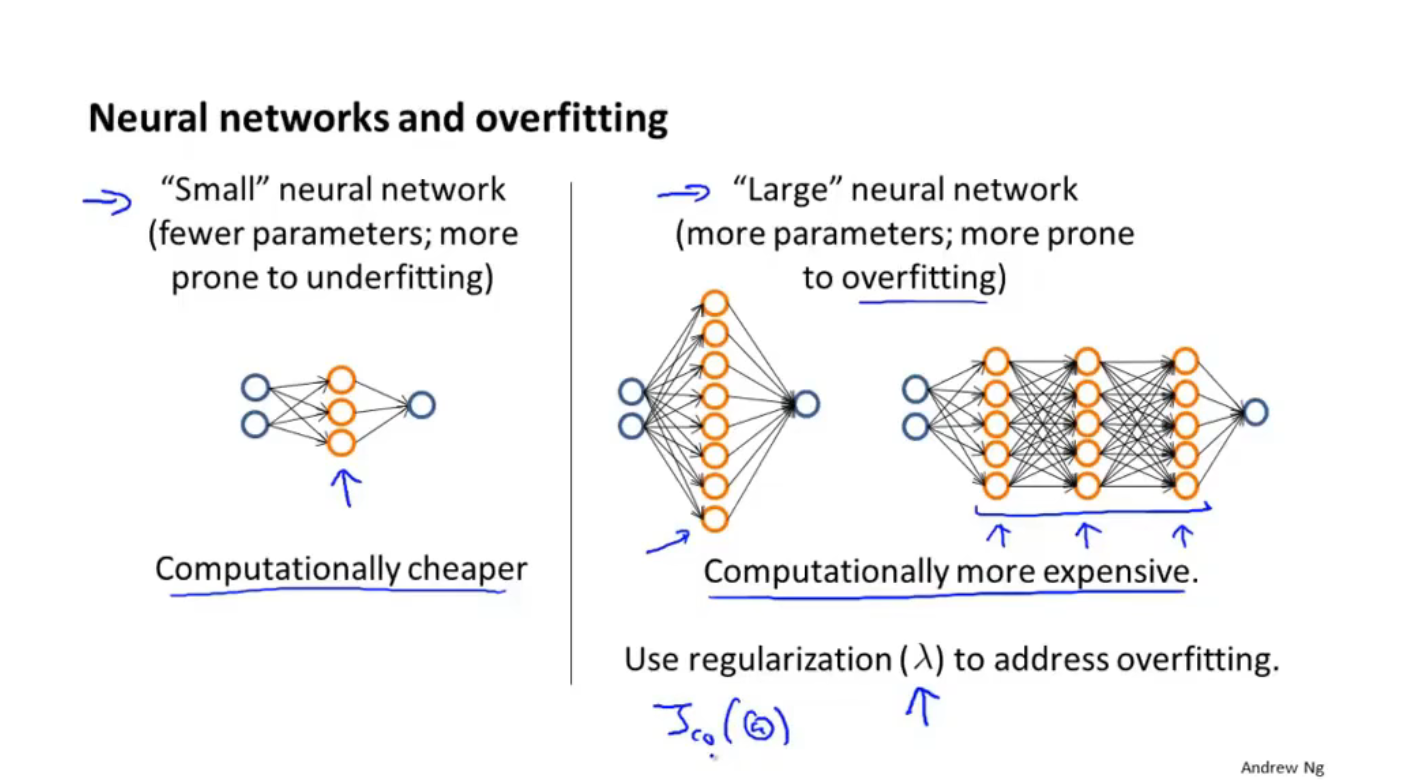
过度拟合问题(Overfitting):
过多变量并且较少数据时往往出现(高阶多项式)

解决方法:

正则化(Regularization):
加入惩罚,使参数尽量小,简化假设模型(不减少特征)

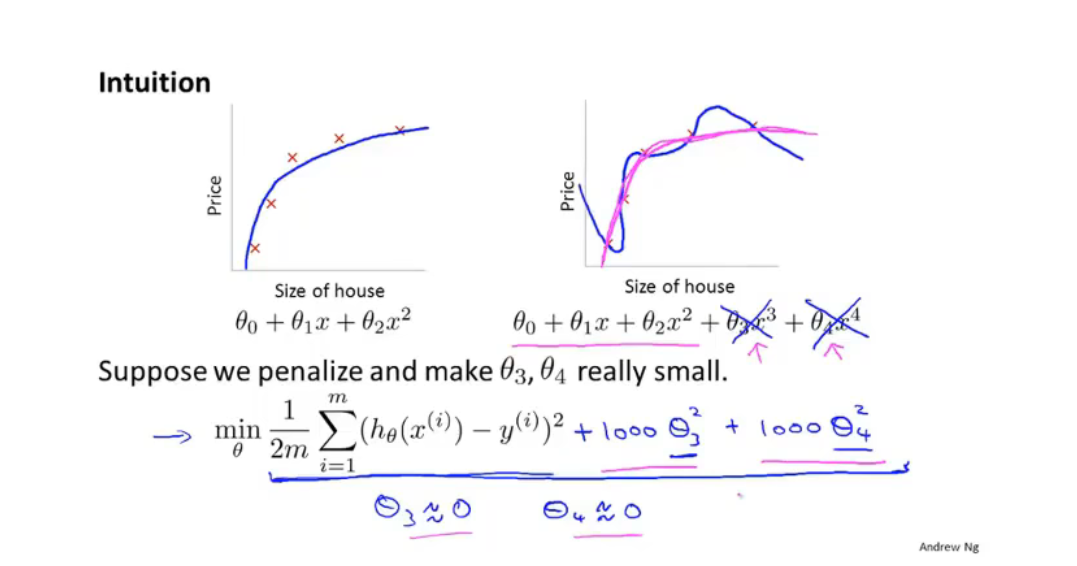
例如房屋预测模型,加入正则项,目的是使得$\theta$尽可能的小
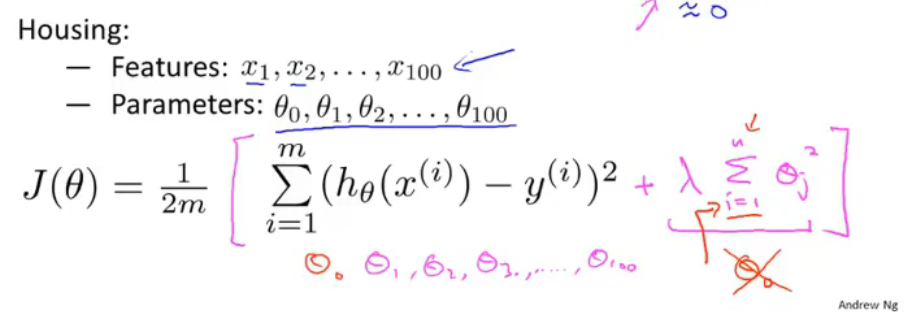
正则化参数$\lambda$ 作用有两个,一个是作为正则项拟合数据,另一个引入惩罚是为了使$\theta$ 尽可能的小,避免过拟合。
但是如果$\lambda$ 值太大,那么引入的惩罚过大,导致所有$\theta$都接近为0,会出现欠拟合

线性回归的正则化
梯度下降
引入$\lambda$进行梯度下降,$1-\alpha\dfrac{\lambda}{m}$ $< 1$ ,(m是一个比较大的数),所以$\theta$会不断缩小
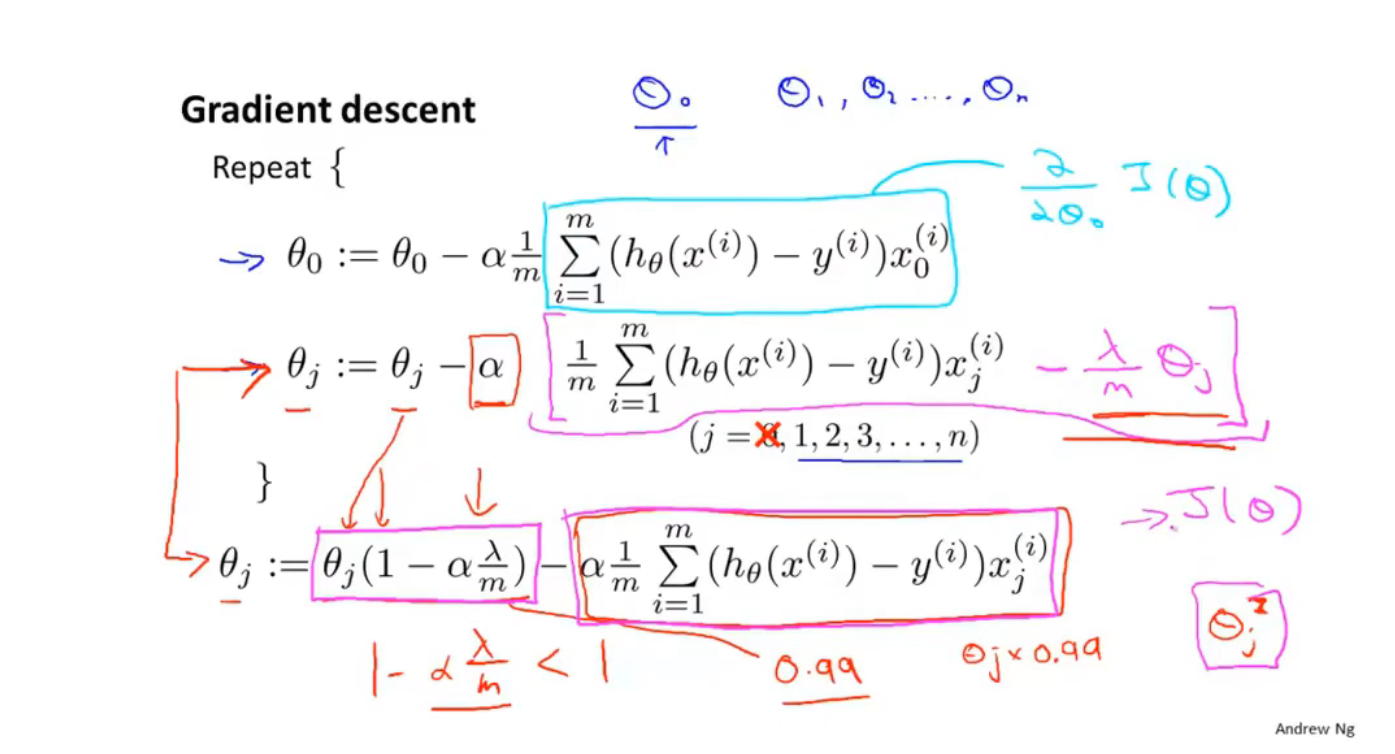
正规化


Logistic 回归正则化(逻辑回归):
公式形式与线性回归一致,但是逻辑回归引入了逻辑函数


第八节 神经网络
非线性假设
神经网络:

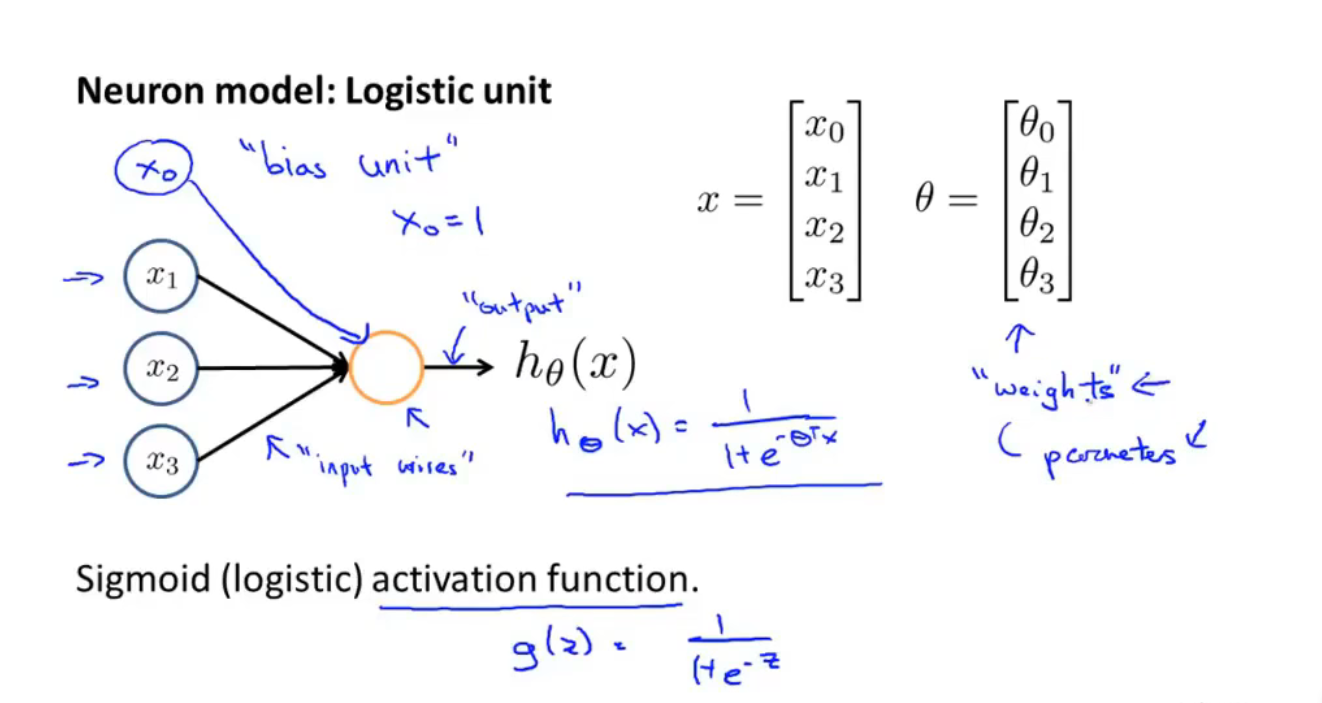
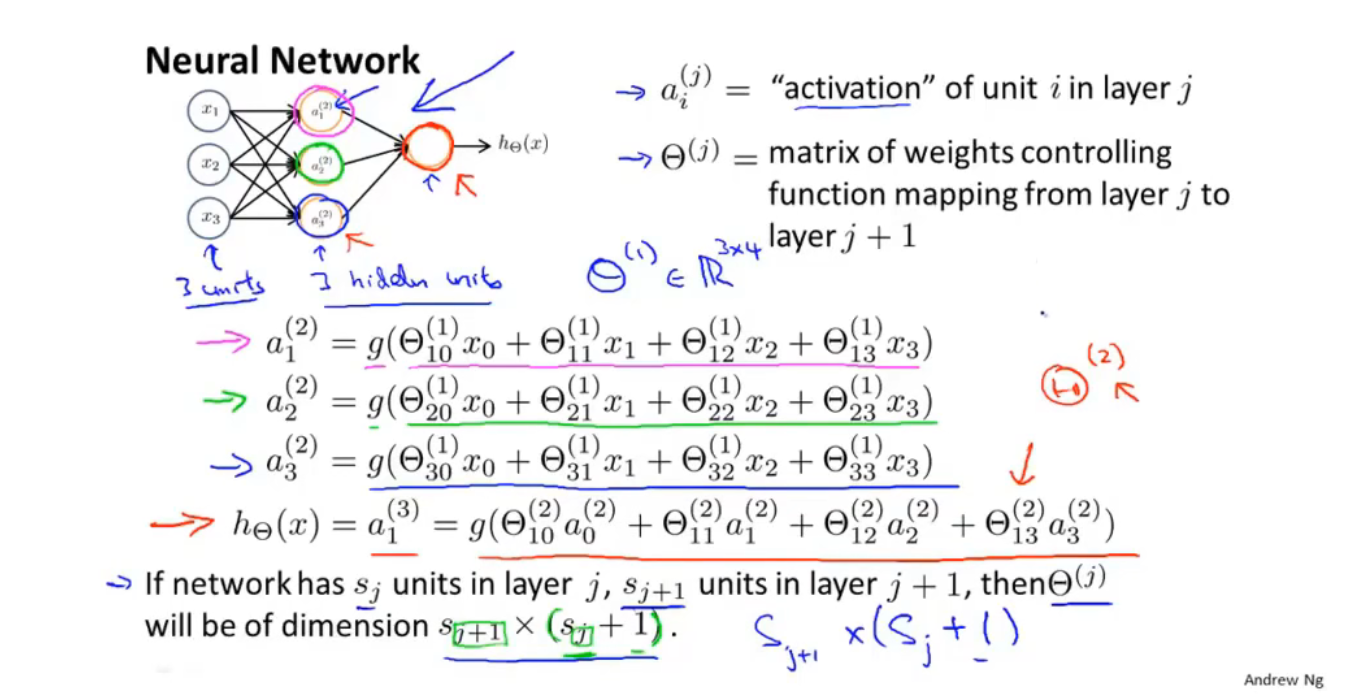
前向传播(向量化计算h(x))
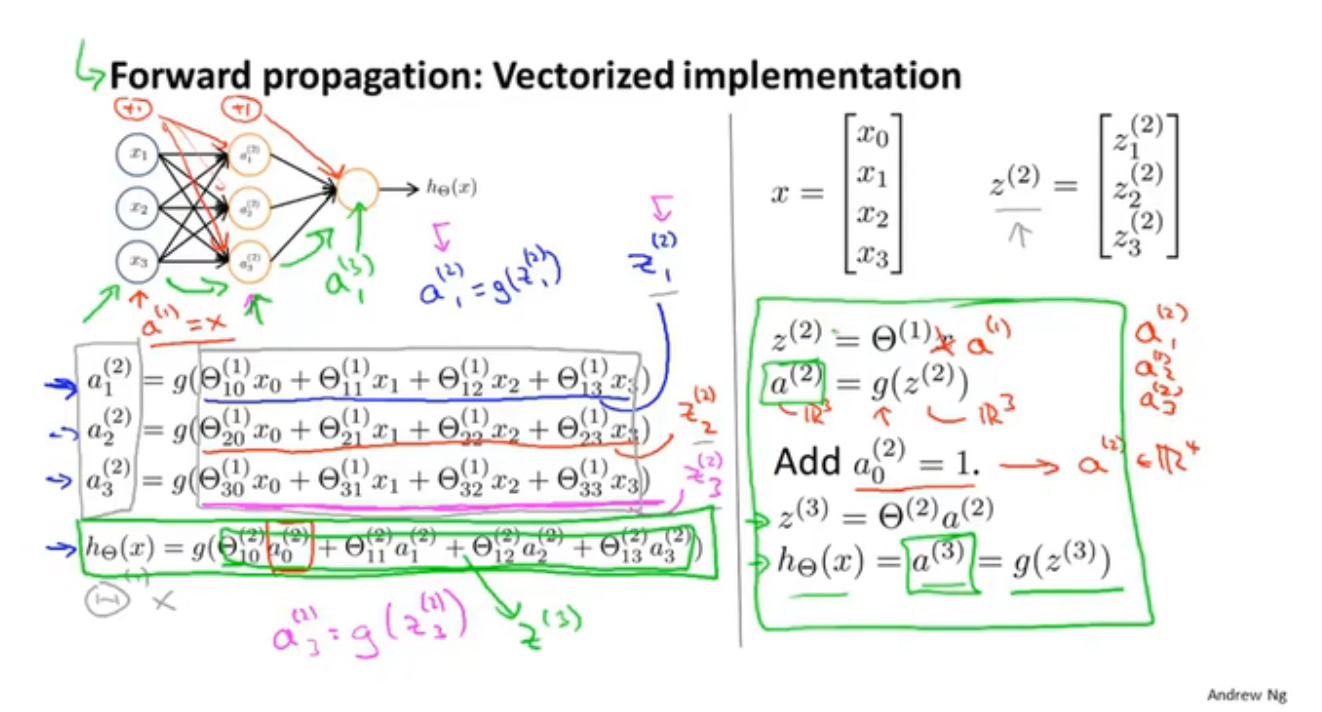
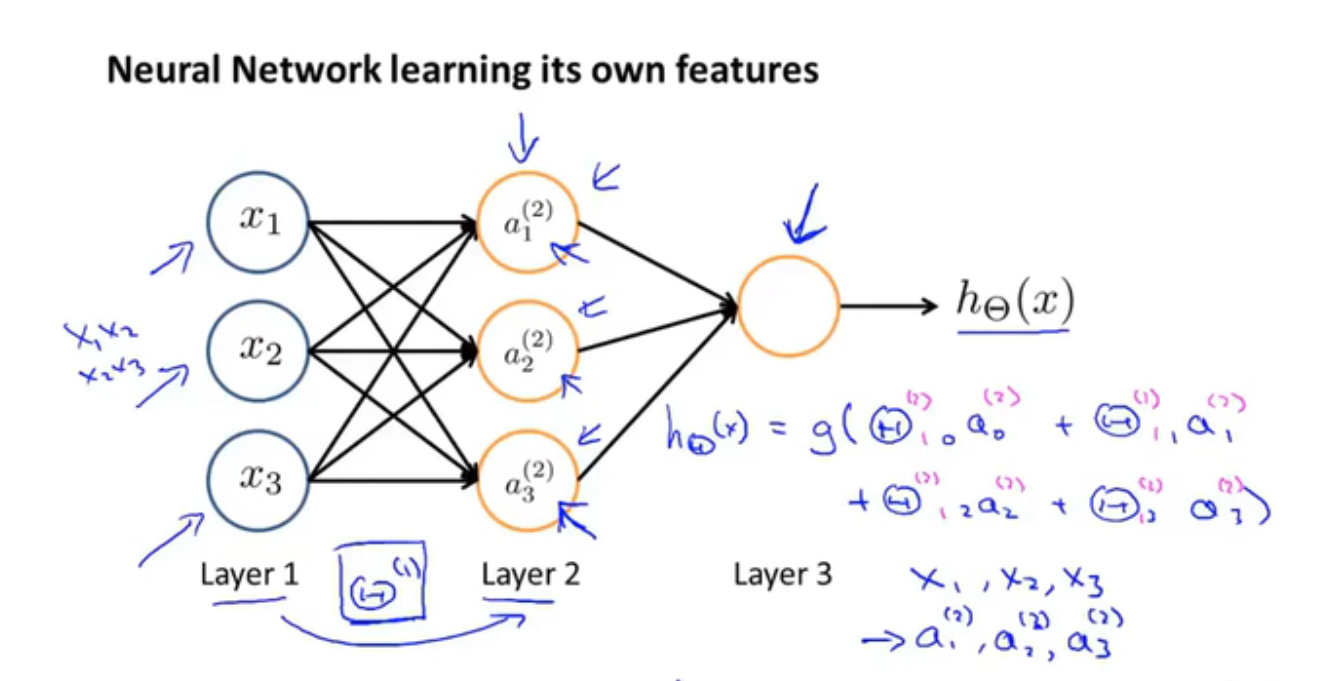
神经网络训练自己的特征
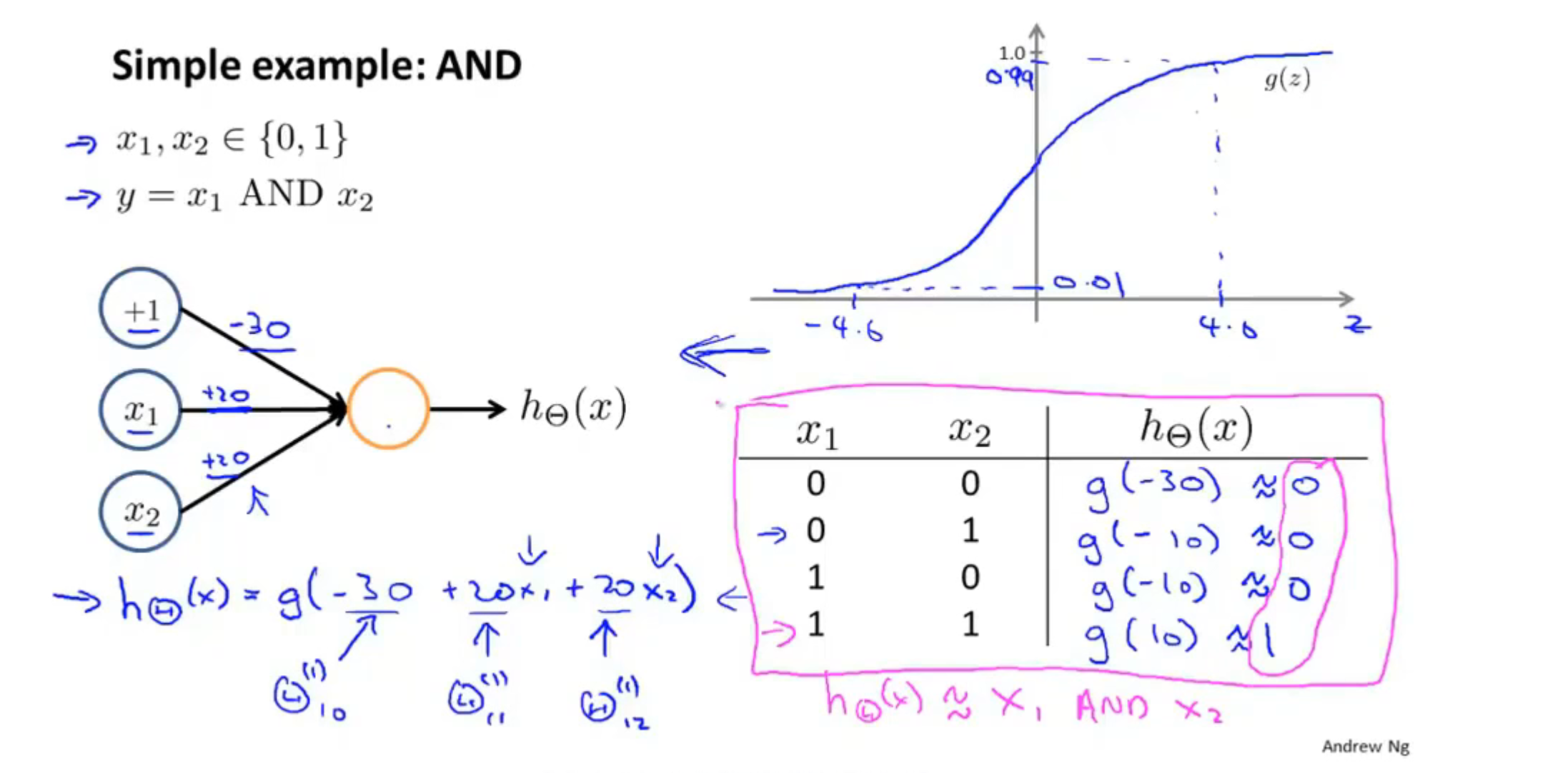
逻辑与
或运算

非运算
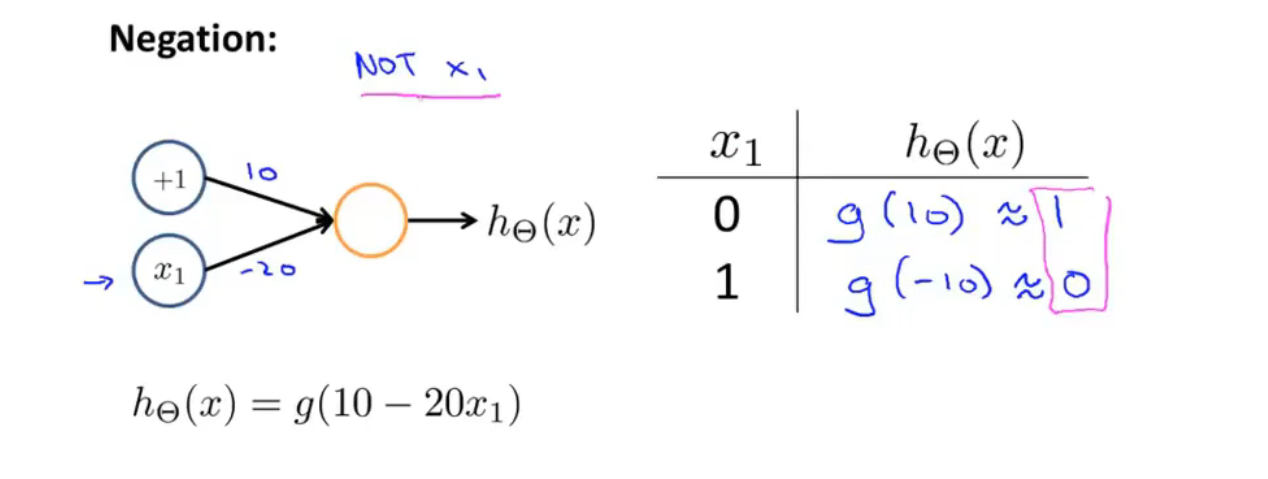
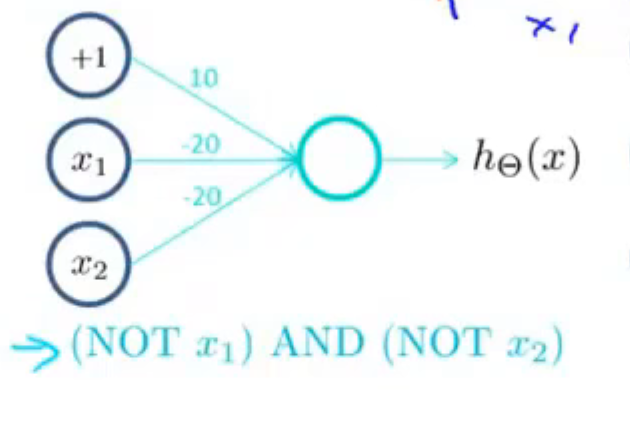
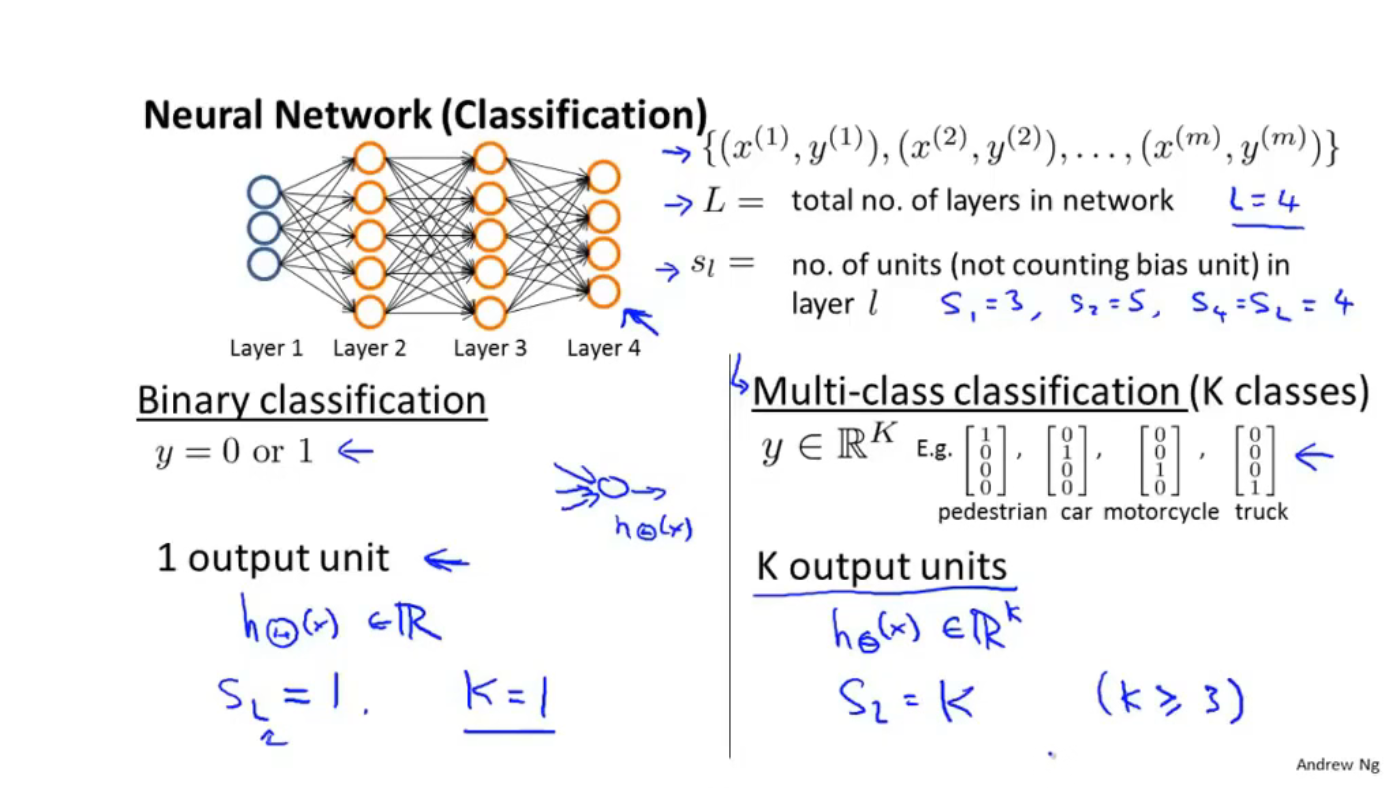
第九节
代价函数
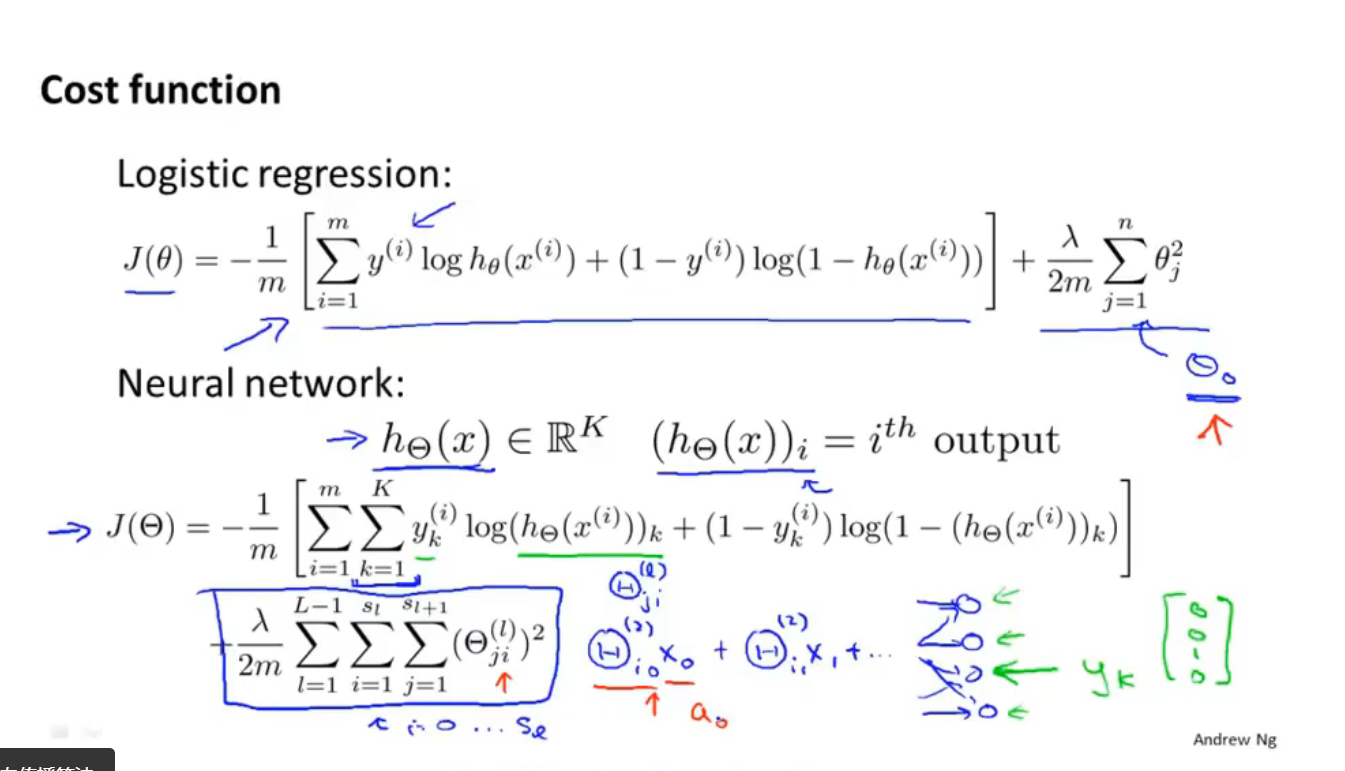
反向传播算法
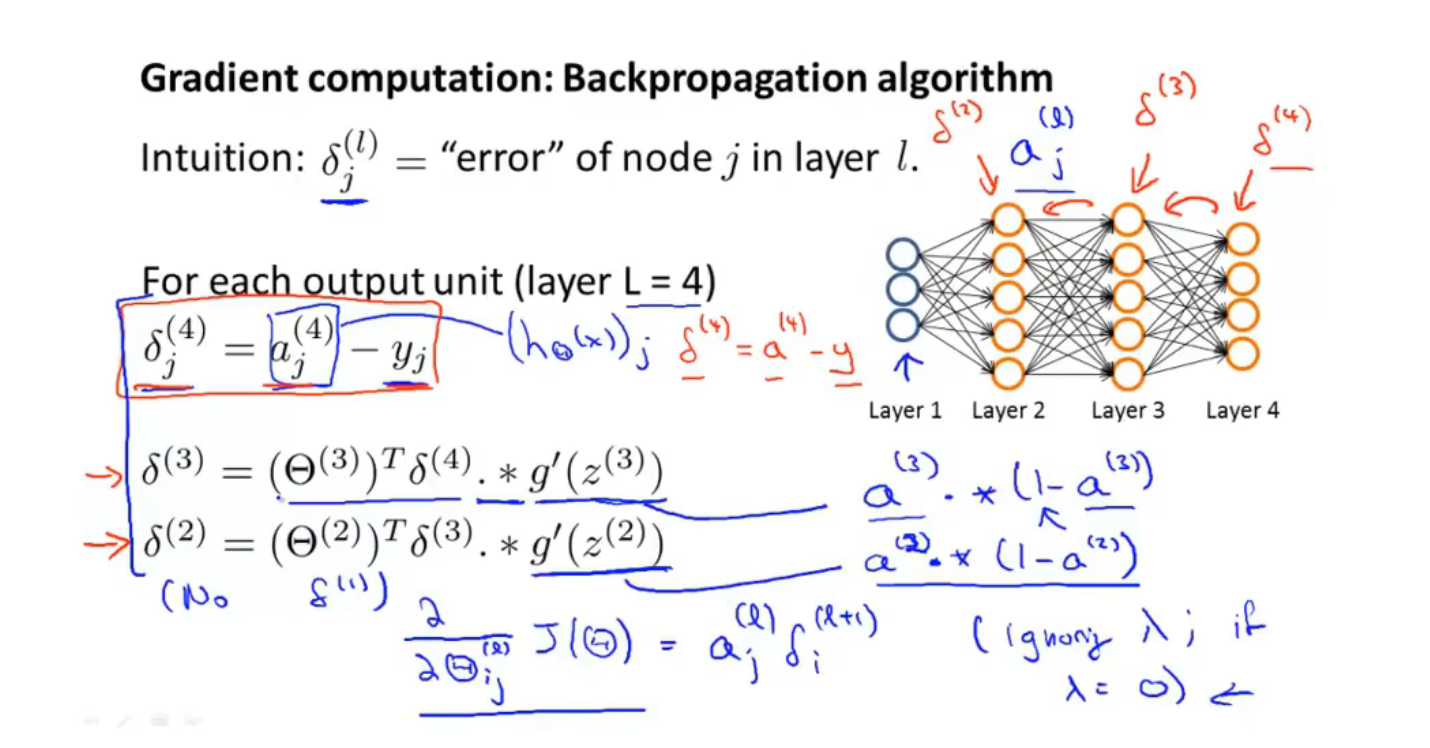

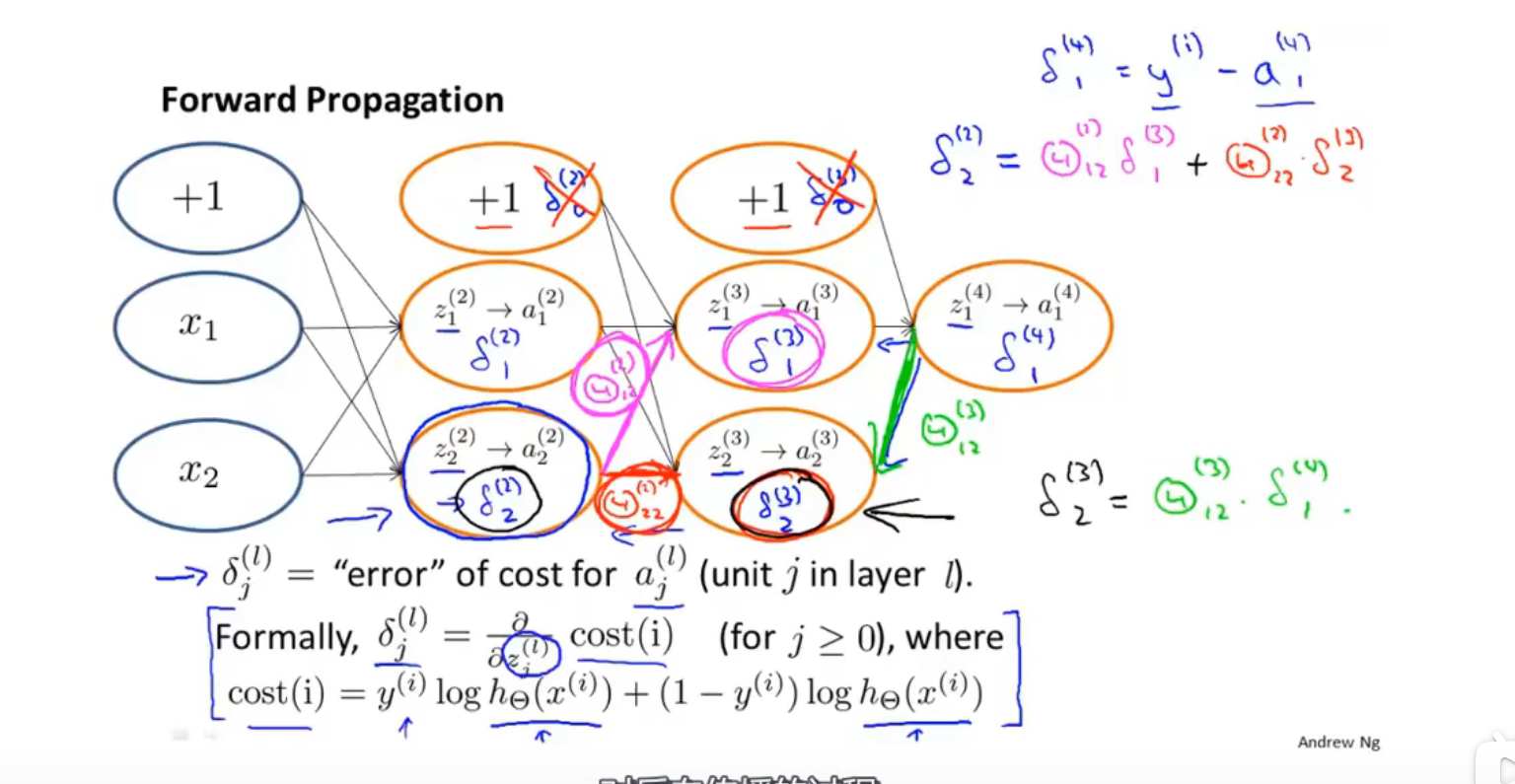


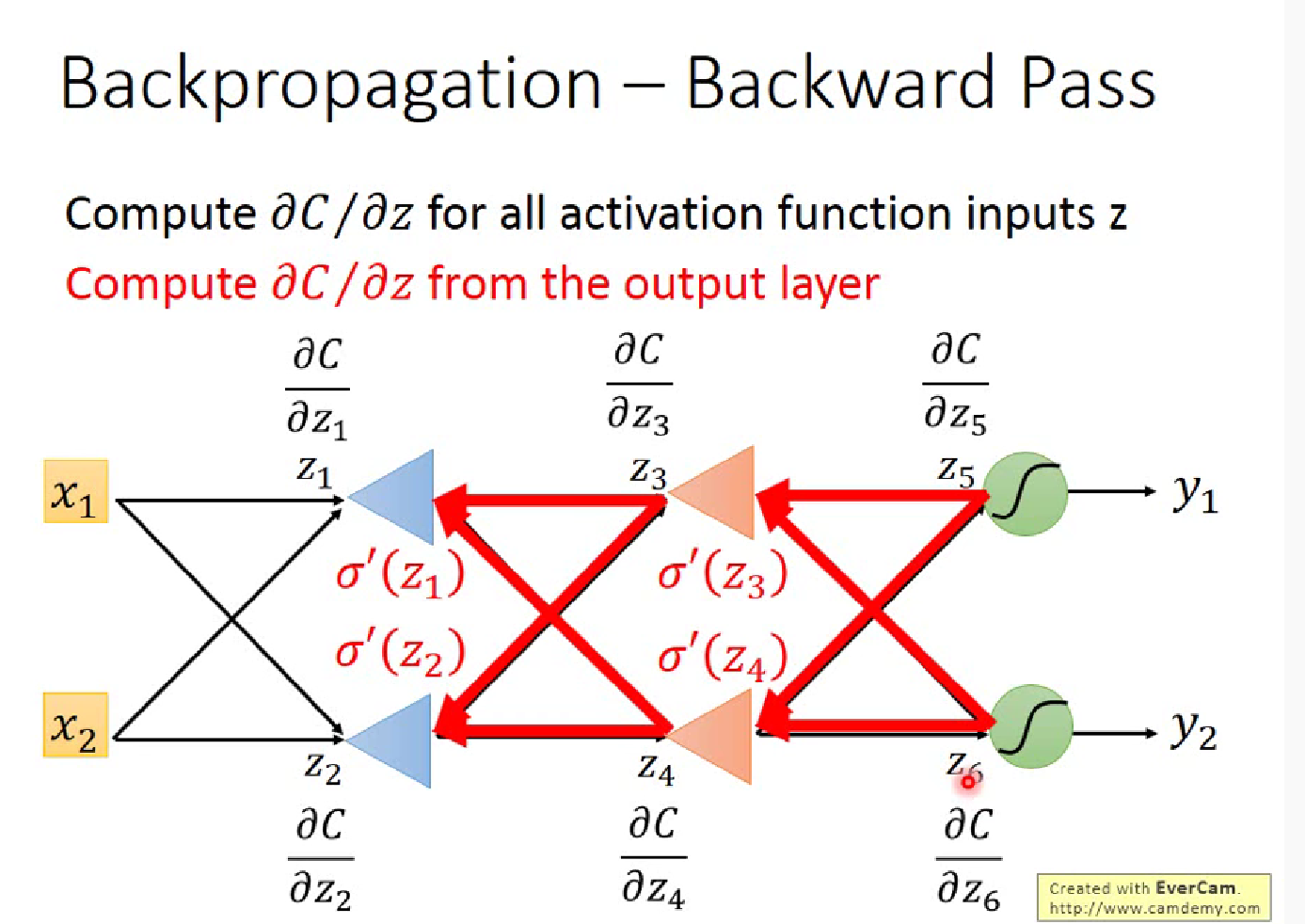
李宏毅解释的反向传播
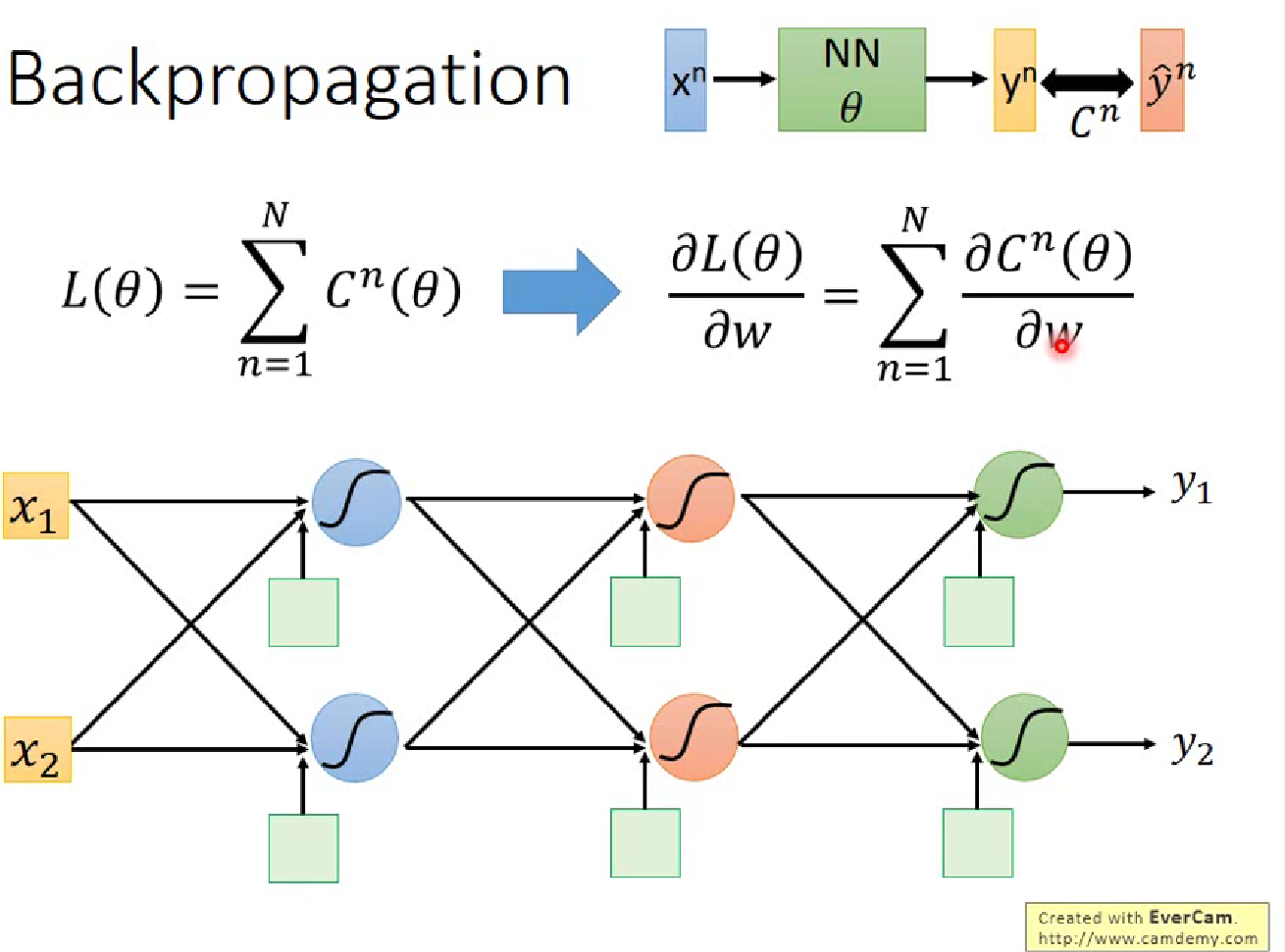
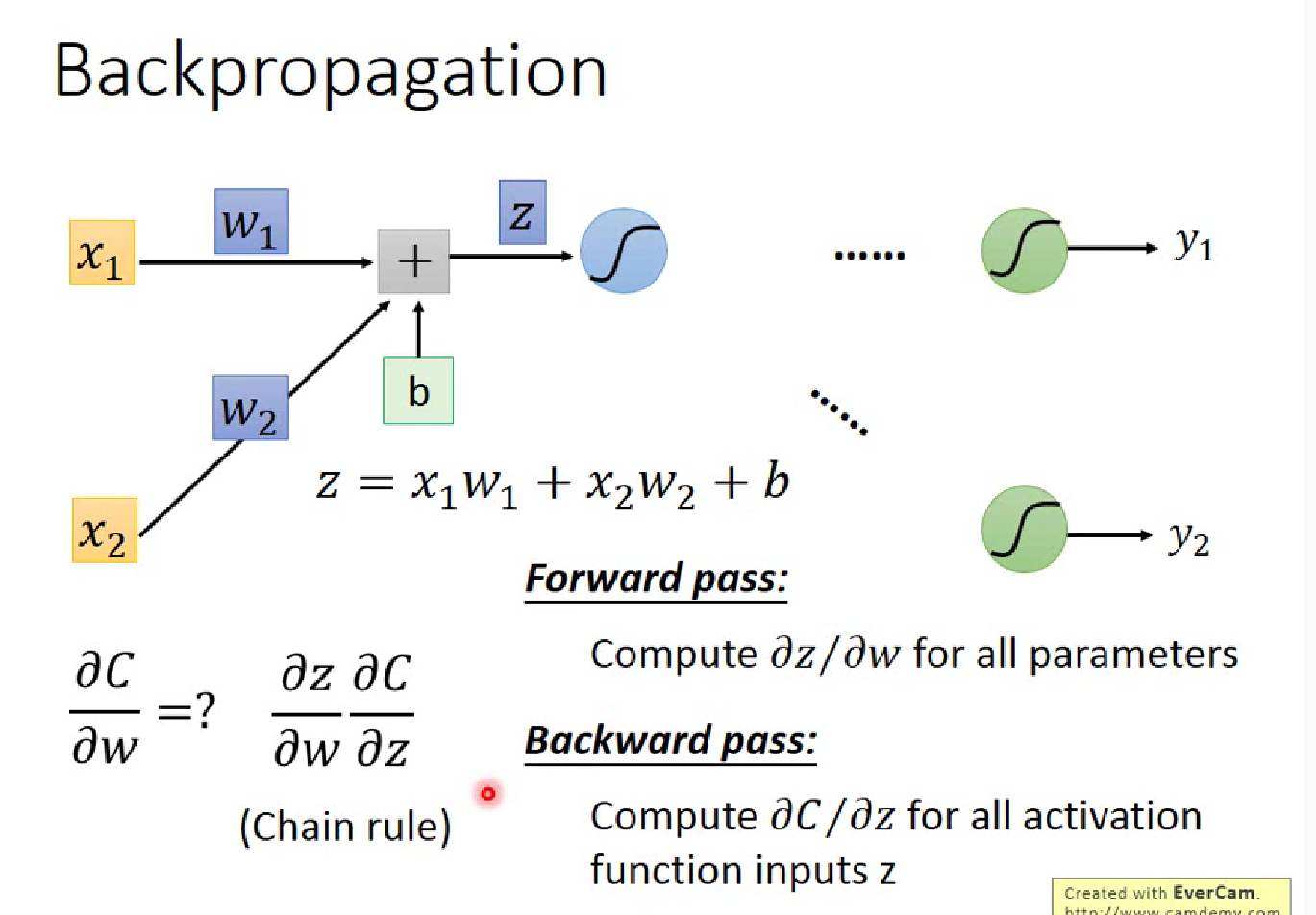
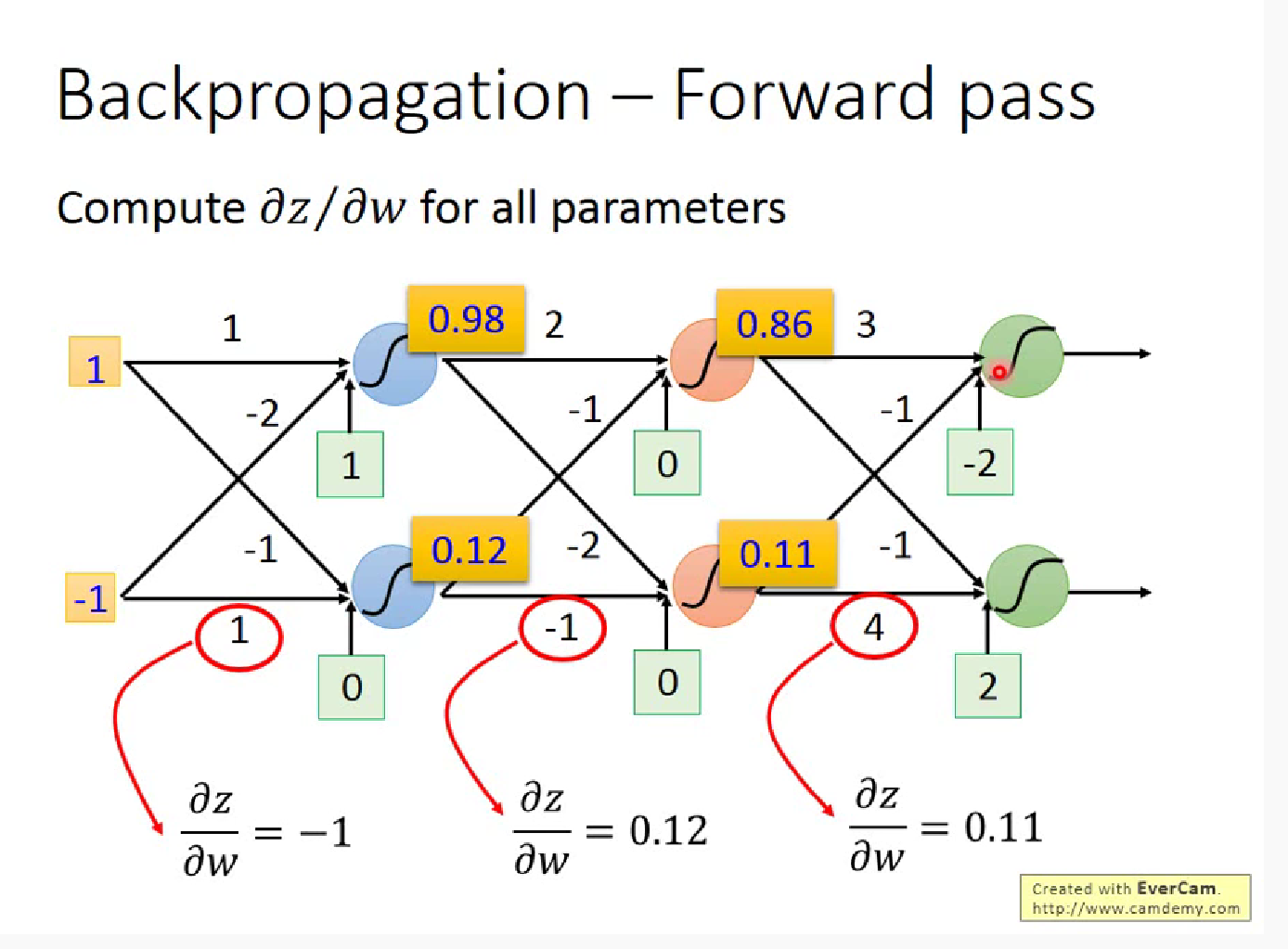
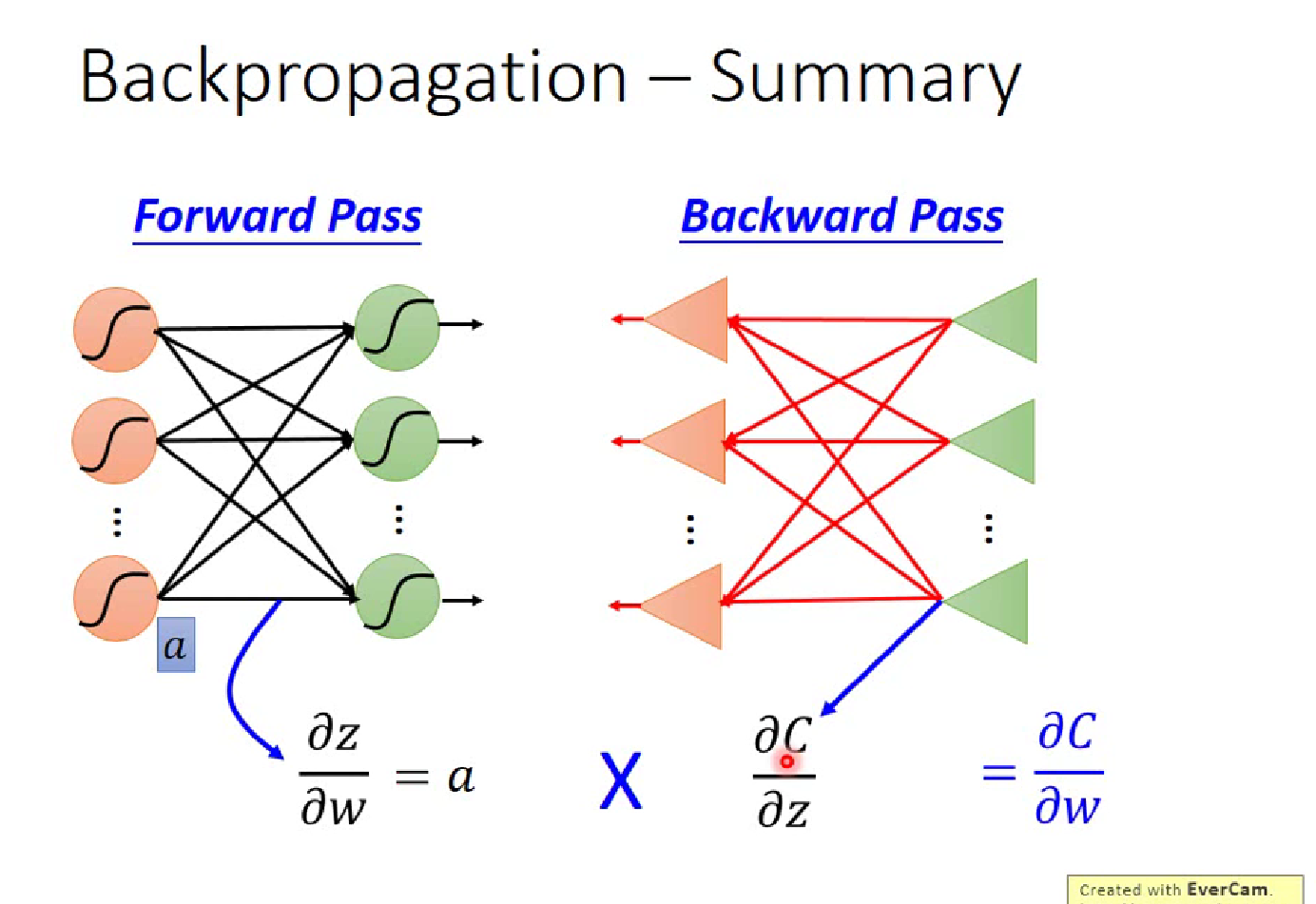
显然对于$\partial z /\partial w$(z=x1$\cdot$w1+x2$\cdot$w2+b ) ,$w_i$的偏微分就是前面的”输入” $x_i$,这就是一个Forward pass 的过程
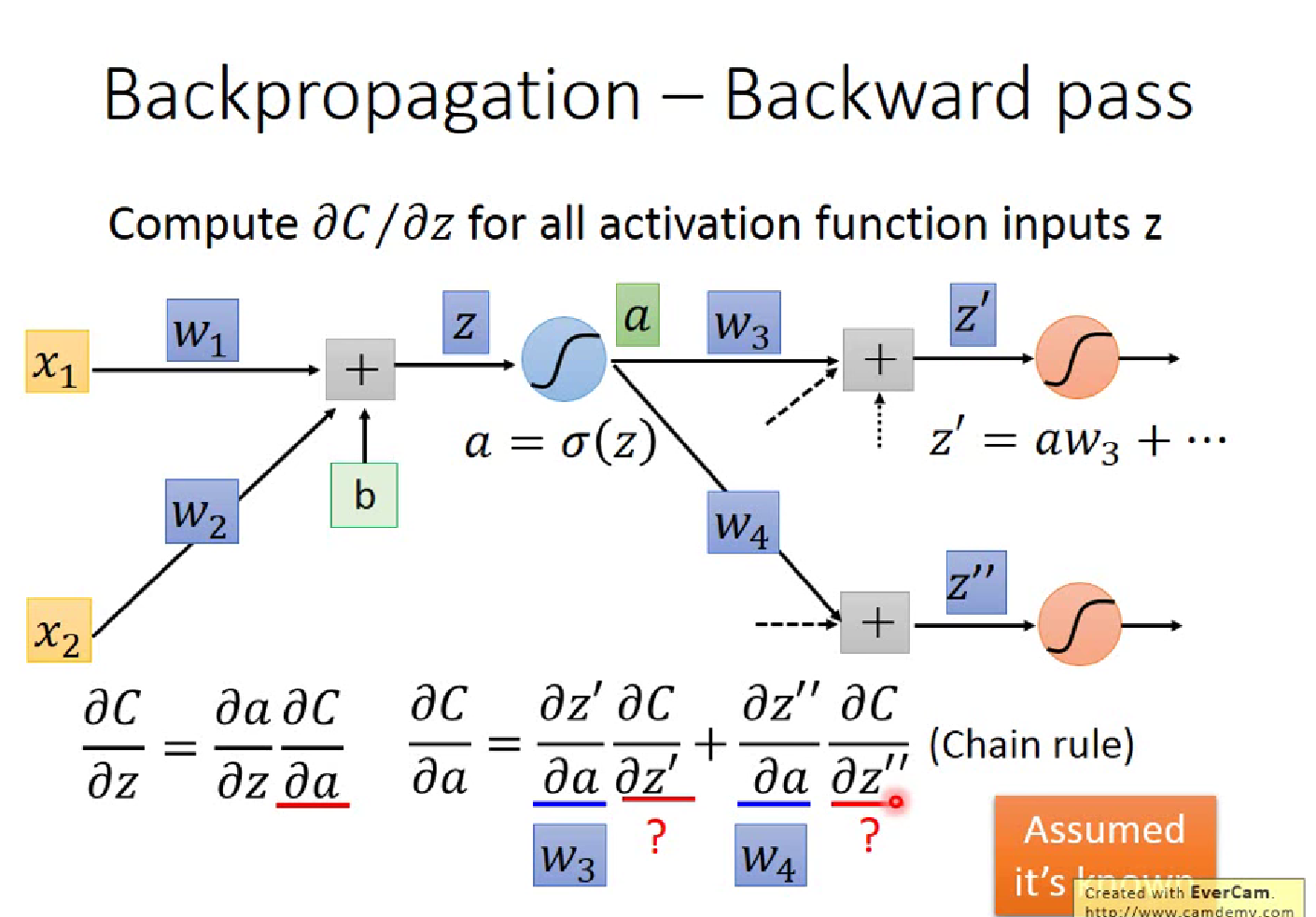
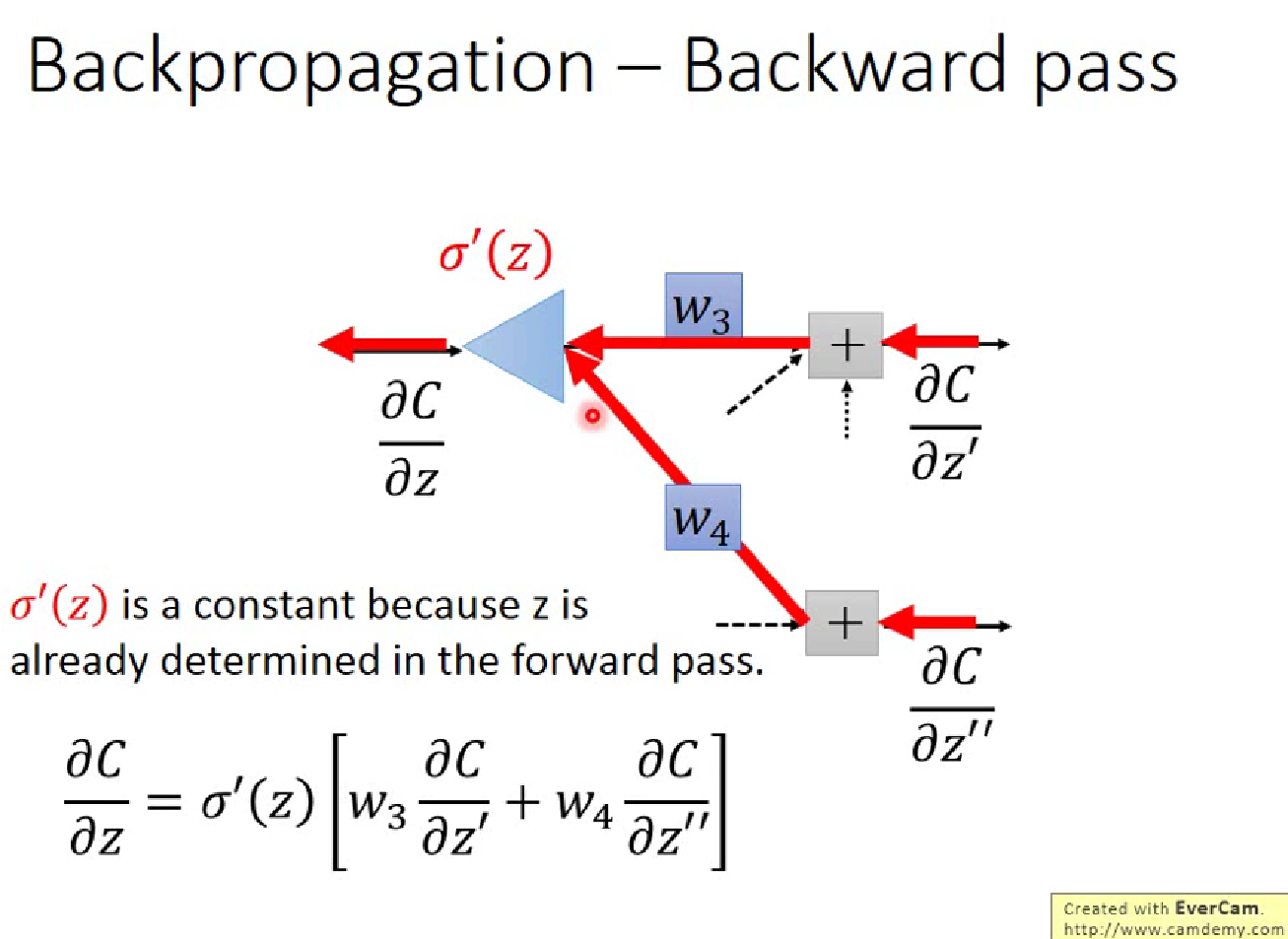
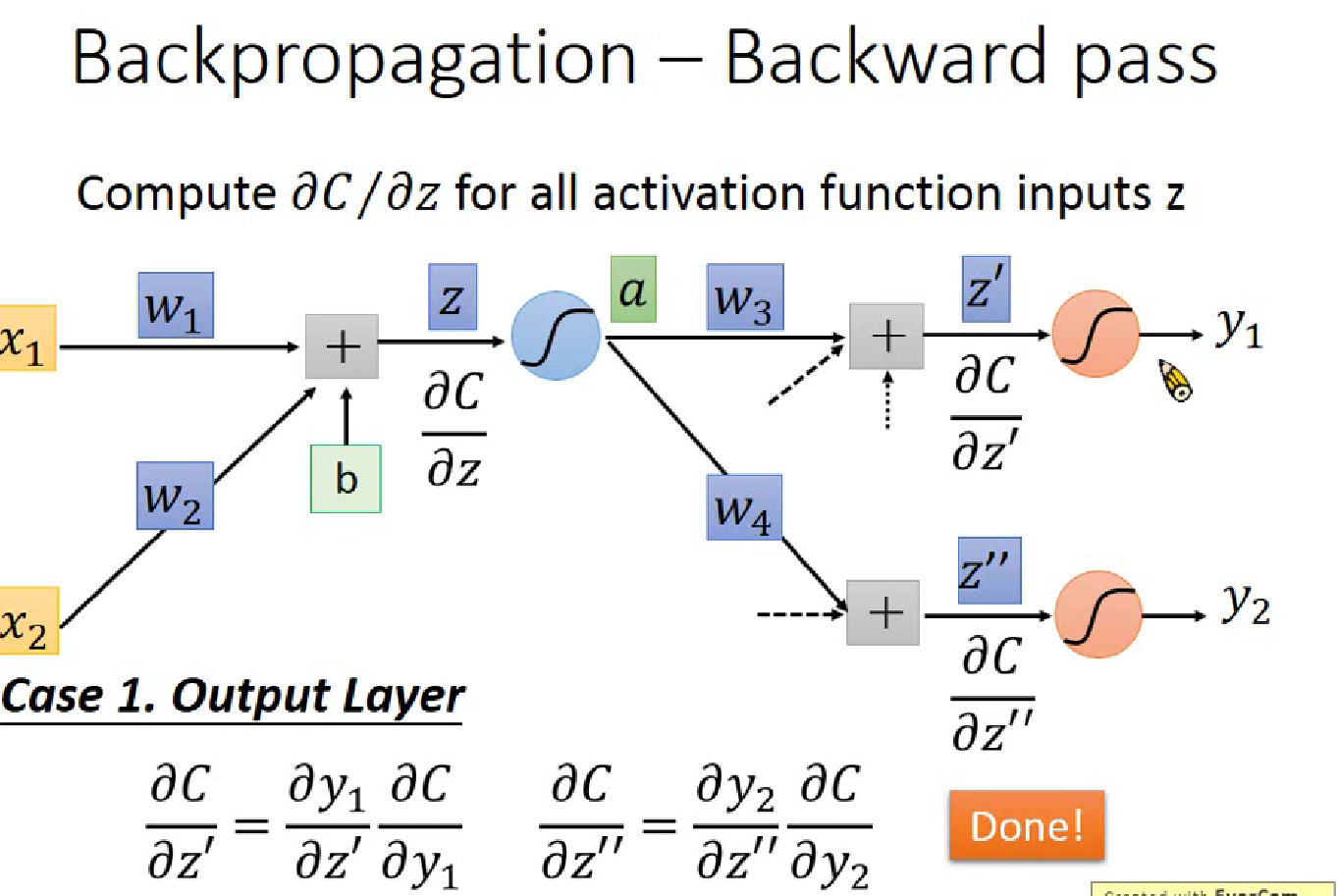
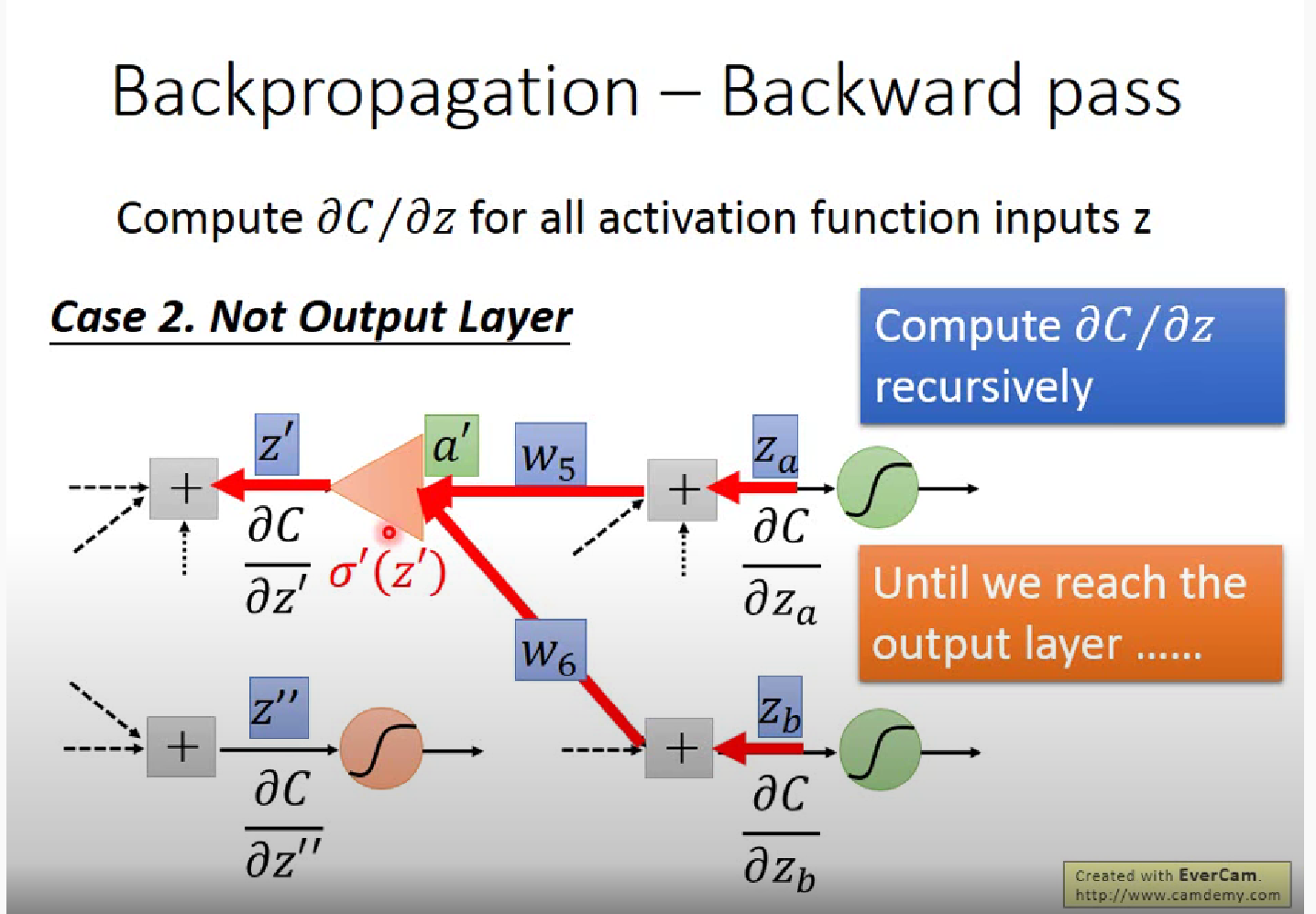
Backward Pass,就类似于反向建立Neural Network,计算$\partial C/\partial z$
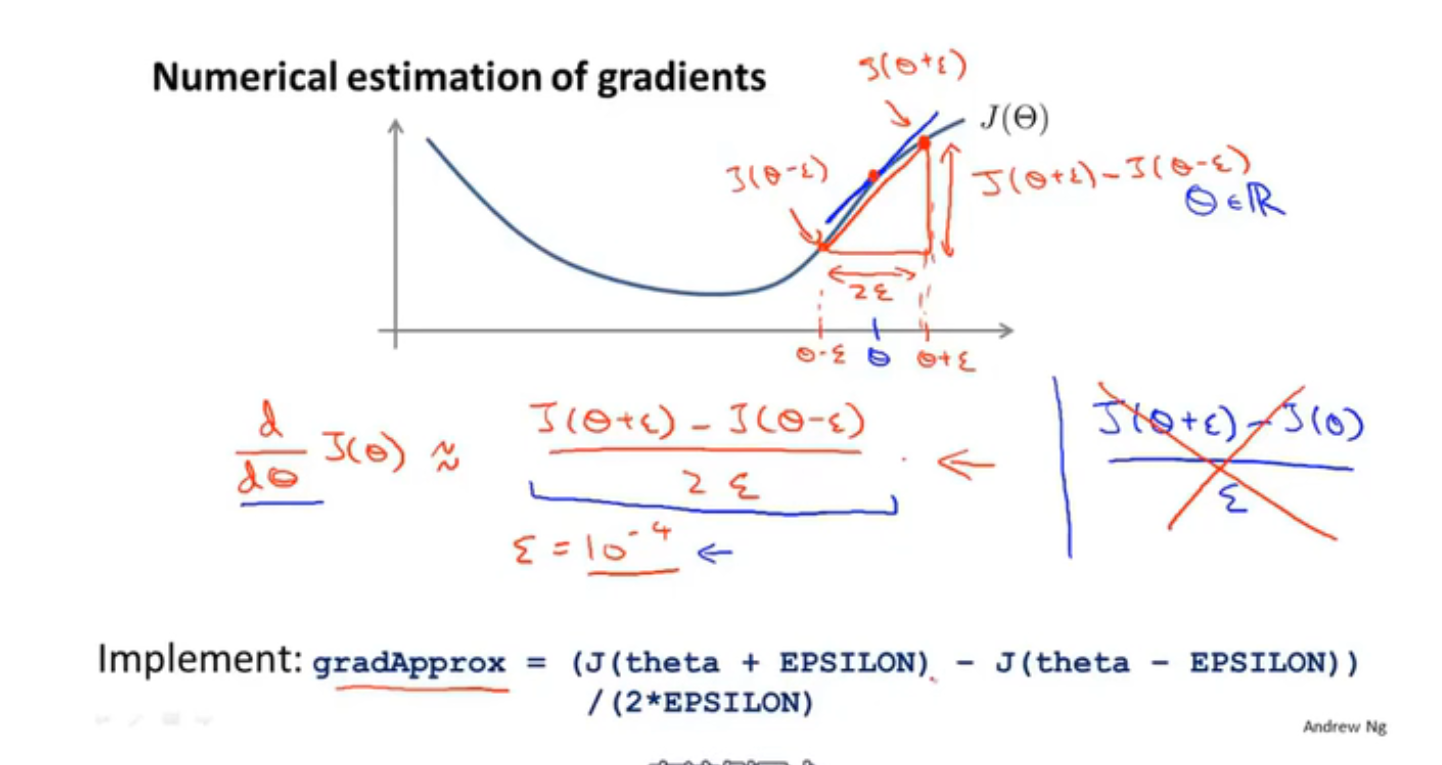
梯度检测
为了防止数值上的问题,一般$\theta$ 不会取太小,常取1e-4
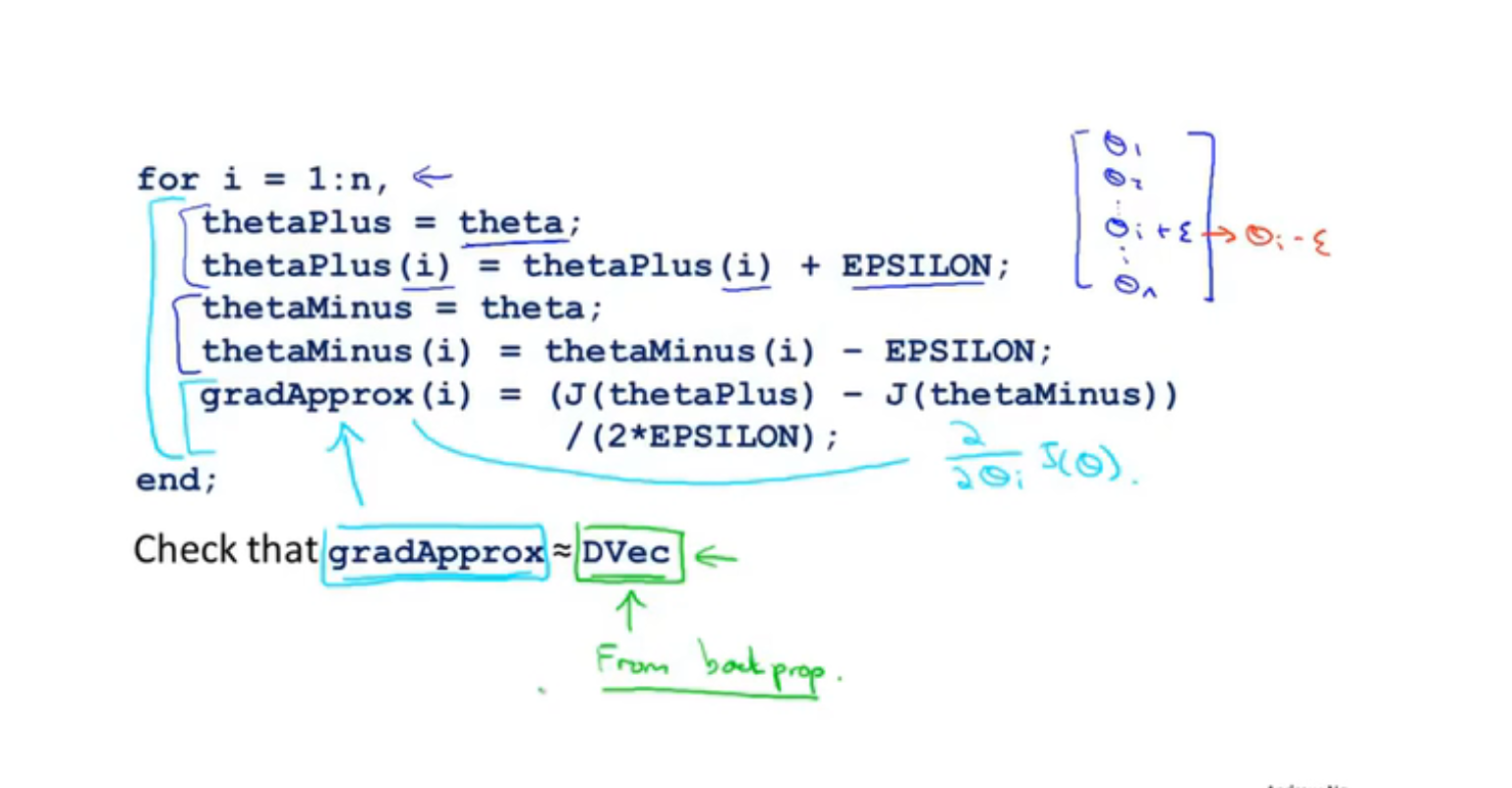
估算偏导数

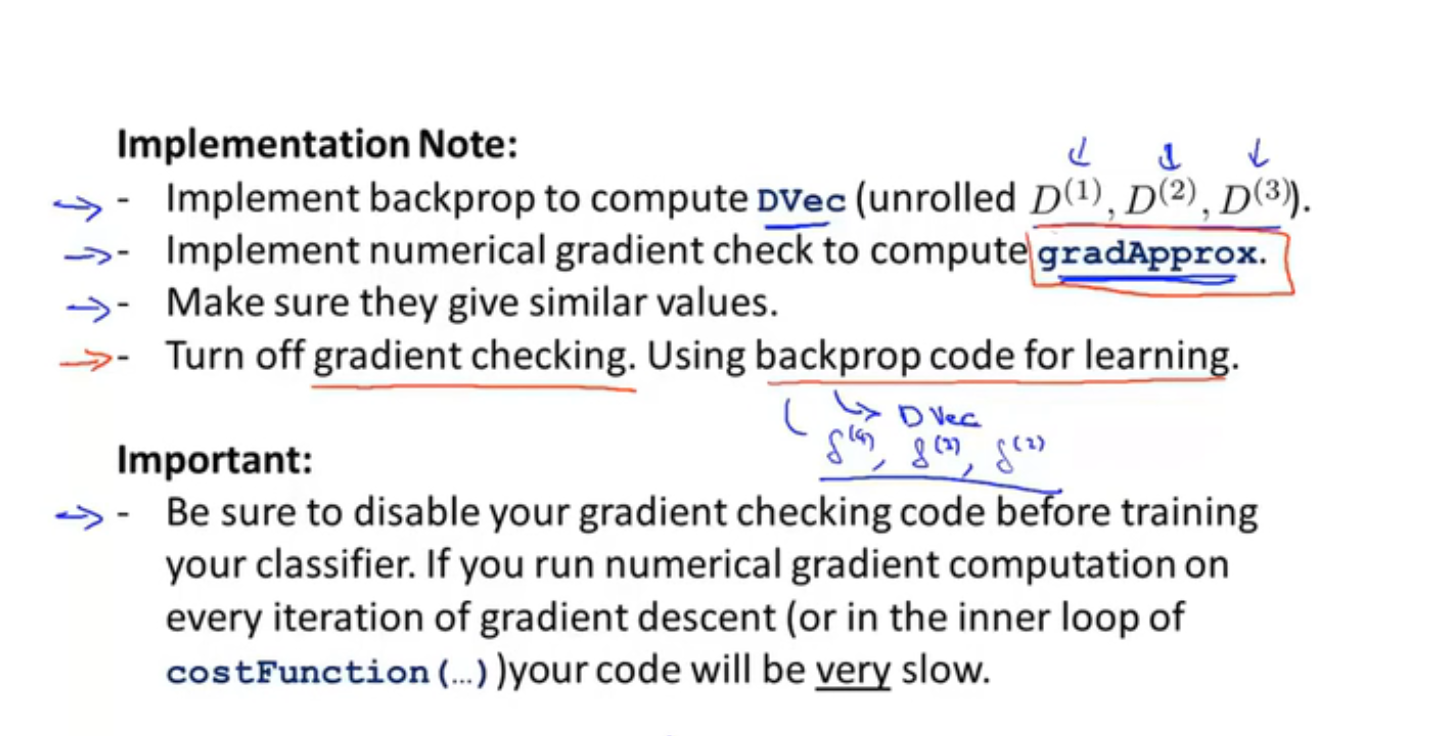
随机初始化

零初始化对神经网络是没有意义的
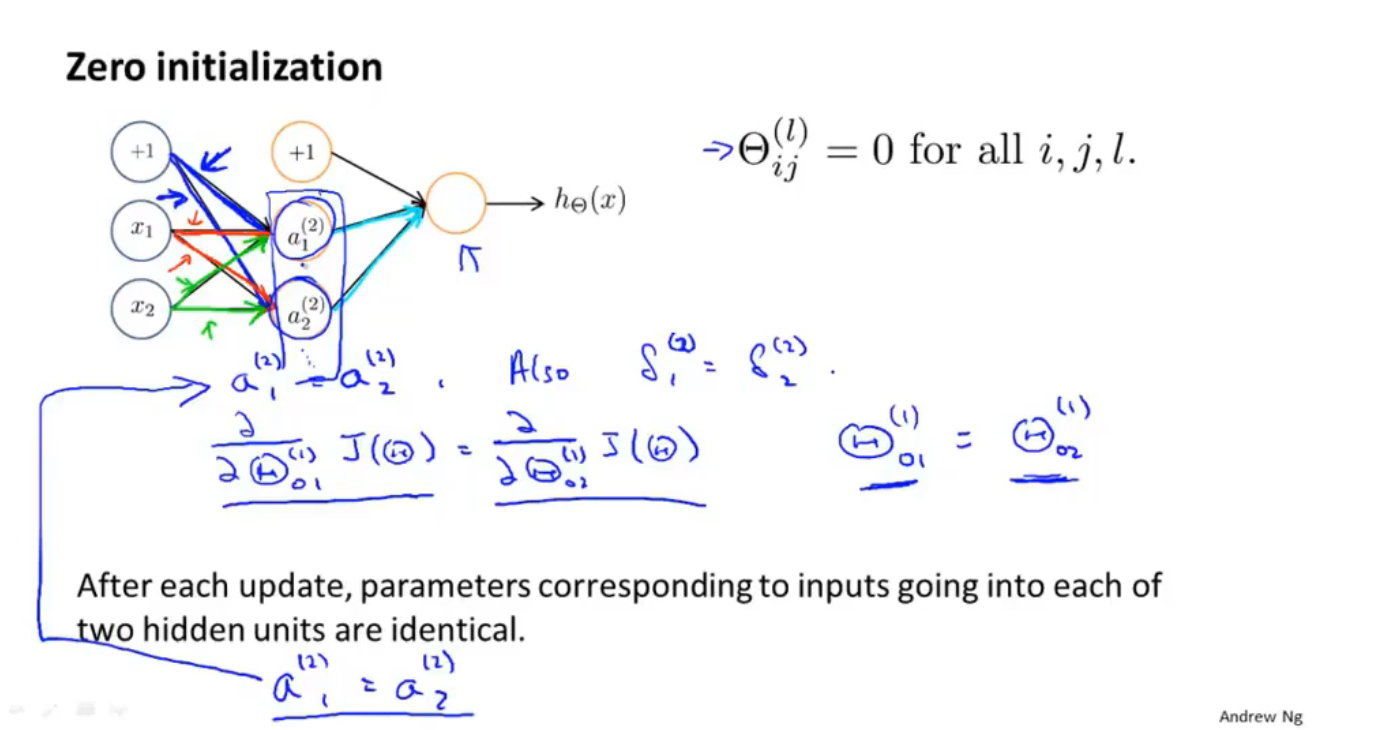

如何训练神经网络


第十节 决定下一步做什么
无所谓的尝试可能浪费很多时间

机器学习诊断法

评估假设
前70%作为训练集,后30%作为测试集



模型的选择、训练、验证、测试
对于测试集拟合的产生的$\theta$新的数据可能拟合效果不好

划分数据集合为 训练集(train 教科书),交叉验证集(cv 课后 作业),测试集(test 期末考试)


用训练集拟合得到$\theta$ ,然后用交叉验证集来计算 J error(泛化误差),选择最小的一个作为d

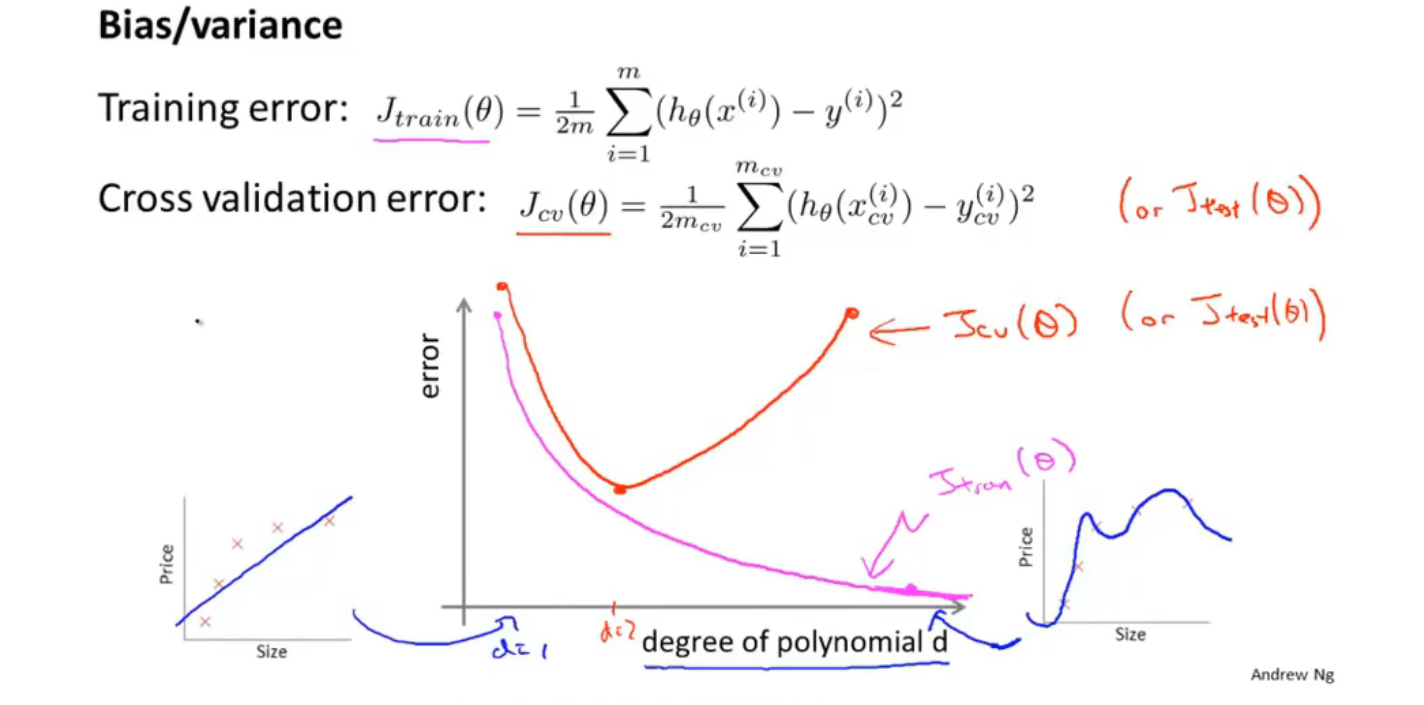
偏差(Bias)与方差(Variance)
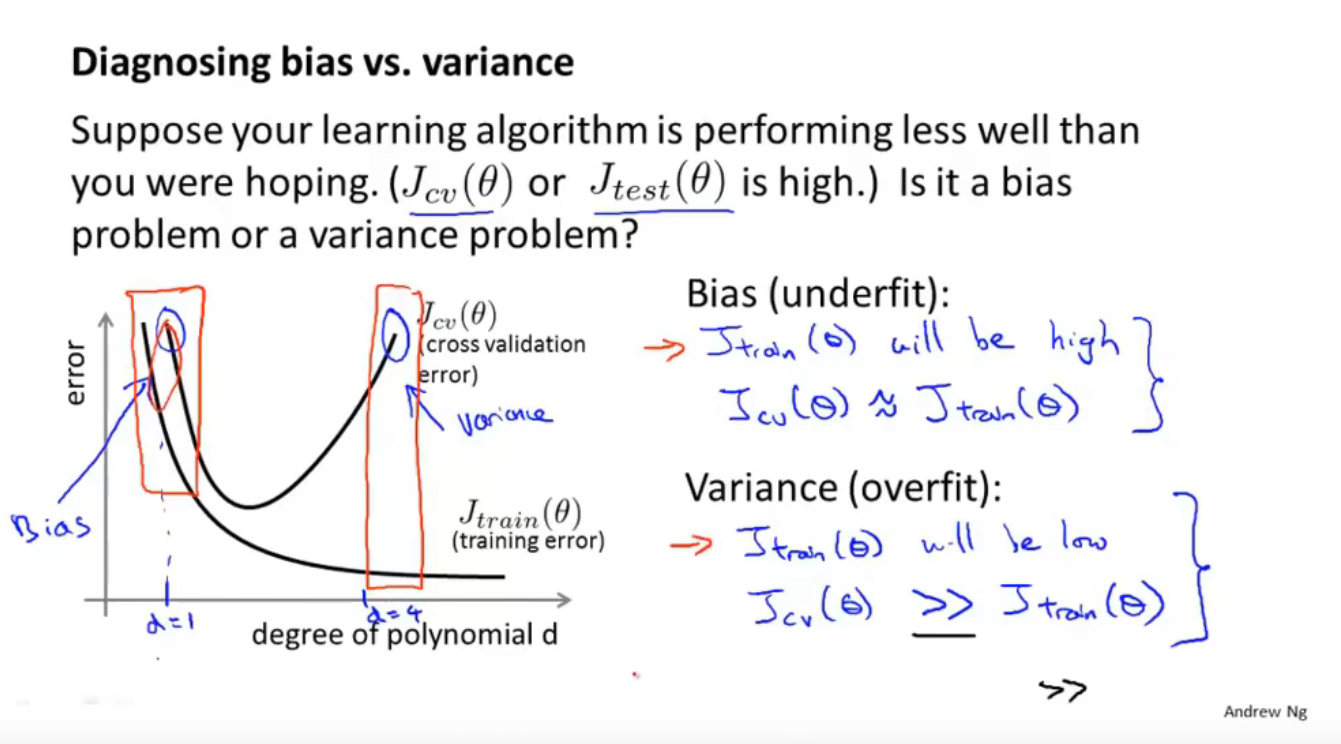
正则化与偏差(欠拟合)、方差(过拟合)
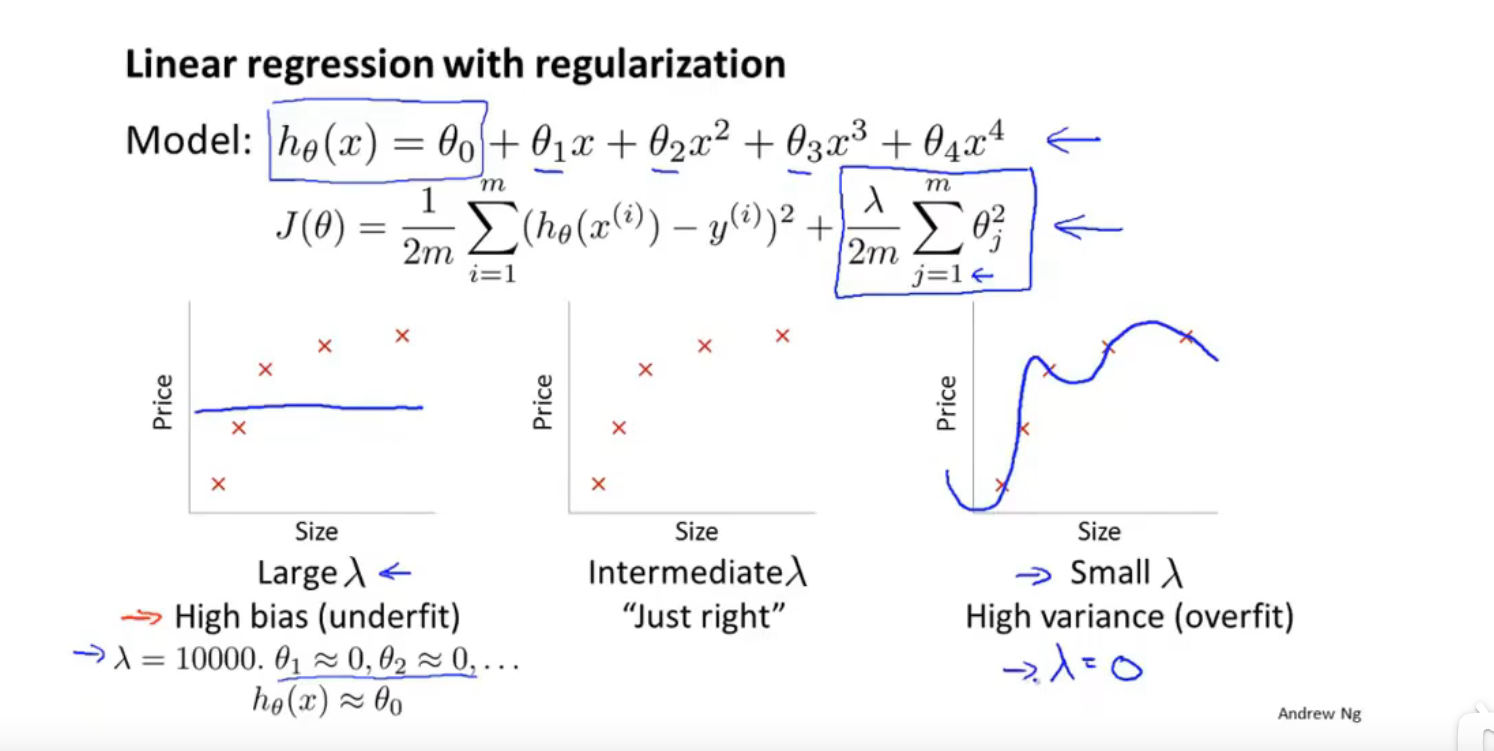
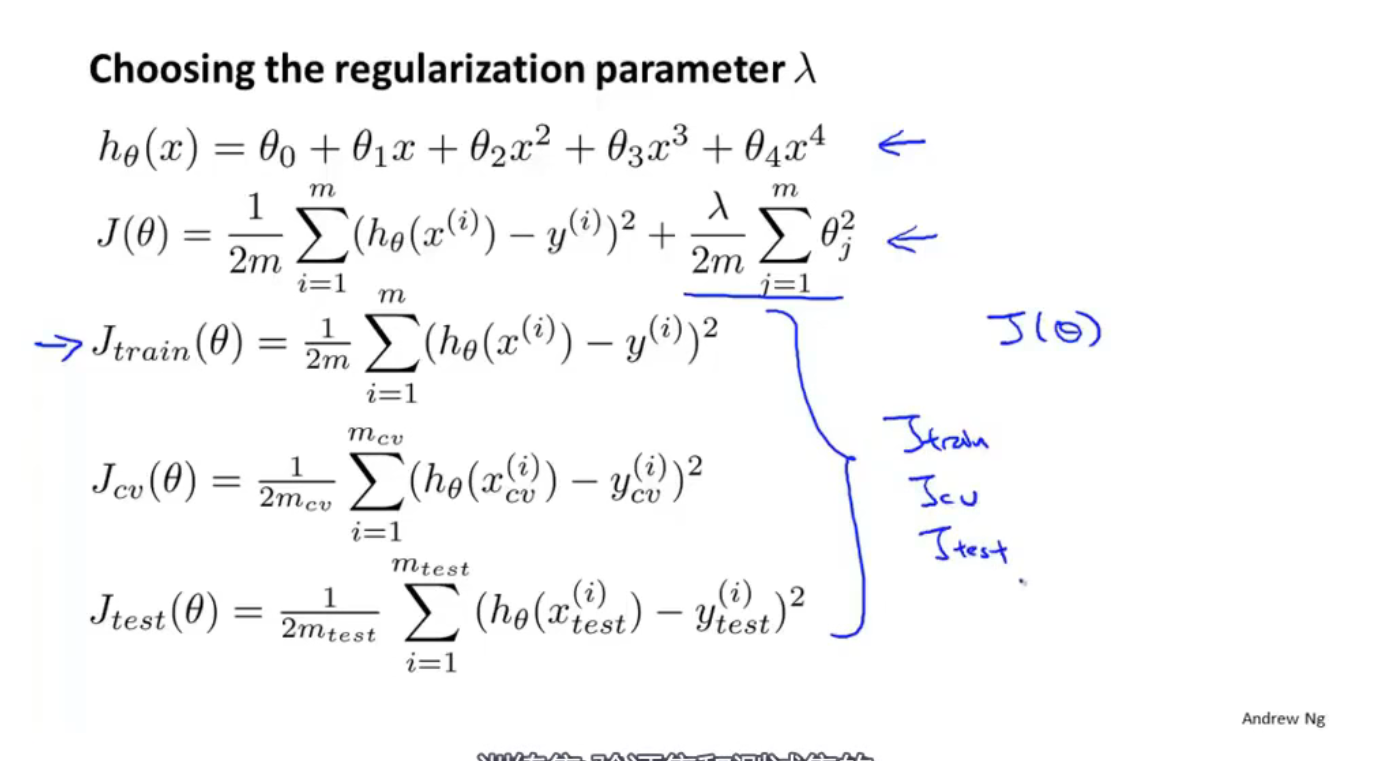
用J(包含正则化项)来求theta,然后为了比较lameda对theta的影响,用Jtrain和Jcv绘制曲线(不包含正则化项)。其实训练时用的是J,而Jtrain和Jcv只是用来画线说明问题


学习曲线绘制
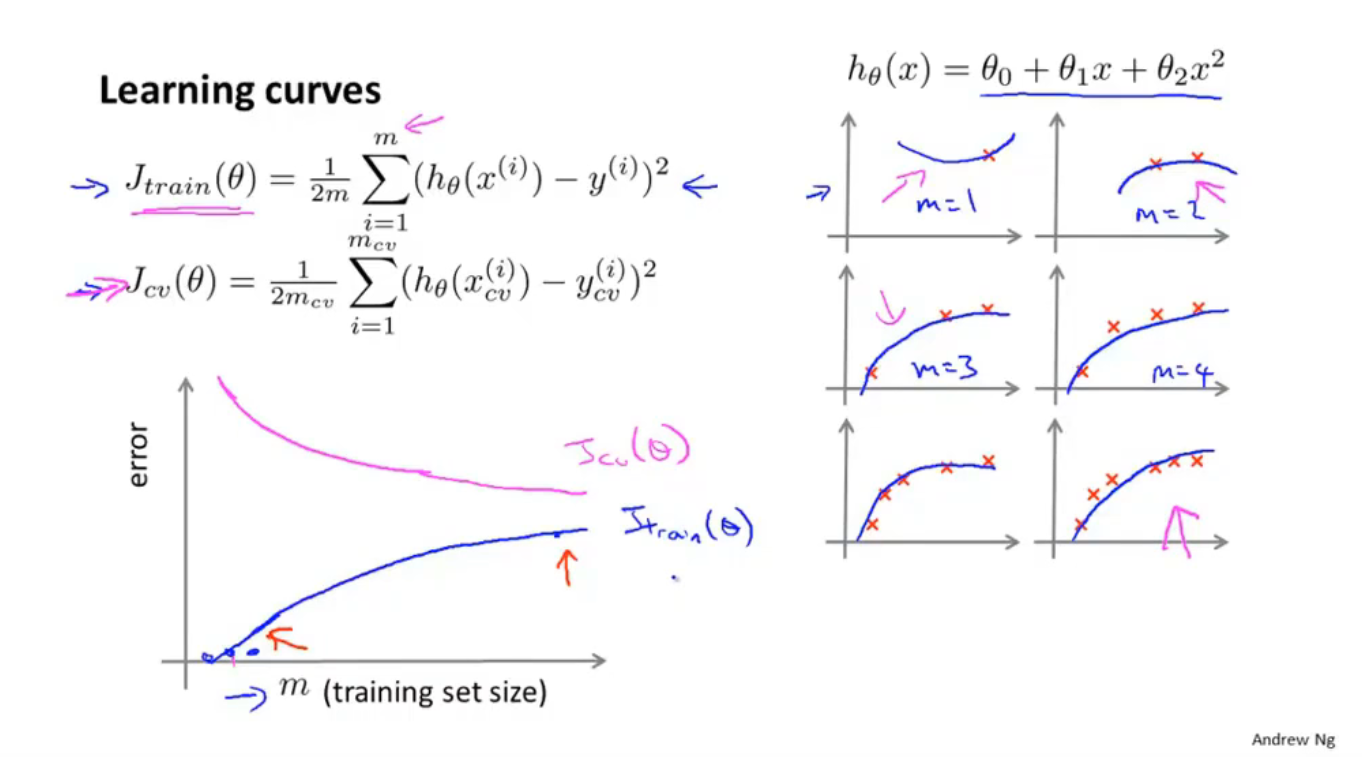
高偏差
高偏差下,训练集大小对于 降低 J error 没大作用

高方差下,增加训练集,对降低J error 是有效的
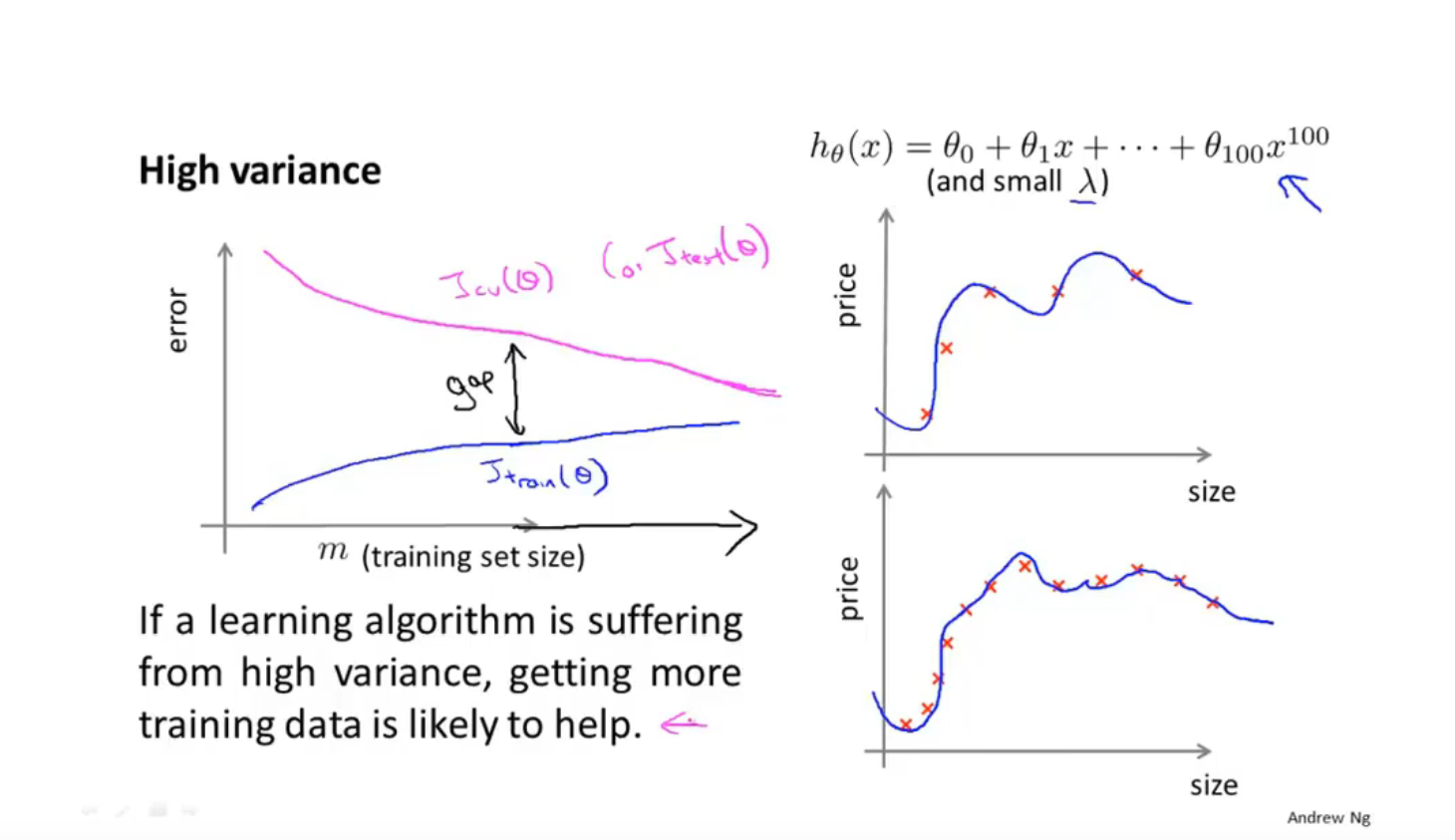
根据学习曲线改进学习方法(尽量不做徒劳工作

第十一节
误差分析
不对称性分类的误差评估
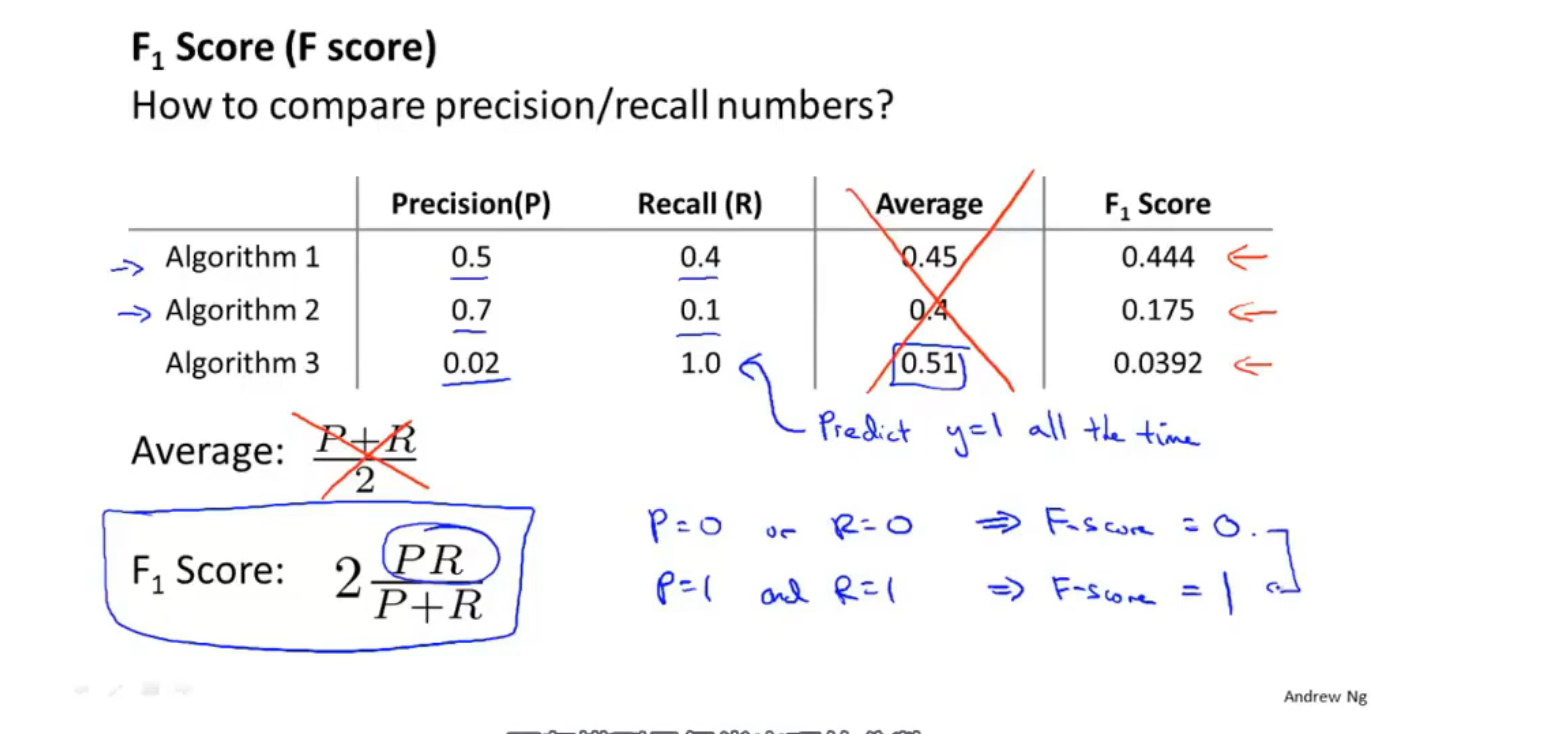
混淆矩阵 & 准确率、精确率、召回率
高的准确率和召回率可以评价一个算法是不是足够好
通过F值来判断算法的好坏
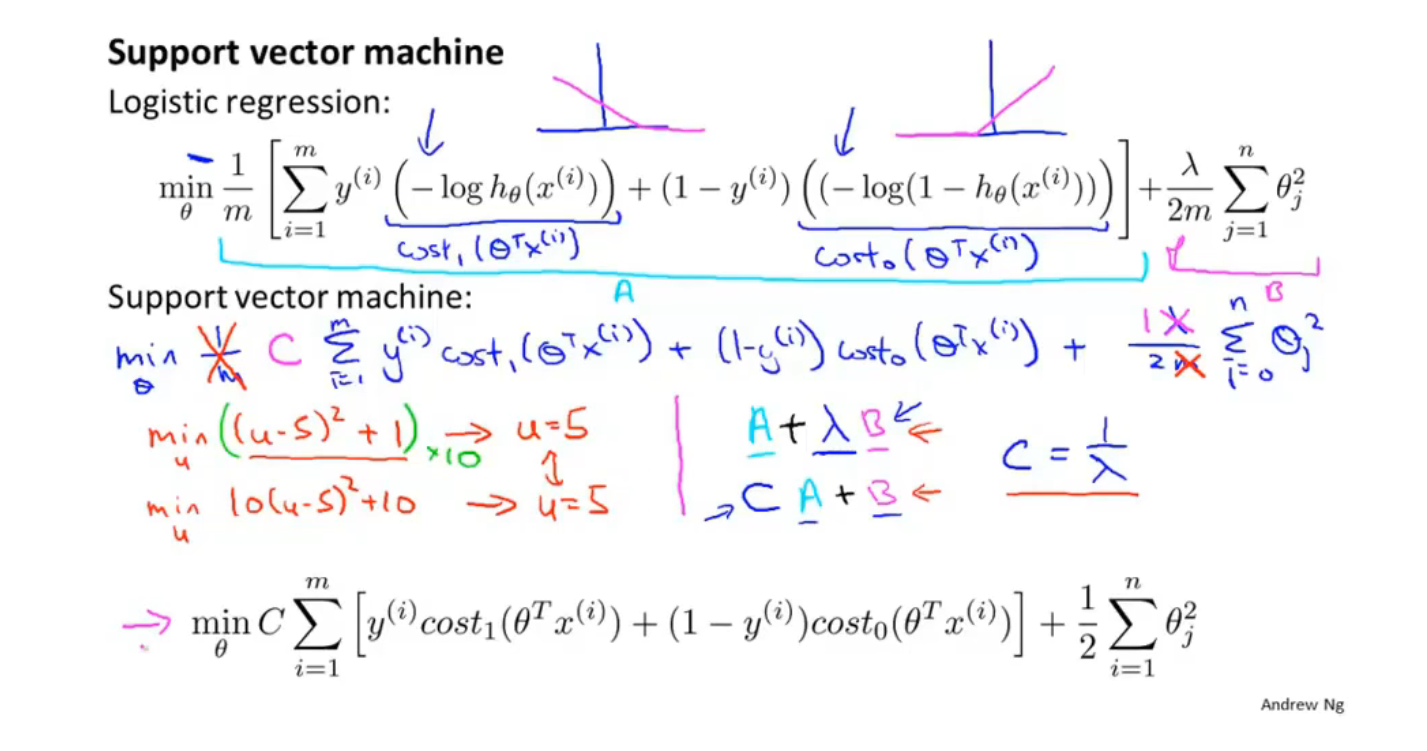
第十二节 SVM
SVM是监督学习算法
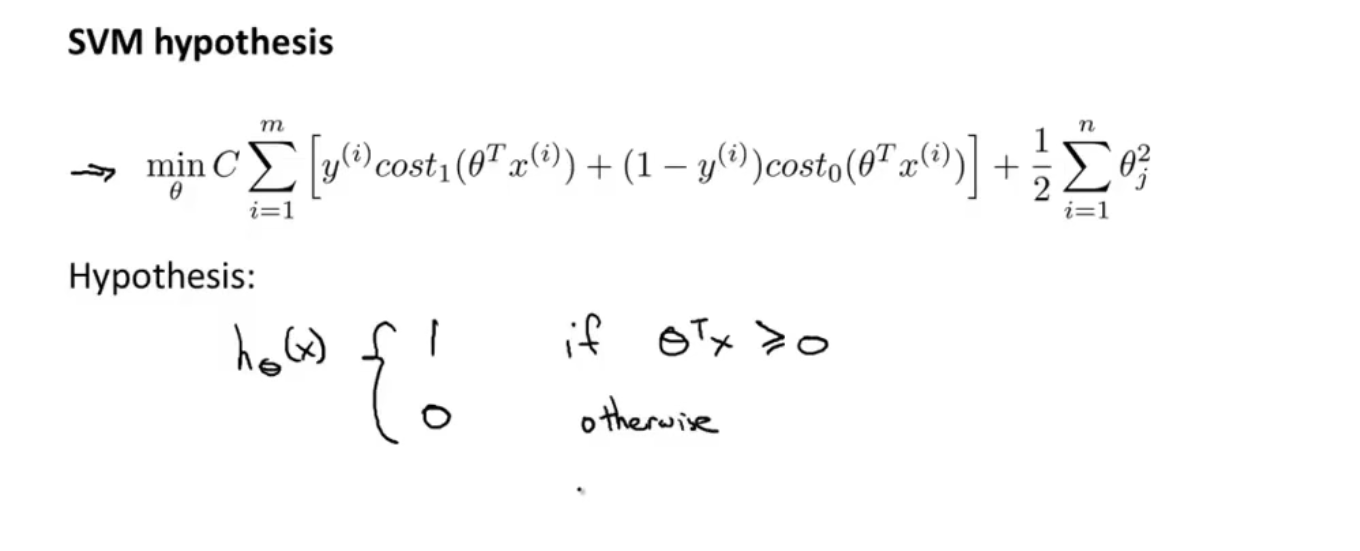
补充的知识点
最小二乘法

相关术语
线性回归 Linear regression
单变量线性回归 Linear regression with one variable
代价函数 Cost Function
平方误差代价函数 Squared error cost function
建模误差 Modeling error
等高线 contour plot 、contour figure
梯度下降 Gradient descent
批处理梯度下降 Batch gradient descent
学习效率 Learning rate
同步更新 simultaneous update
非同步更新 non-simultaneous update
局部最优 local optimum
全局最优 global optimum
全局最小值 global minimum
局部最小值 local minimum
微分项 derivative term
微积分 calculus
导数 derivatives
偏导数 partial derivatives
负导数 nagative derivative
负斜率 nagative slope
收敛 converge
发散 diverge
陡峭 steep
碗型 bow-shaped function
凸函数 convex function
线性代数 linear algebra
迭代算法 iterative algorithm
正规方程组 normal equations methods
梯度下降的泛化 a generalization of the gradient descent algorithm
越过最低点 overshoot the minimum

