第一章 统计学习方法概论
- 赫尔伯特-西蒙对学习的定义:如果一个系统能够通过执行某个进程改进它的性能,这就是学习。按照这一观点,统计学习就是计算机系统通过运用数据及统计方法提高系统性能的机器学习。
统计学习的对象
data :计算机及互联网上的各种数字、文字、图像、视频、音频数据以及它们的组合。
数据的基本假设是同类数据具有一定的统计规律性。
统计学习的目的
用于对数据(特别是未知数据)进行预测和分析。
统计学习的方法
分类:
Supervised learning
Unsupervised learning
Semi-supervised learning
Reinforcement learning
监督学习:
训练数据 training data
模型 model ——- 假设空间 hypothesis
评价准则 evaluation criterion ——– 策略 strategy
算法 algorithm概率图模型
统计学习方法三要素:模型、策略、算法
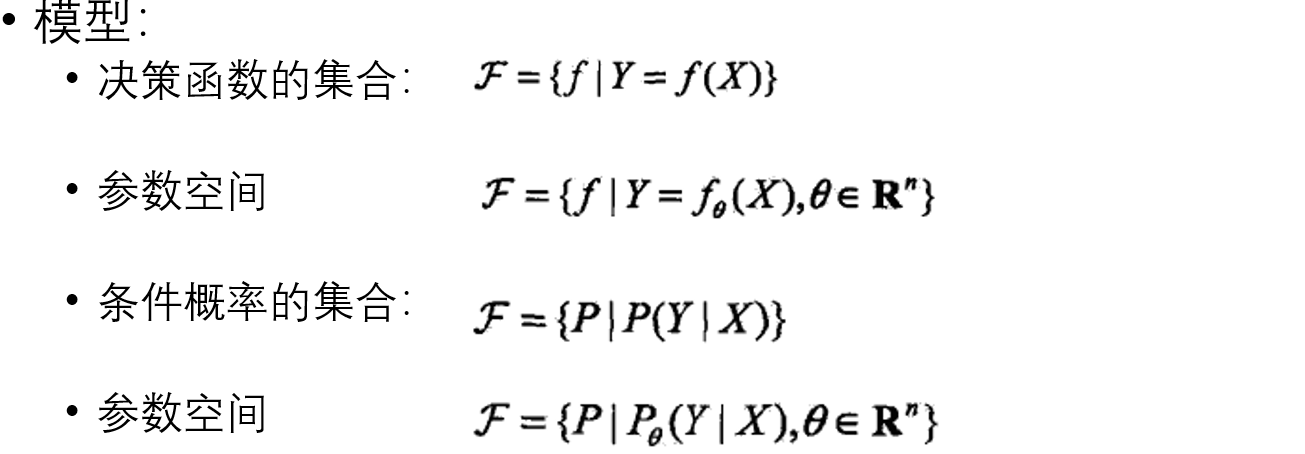



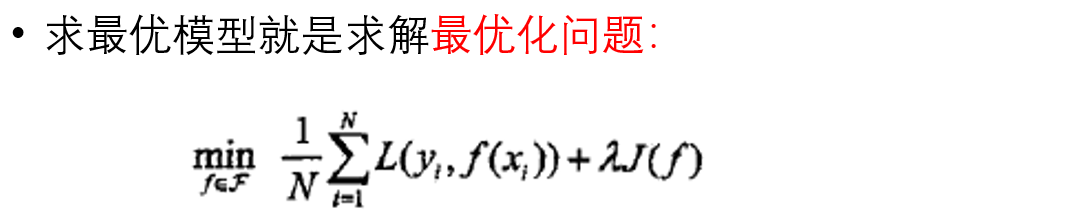
第二章 感知机
感知机学习算法
感知机模型

算法2.1(感知机学习算法的原始形式)

算法2.2(感知机学习算法的对偶形式)


第四章 朴素贝叶斯




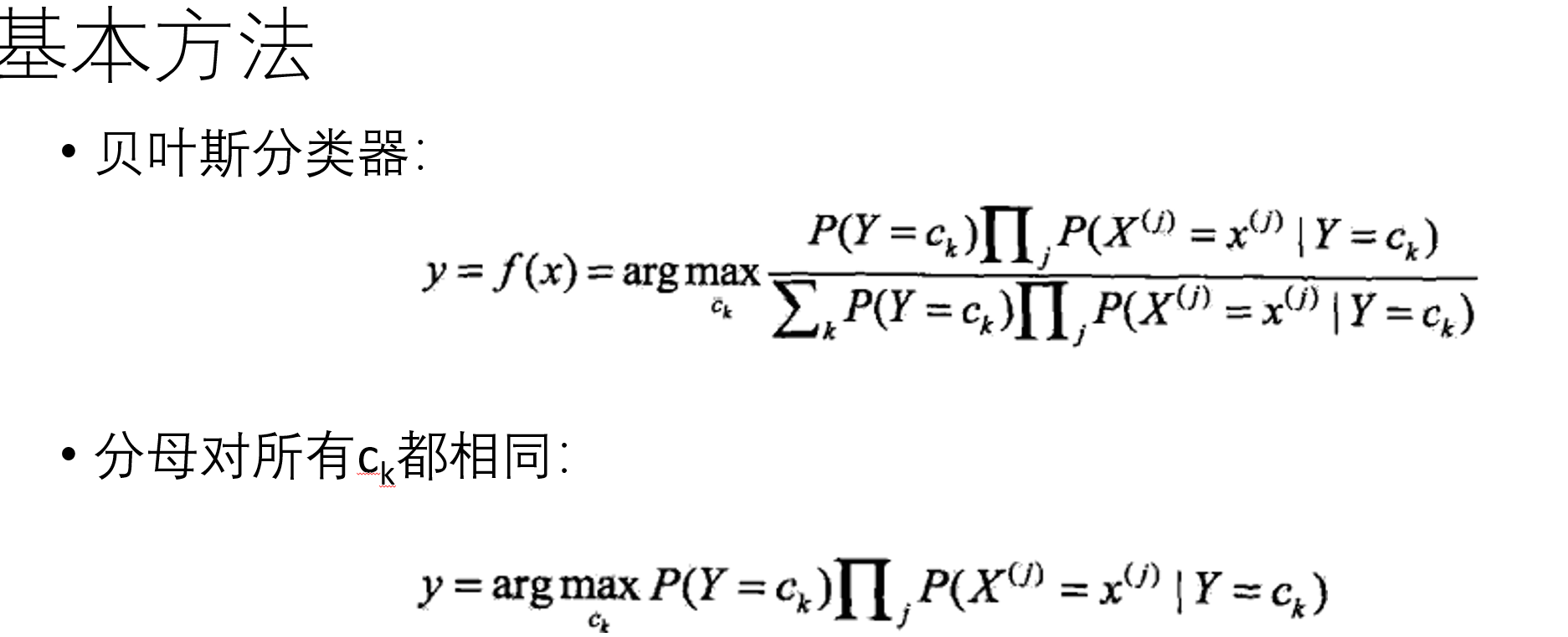
后验概率最大化的含义:朴素贝叶斯法将实例分到后验概率最大的类中,等价于期望风险最小化
朴素贝叶斯法的参数估计:应用极大似然估计法估计相应的概率

用极大似然估计可能会出现所要估计的概率值为0的情况,这时会影响到后 验概率的计算结果,使分类产生偏差.解决这一问题的方法是采用贝叶斯估计。

式中$\lambda>=0$,等价于在随机变量各个取值的频数上赋予一个正数$\lambda>0$,$\lambda=0$时就是极大似然估计。通常取$\lambda=1$,这时称为拉普拉斯平滑。

