实验
消融实验
消融实验类似于“控制变量法”。
假设在某目标检测系统中,使用了A,B,C,取得了不错的效果,但是这个时候你并不知道这不错的效果是由于A,B,C中哪一个起的作用,于是你保留A,B,移除C进行实验来看一下C在整个系统中所起的作用。
数学名词
欧式空间与黎曼空间
fisher information matric

用极大似然估计进行参数估计

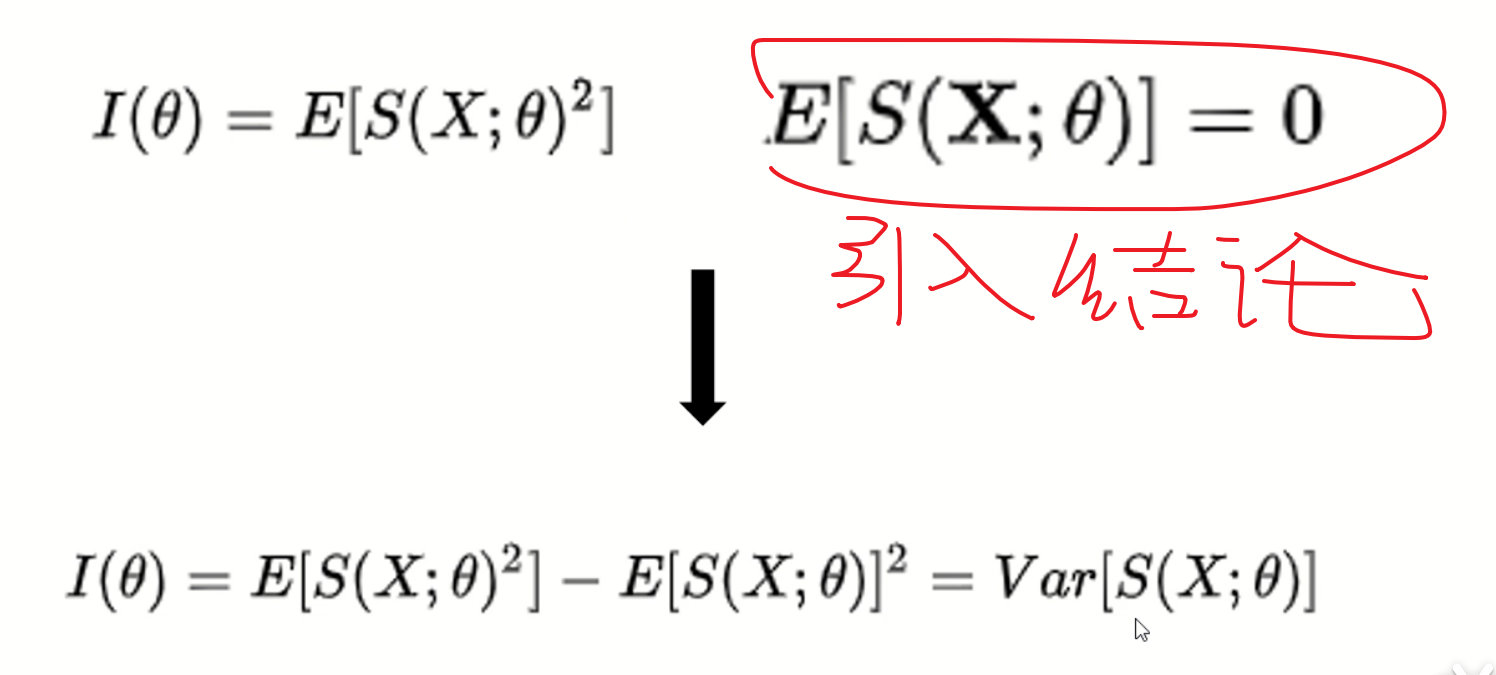
证明:
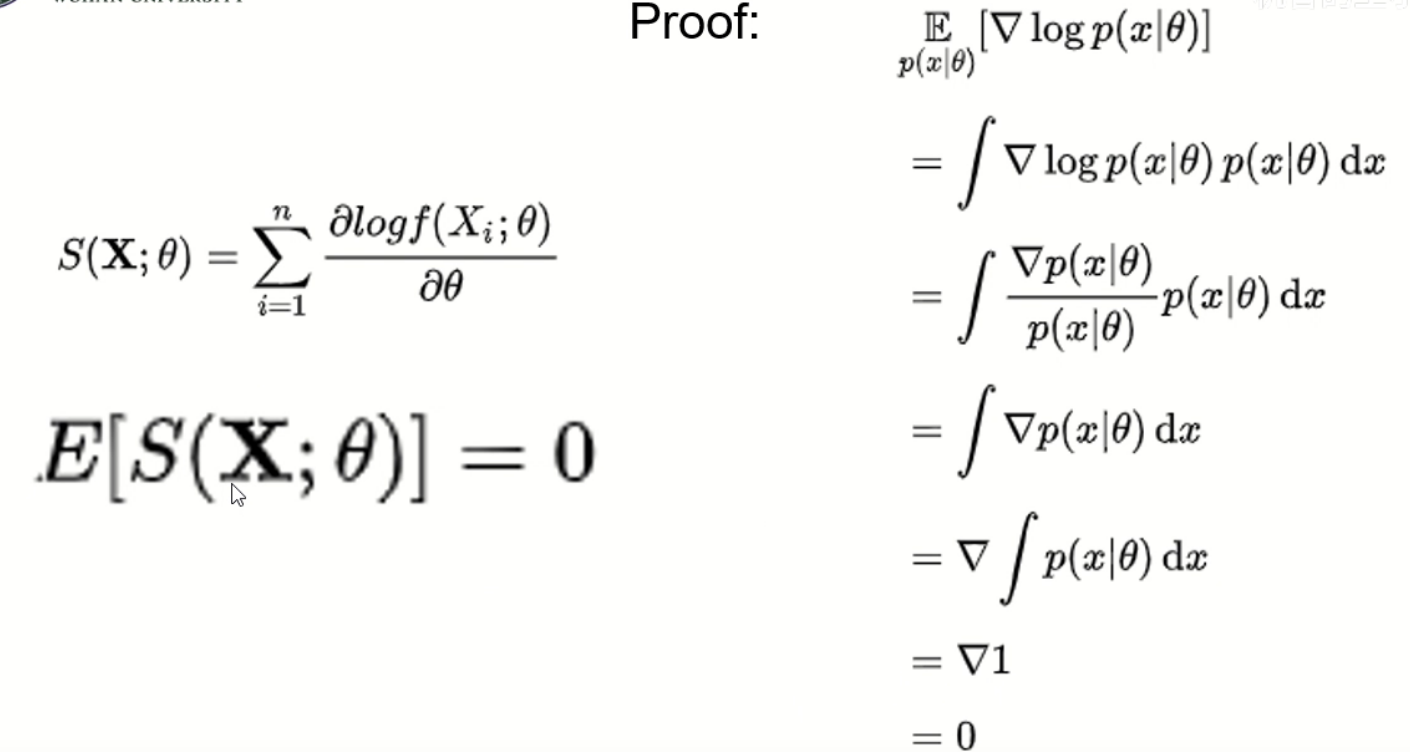
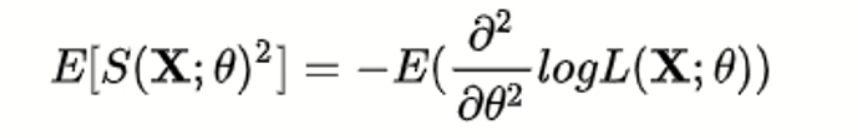
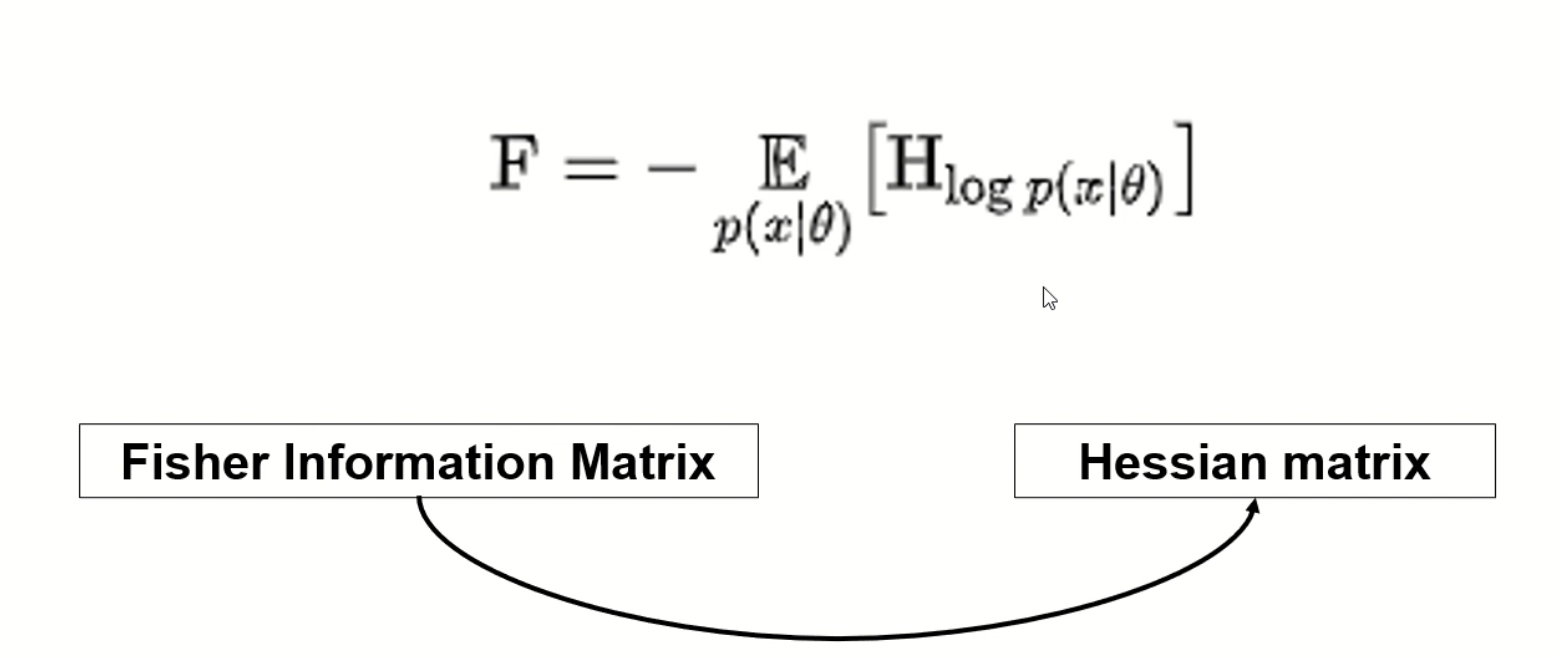
KL散度
用来衡量两个分布之间的距离(在黎曼空间上;欧式空间不适合衡量两个分布之间的距离),又被称为相对熵
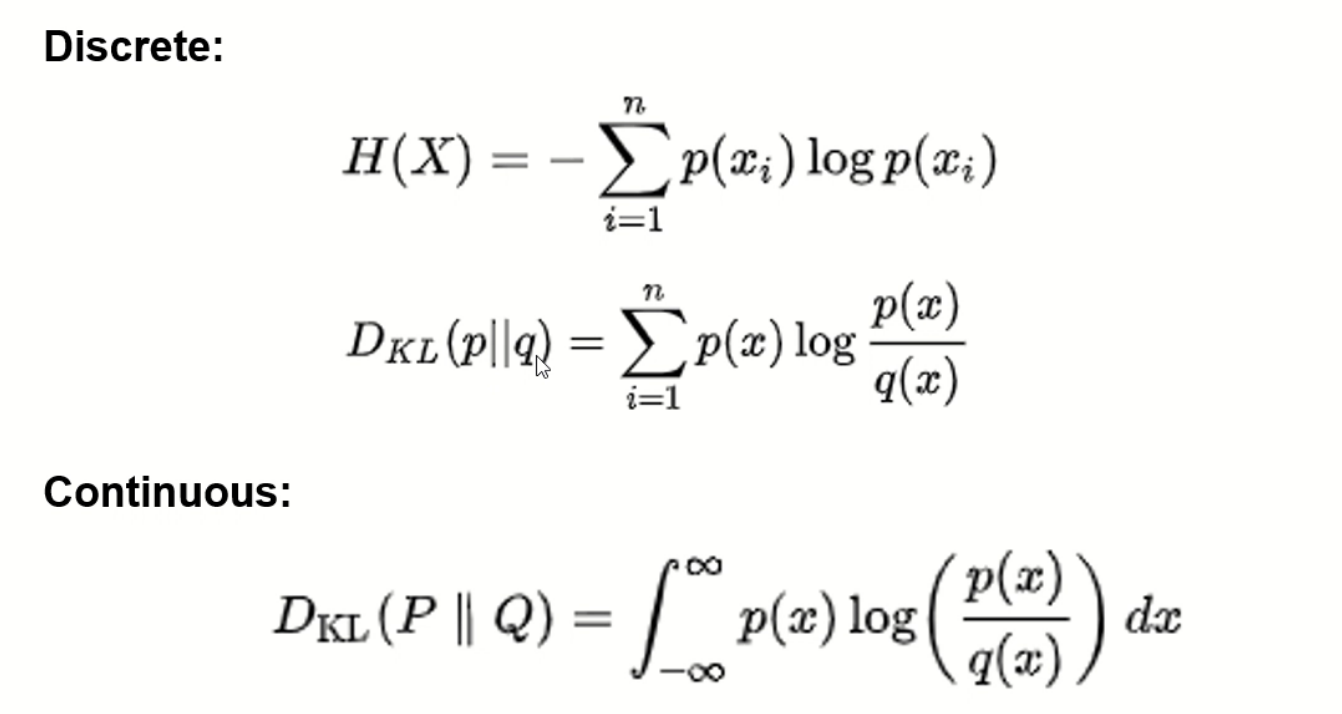

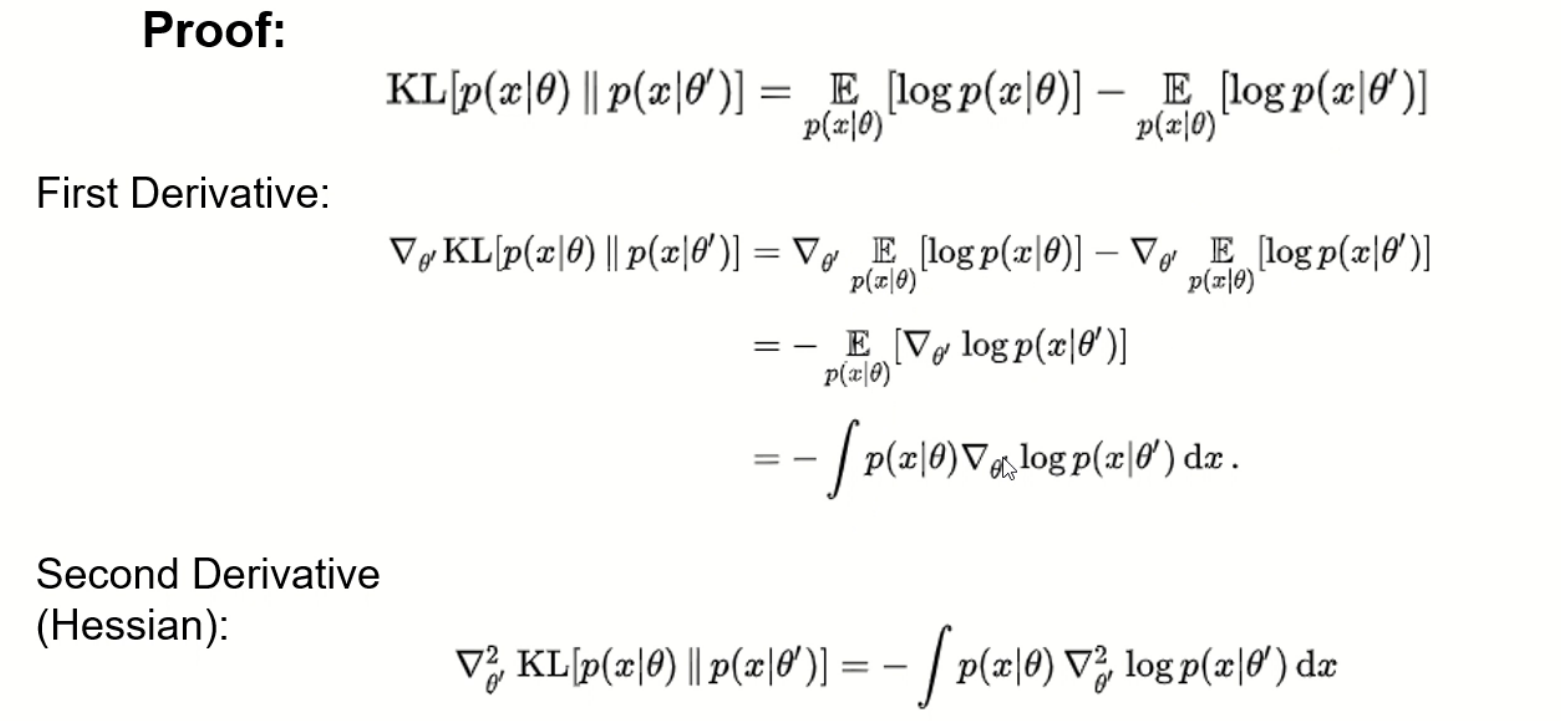
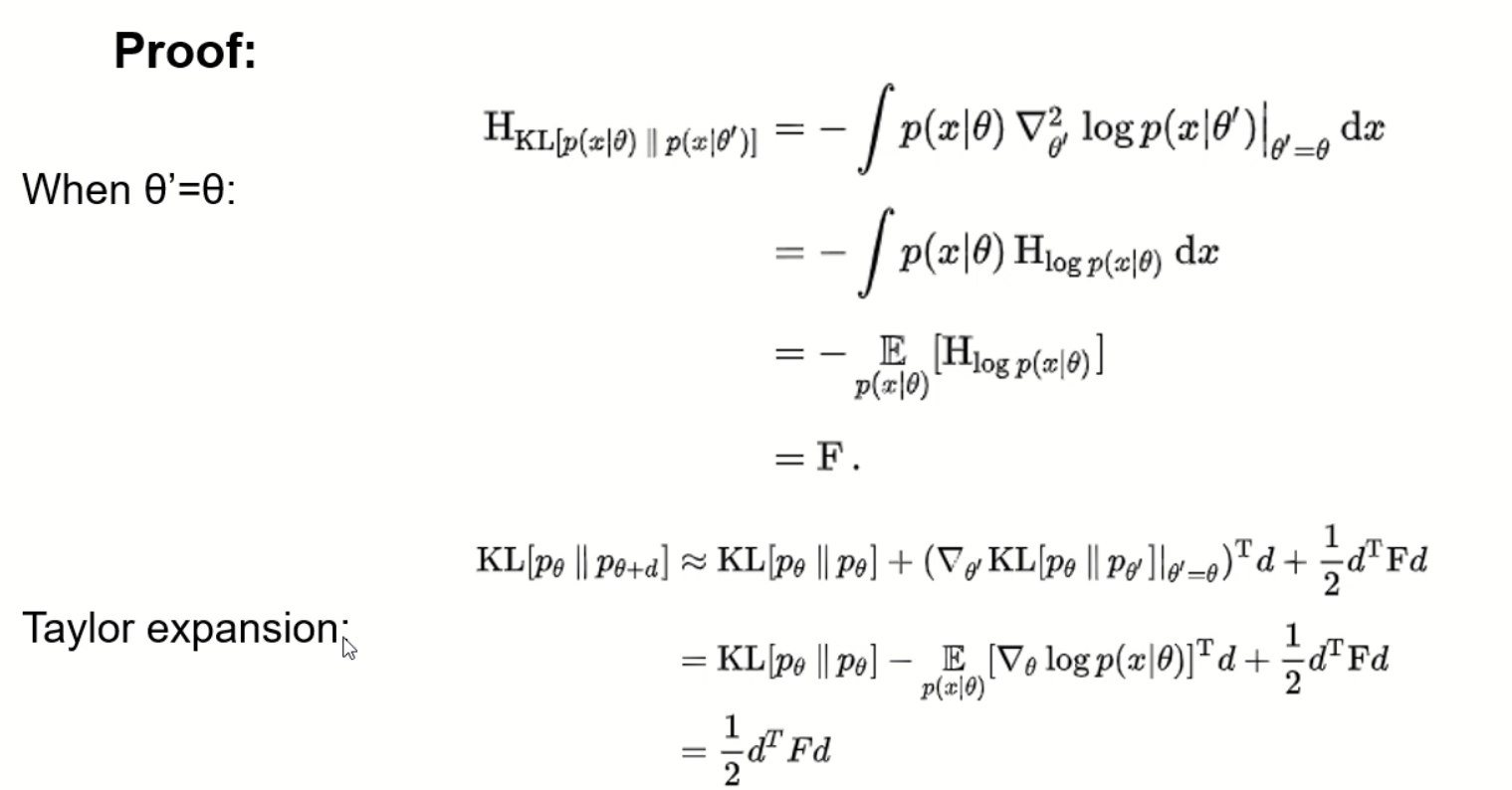
自然策略梯度法
因果熵
因果熵(Causal entropy)是一种用于度量因果关系复杂度的概念。它是因果图中节点的不确定性或混乱程度的度量,用于描述因果图中的信息量。
在因果推断中,因果关系通常用有向无环图(DAG)来表示,其中每个节点代表一个变量,边表示变量之间的因果关系。因果熵可以用来衡量这个因果图中每个节点的混乱程度或者不确定性,即它在给定其他节点的值后仍然存在多少不确定性。
具体来说,假设 $X$ 是一个节点,它的因果熵可以表示为:
$$H(X|Pa_X)$$
其中 $Pa_X$ 表示 $X$ 的父节点集合,$H(X|Pa_X)$ 表示在已知 $Pa_X$ 的取值时,$X$ 的不确定性。因果熵越高,表示该节点的取值在因果图中的影响越难以理解和预测,因此它对于因果分析和预测问题非常有用。
因果熵可以用条件熵的概念来计算。具体来说,假设 $X$ 是一个节点,它的父节点集合为 $Pa_X$,则 $X$ 的因果熵可以表示为:
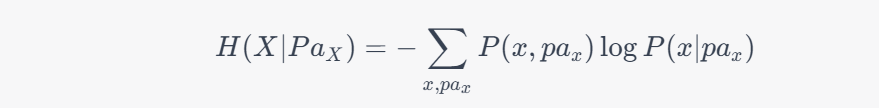
其中 $x$ 是 $X$ 取值的一个可能状态,$pa_x$ 是 $X$ 的父节点取值的可能状态,$P(x, pa_x)$ 是 $X$ 和它的父节点的联合概率分布,$P(x|pa_x)$ 是在给定 $X$ 的父节点取值为 $pa_x$ 的情况下,$X$ 取值为 $x$ 的条件概率。
为了计算 $X$ 的因果熵,我们需要首先估计 $P(x, pa_x)$ 和 $P(x|pa_x)$。对于离散变量,可以通过统计频率来估计这些概率分布。对于连续变量,可以使用概率密度函数或者核密度估计等方法来估计这些概率分布。
当计算整个因果图的因果熵时,可以将每个节点的因果熵加起来,得到整个因果图的因果熵:
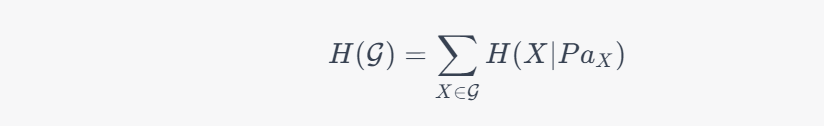
其中 $\mathcal{G}$ 表示整个因果图。因果熵越高,表示因果图的复杂度越高,因此对于因果推断和预测等问题来说,应该选择具有最小因果熵的模型。
果熵作为一种度量因果关系复杂度的概念,在因果推断和因果关系分析中具有广泛的应用。以下是因果熵的一些应用:
- 帮助选择最优的因果模型:因果熵可以用于选择最优的因果模型,即选择具有最小因果熵的模型,这个模型能够最好地解释数据的因果关系。
- 帮助识别因果关系:因果熵可以用于识别因果关系,即当一个节点的因果熵高于其它节点时,它可能是因果图中最重要的节点之一,因此它可以被认为是更可能的因果因素。
- 优化因果图:因果熵可以帮助优化因果图,例如删除不必要的节点或边,以减少因果图的复杂性和提高模型的准确性。
- 检测因果效应:因果熵可以用于检测因果效应,即计算一个因果关系是否在给定数据中有足够的信息量来支持该因果关系的存在。
- 因果关系预测:因果熵可以用于预测因果关系,即通过分析数据中的因果关系,识别潜在的因果关系,从而对未来的事件进行预测。
总之,因果熵是一种非常有用的概念,可以帮助我们更好地理解和应用因果关系,从而提高因果推断和预测的准确性和可靠性。

