强化学习的数学原理

写在前面—— ——对于强化学习的建议

• 不要有追求速成的想法
• 对于自己的目标要分类合理的时间

Introduction

经典书籍

课程目的

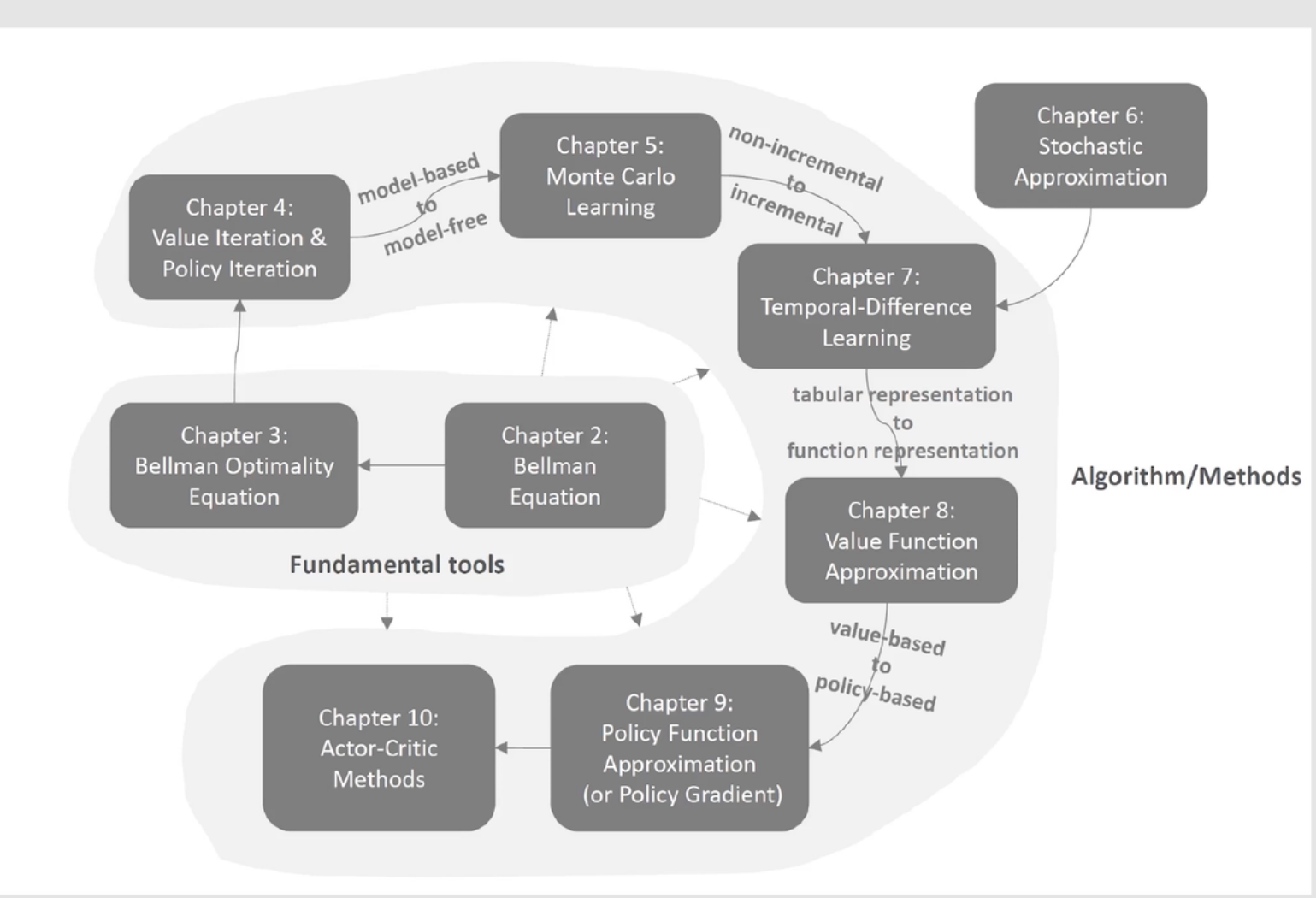
贝尔曼公式

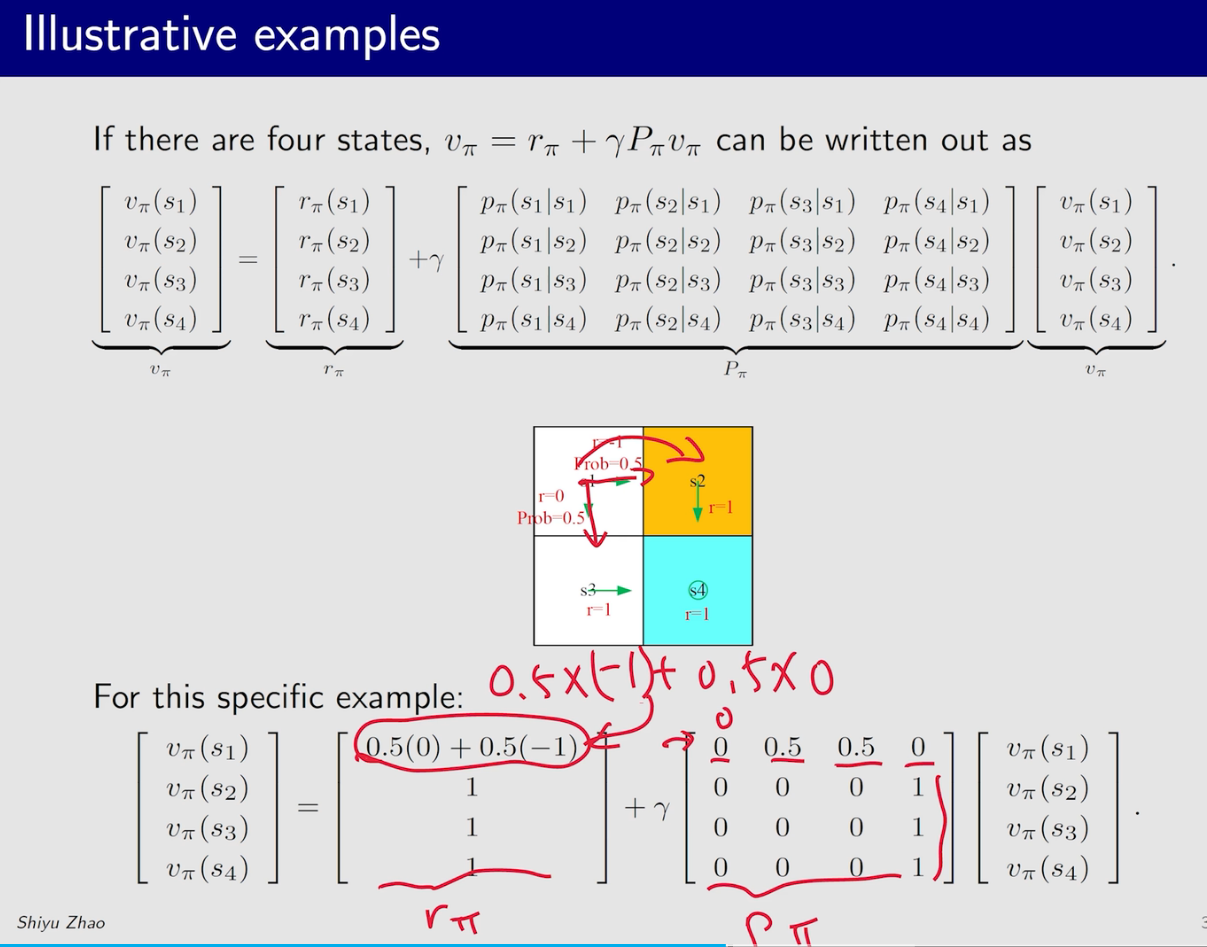
通过计算state value来评价策略的好坏

动作价值函数

从下面的几个公式可以看出，state value 和action value 是可以相互推导的

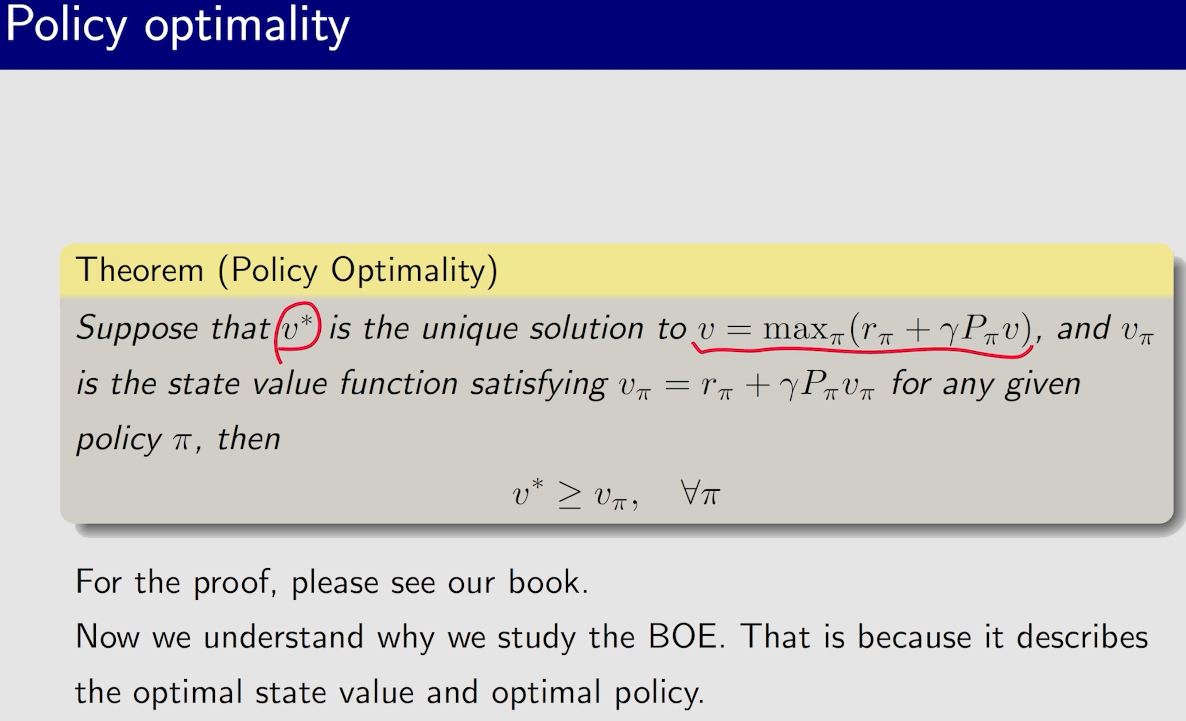
贝尔曼最优公式

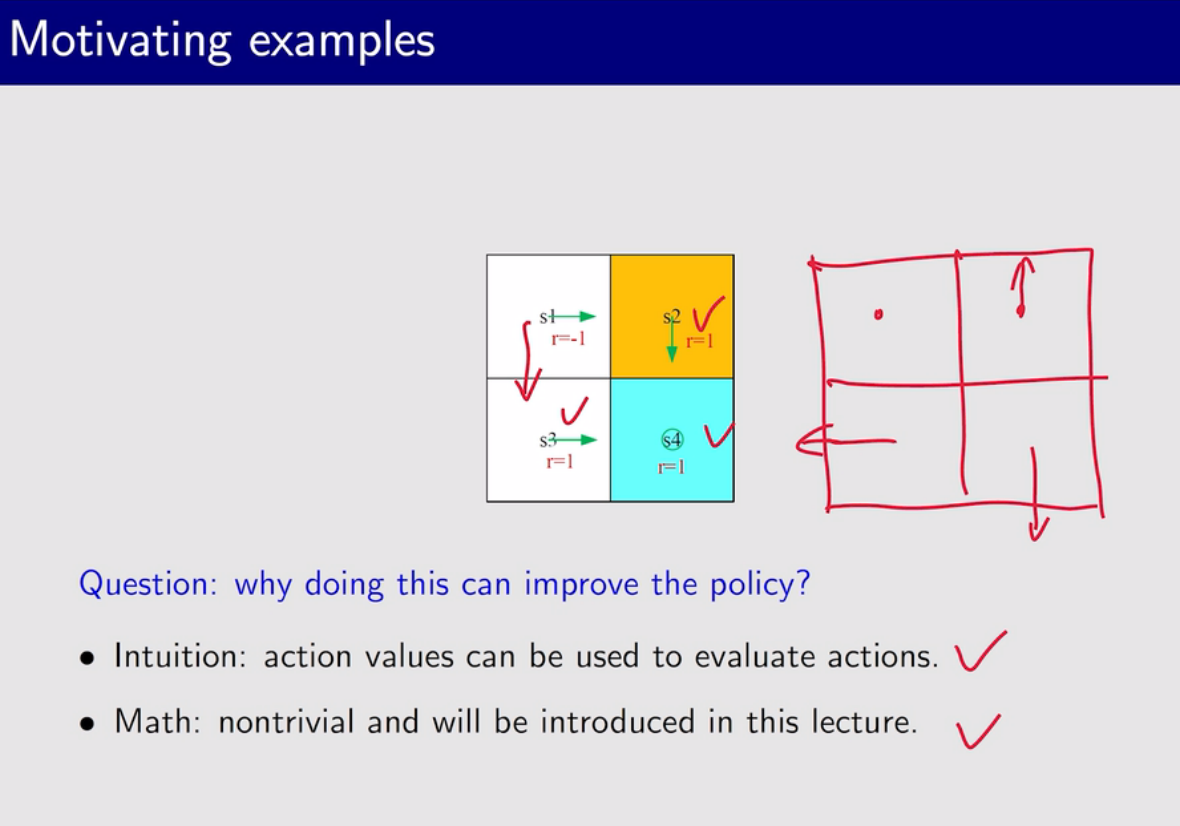
我们要去求解这个优化问题，得到最优的$\pi$

定理求解

$$x=f(x)$$

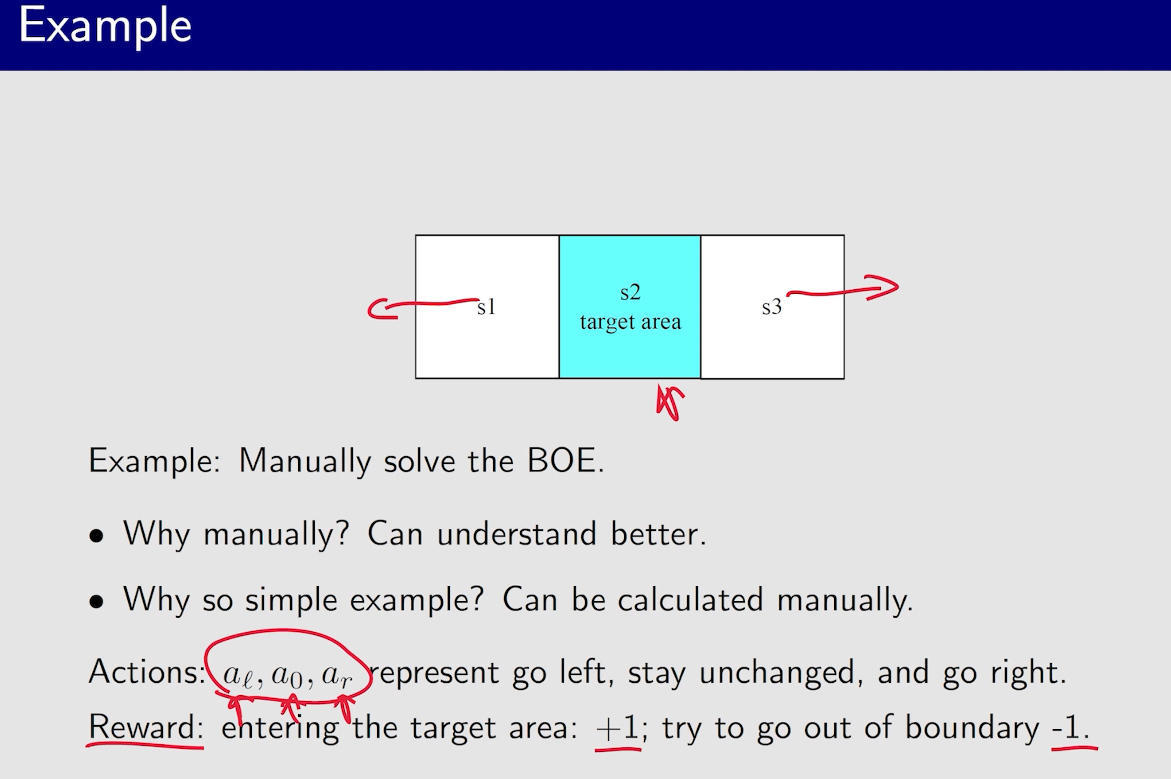
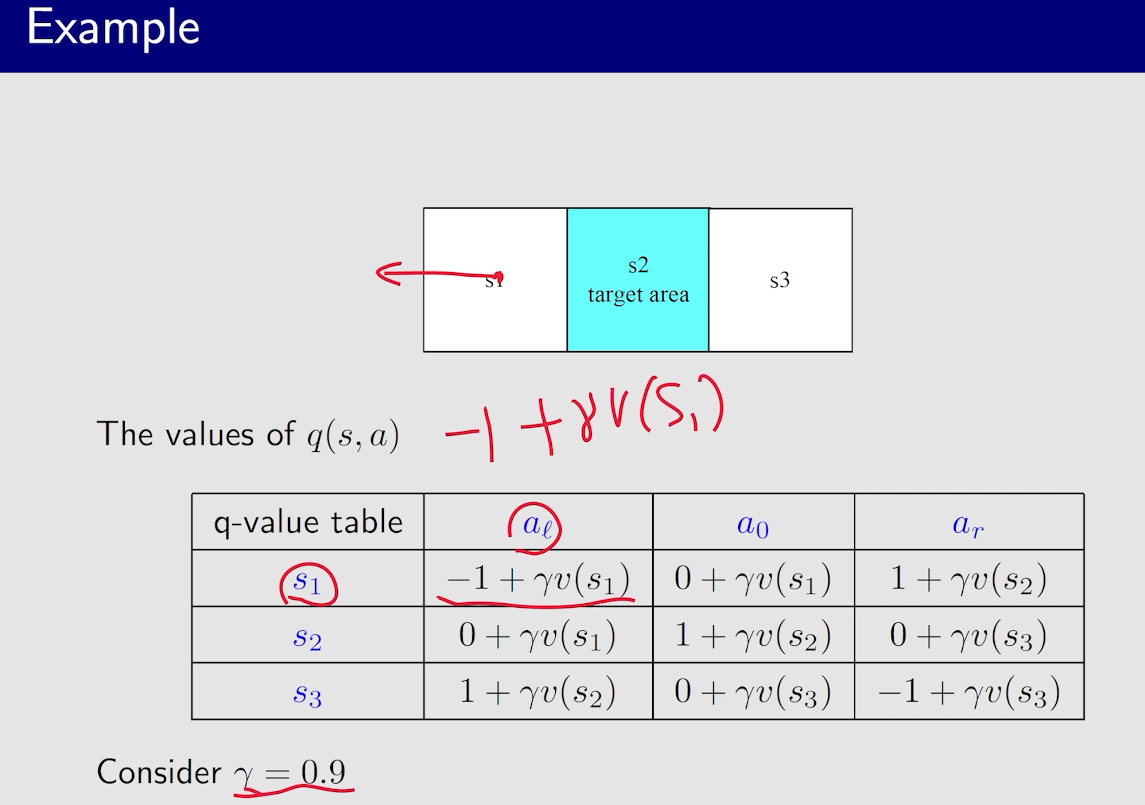
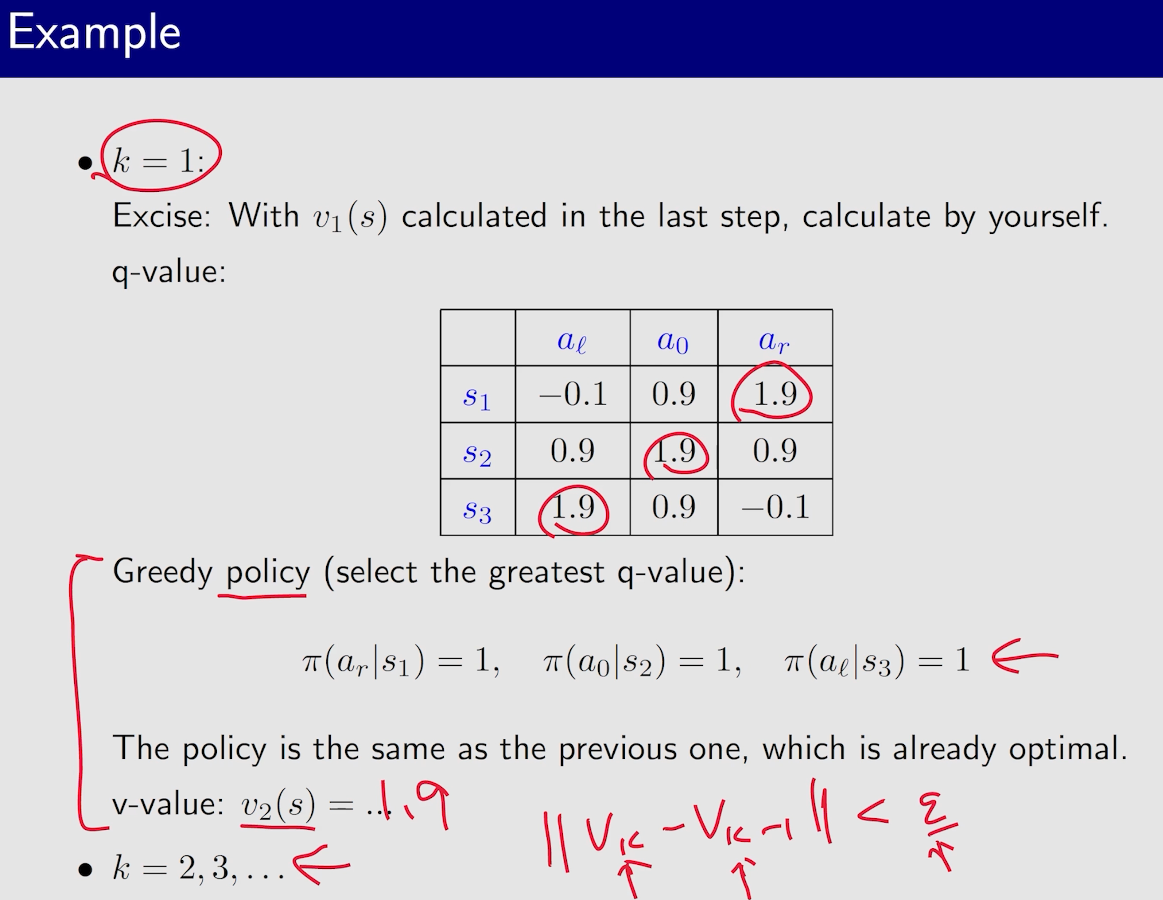
虽然下面例子中，策略已经达到最优，但是state value还没有达到最优，所以需要继续迭代

迭代不能无穷的进行下去，所以需要有终止条件，常见的是$|v_k-v_{k+1}|<\epsilon$

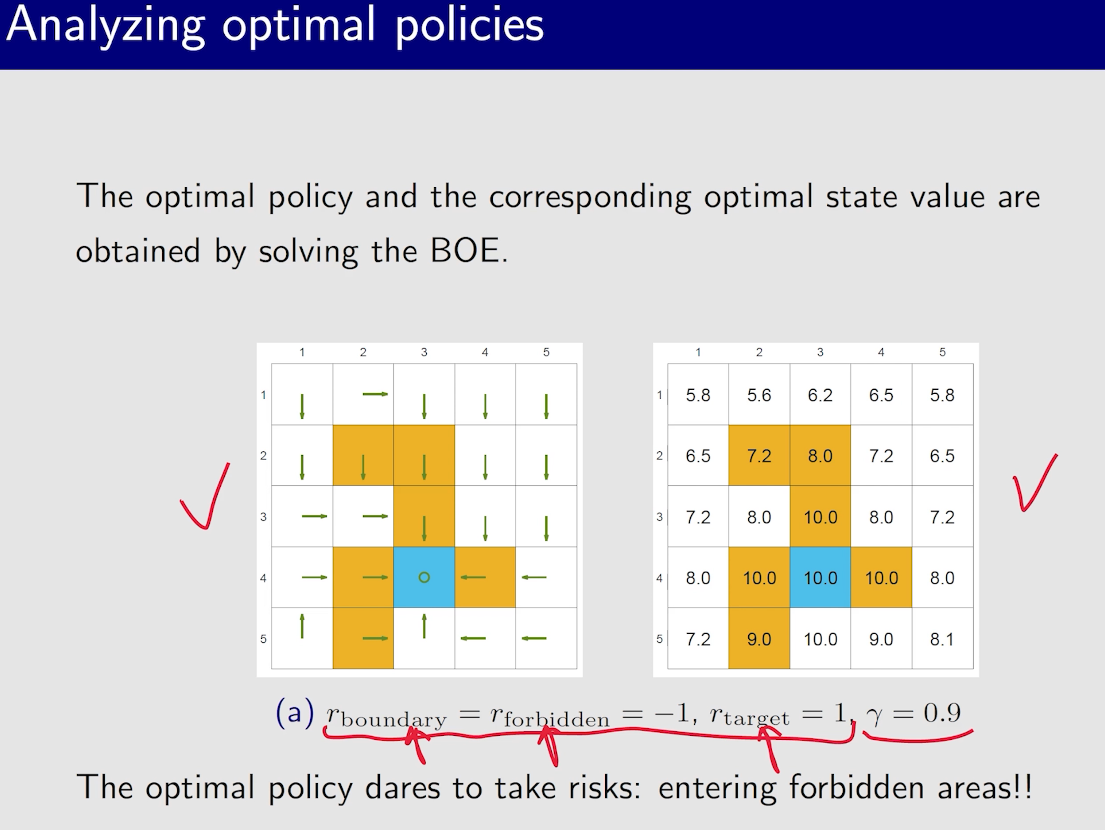
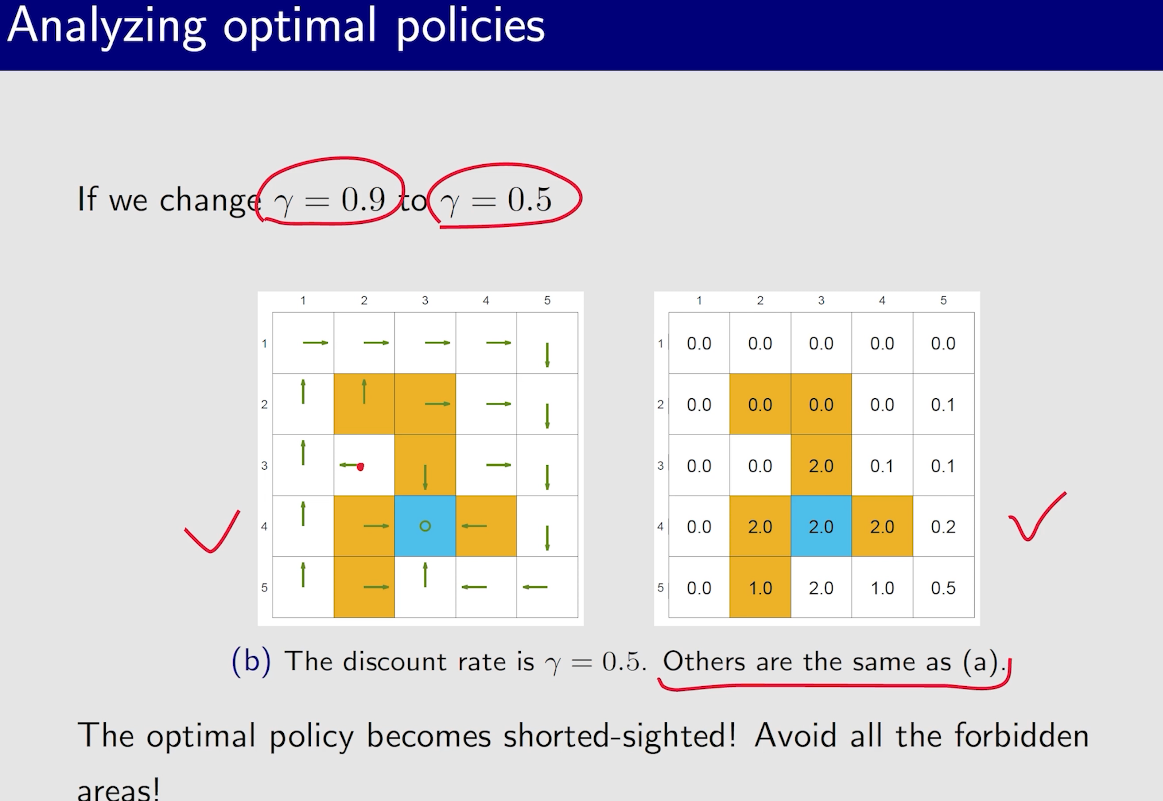
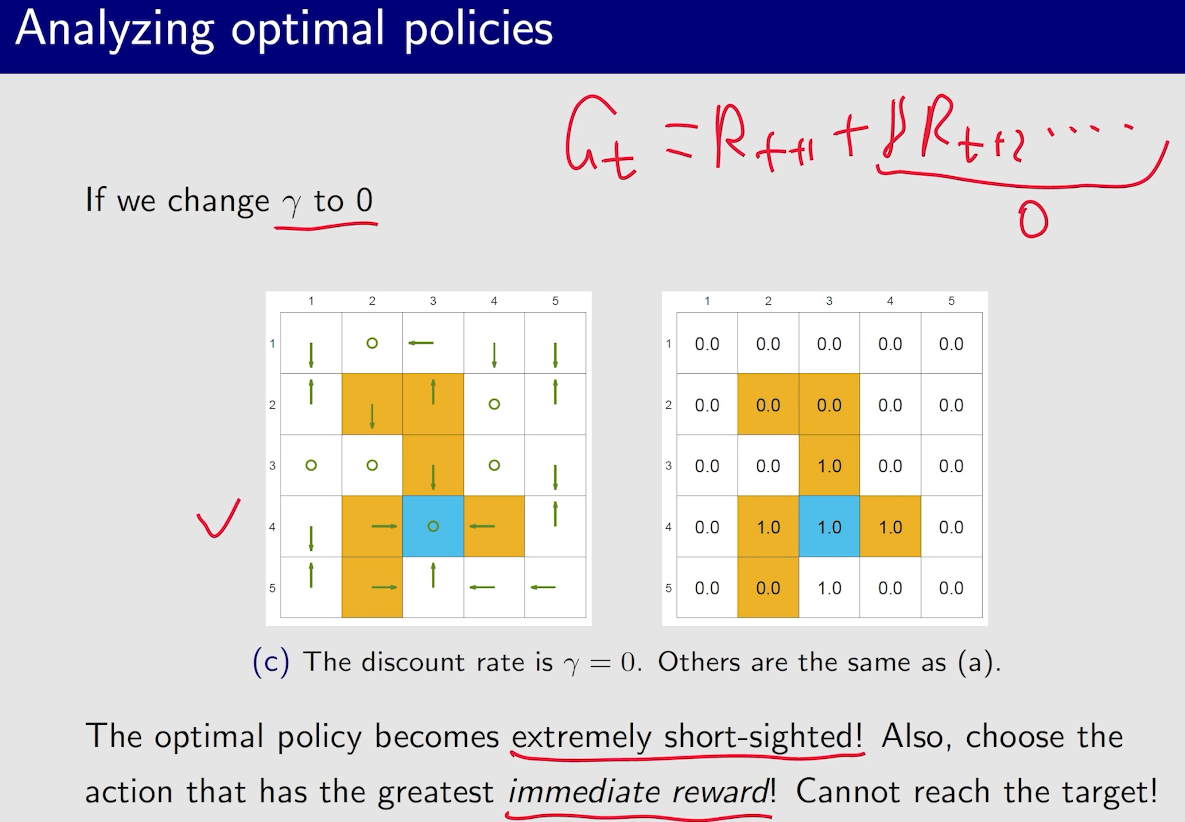
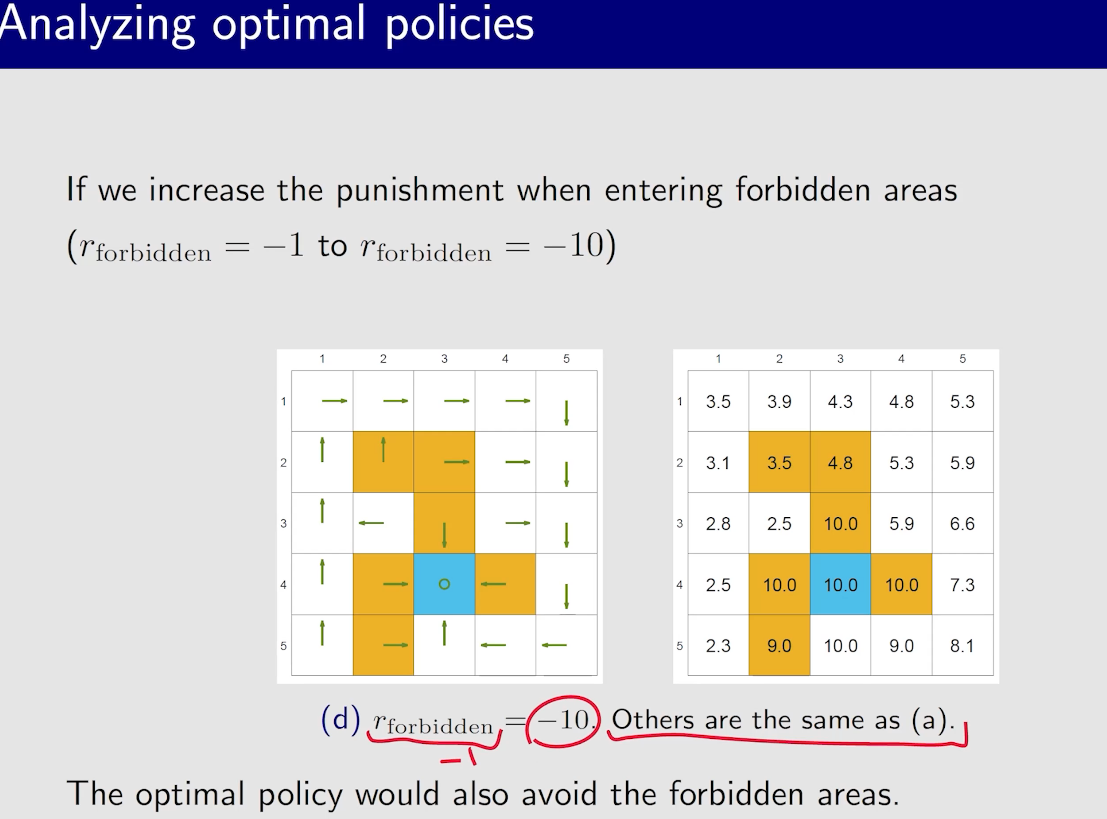
最优策略的不变性

只考虑相对价值的大小

一般为了防止绕远路，每一步会给$r=-1$，但其实，这个不止和$r$有关，和$\gamma$也有关系

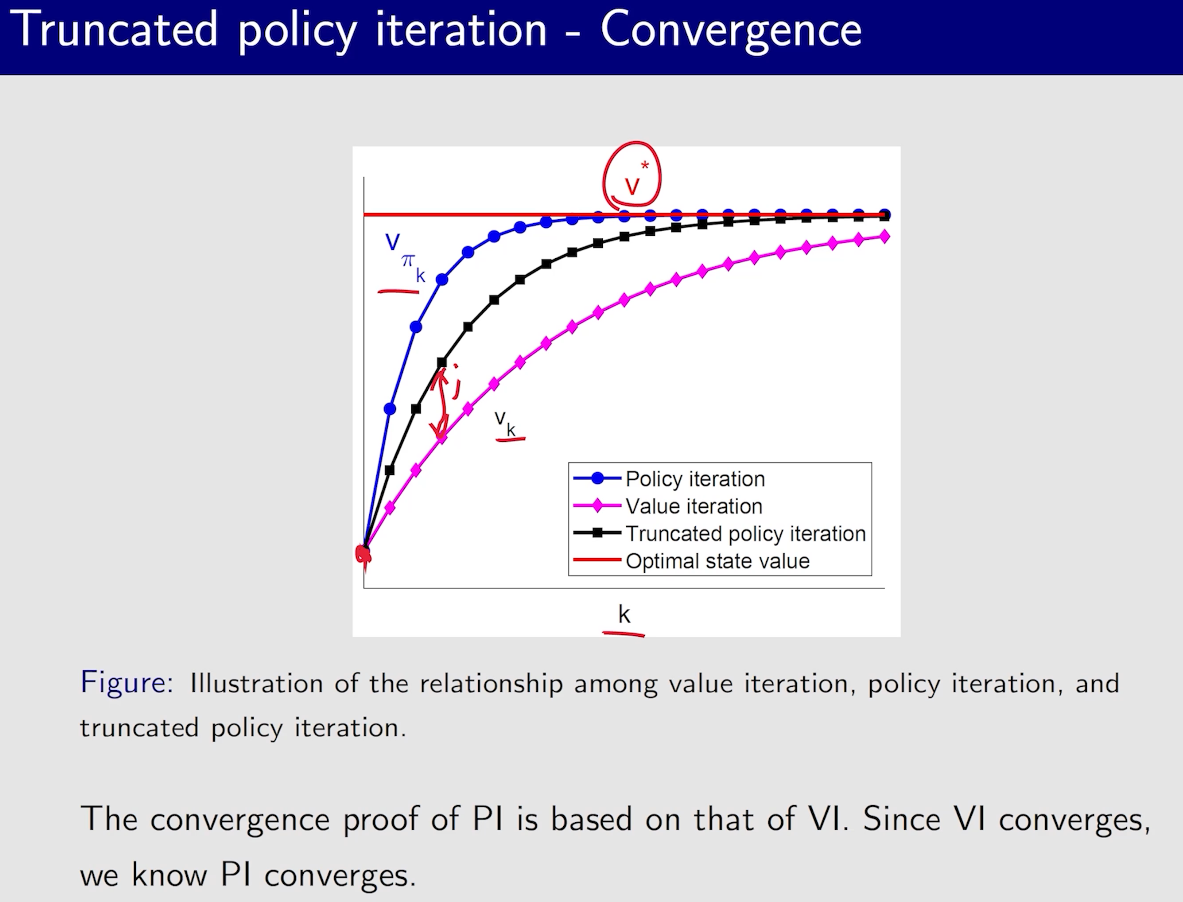
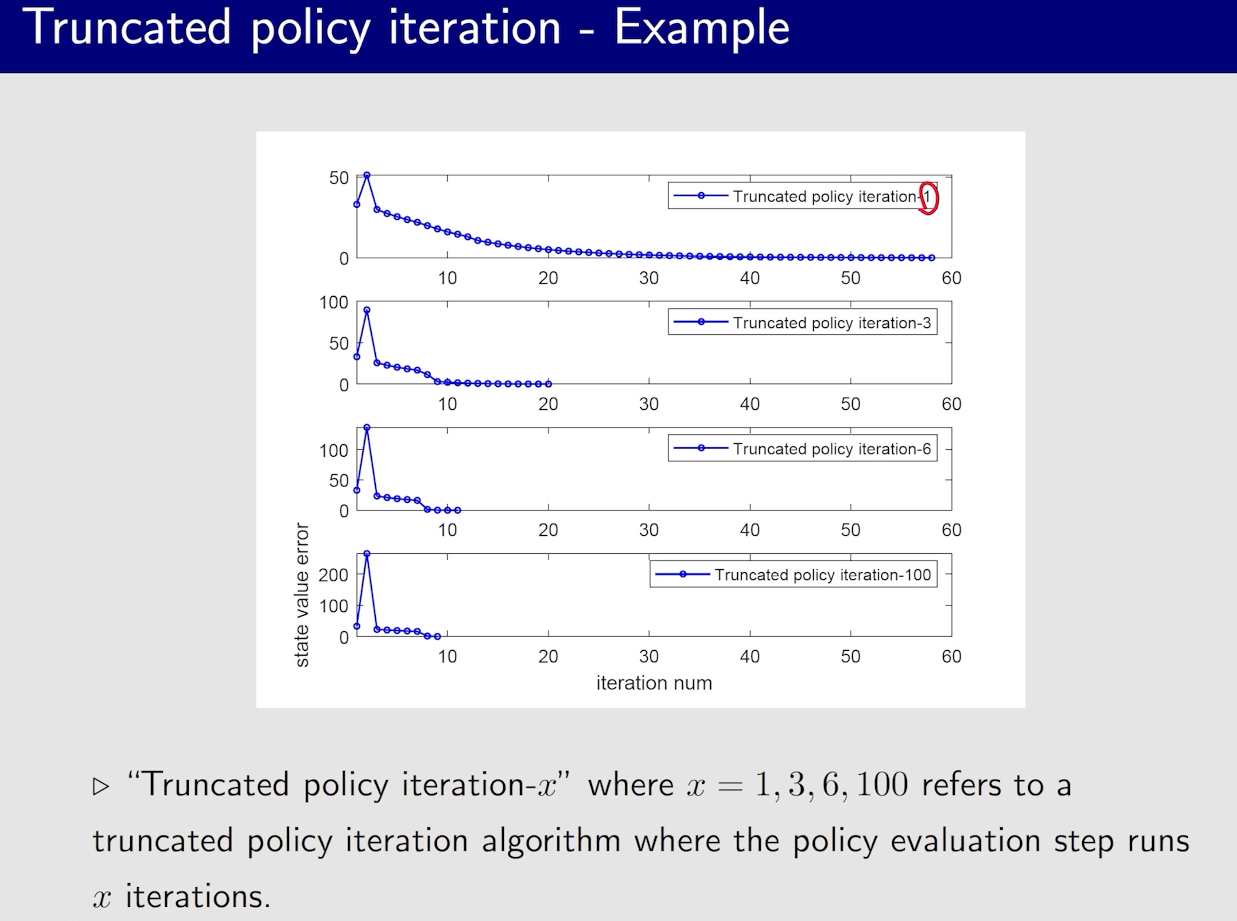
值迭代与策略迭代

有一个现象：接近目标的状态策略会先变好

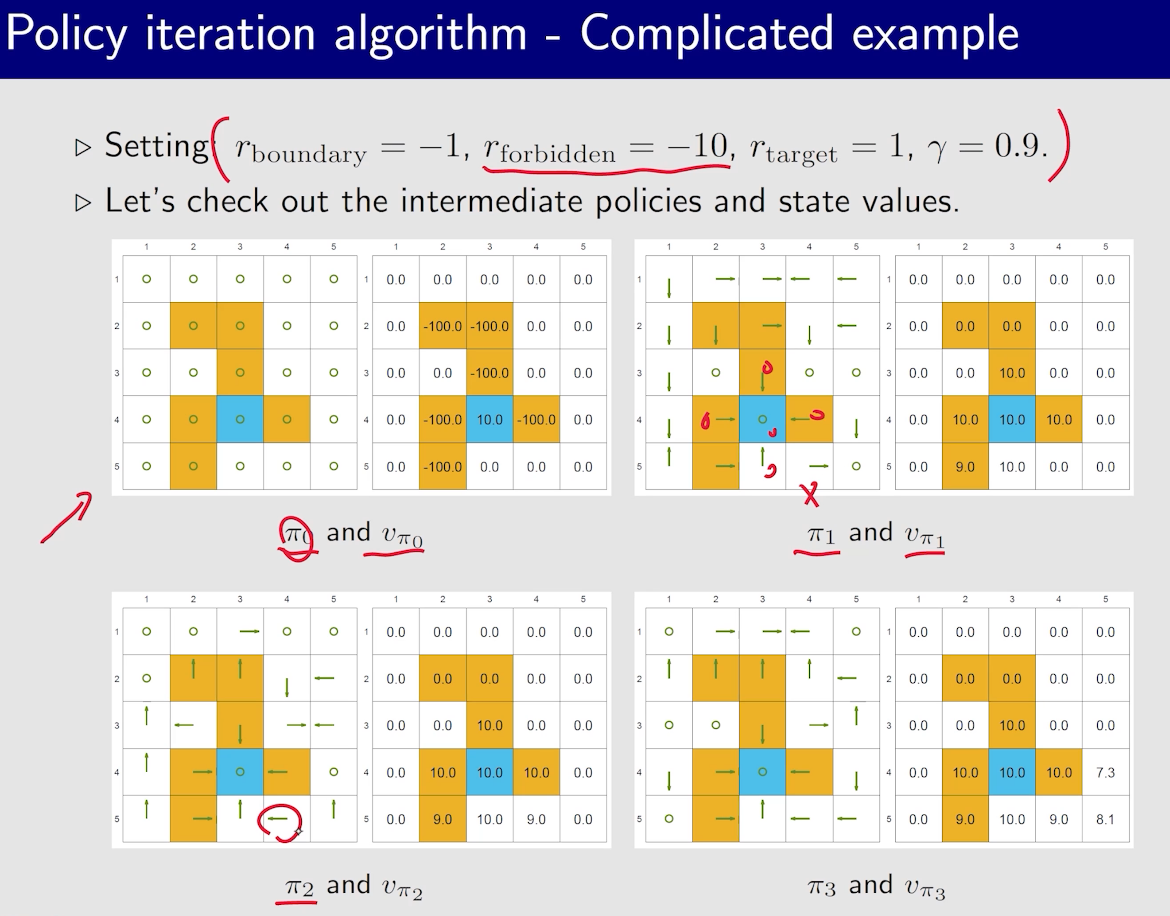
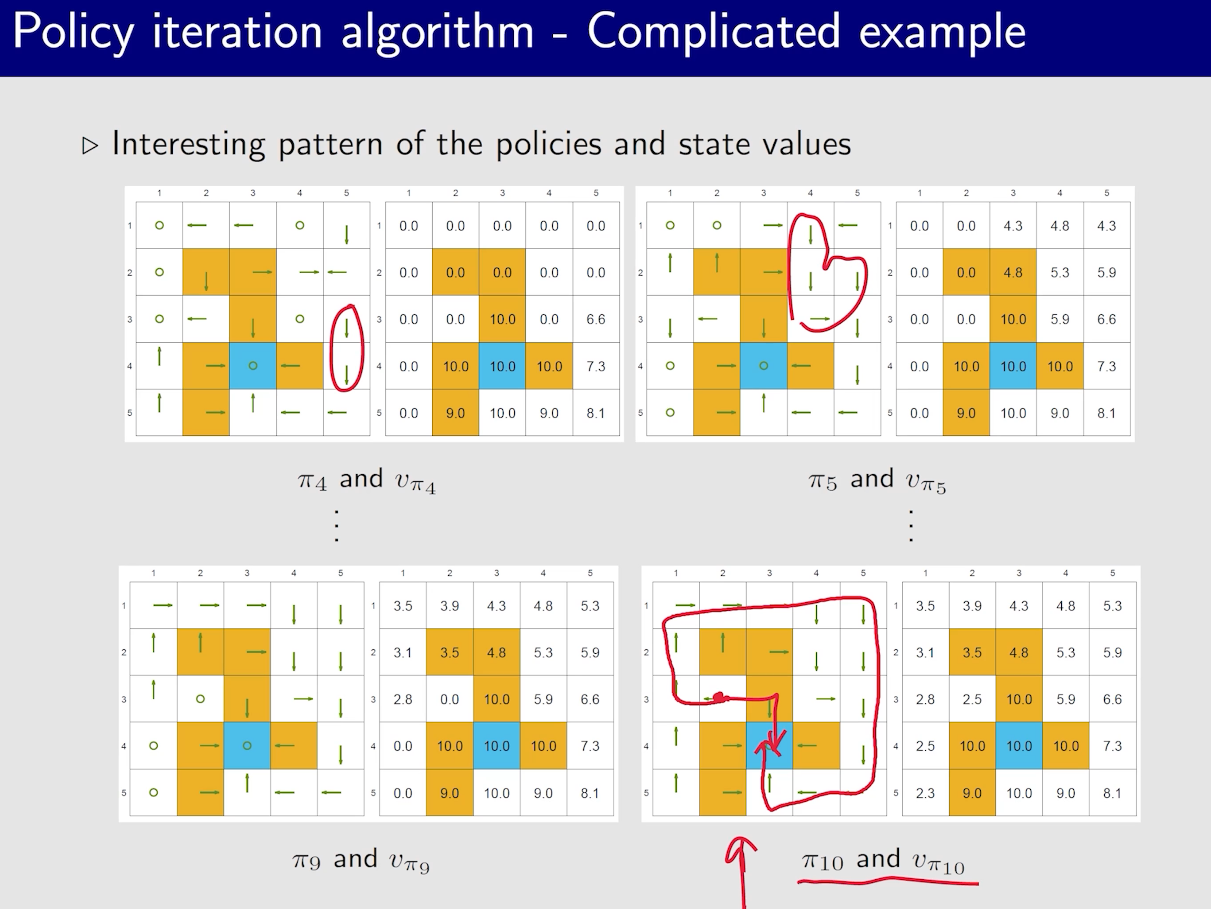
蒙特卡洛方法

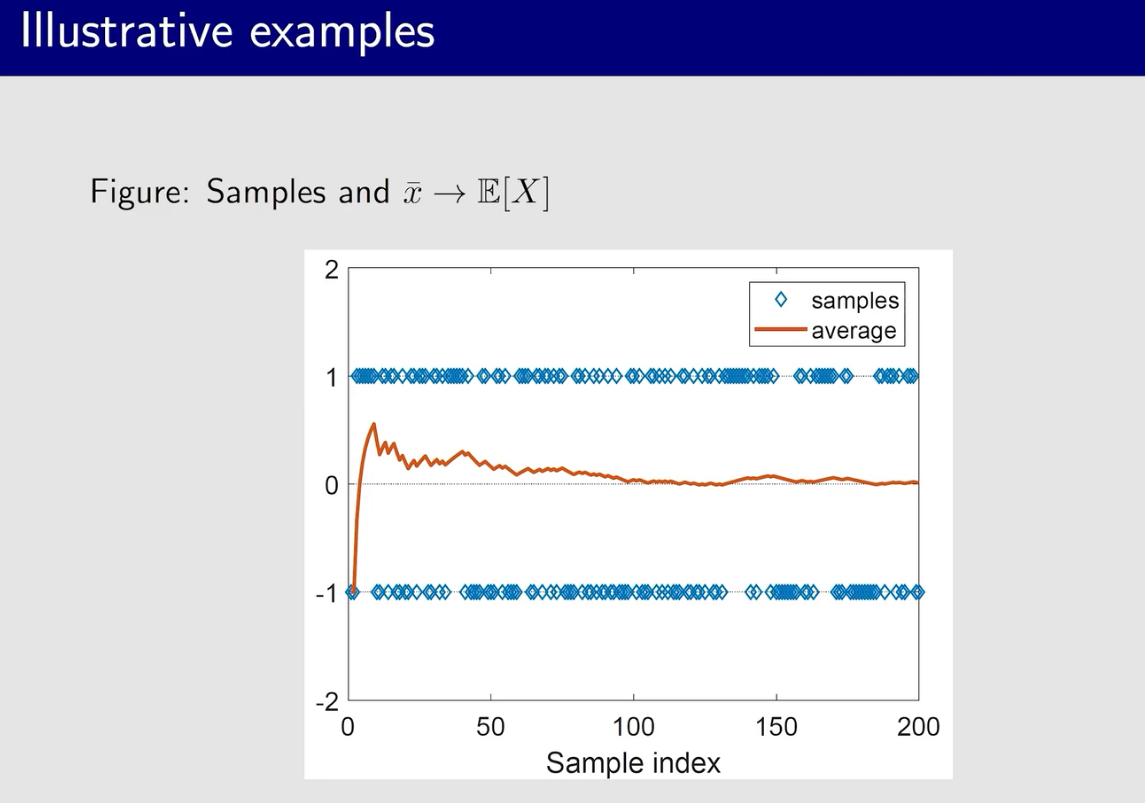
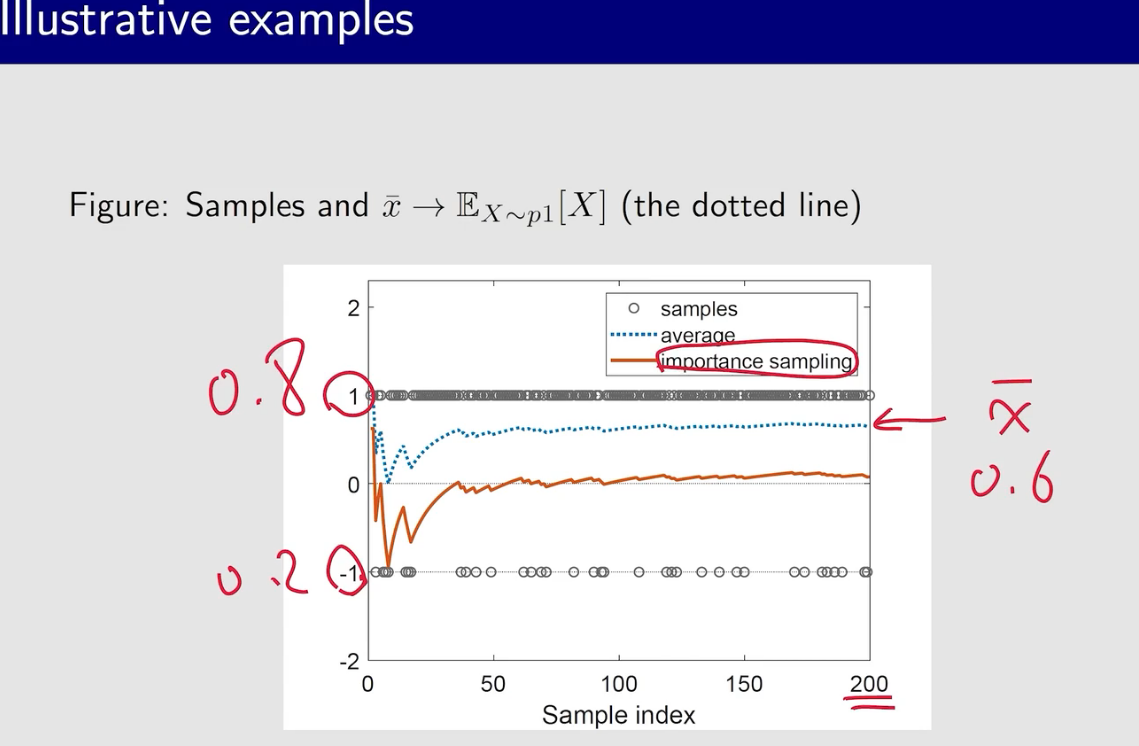
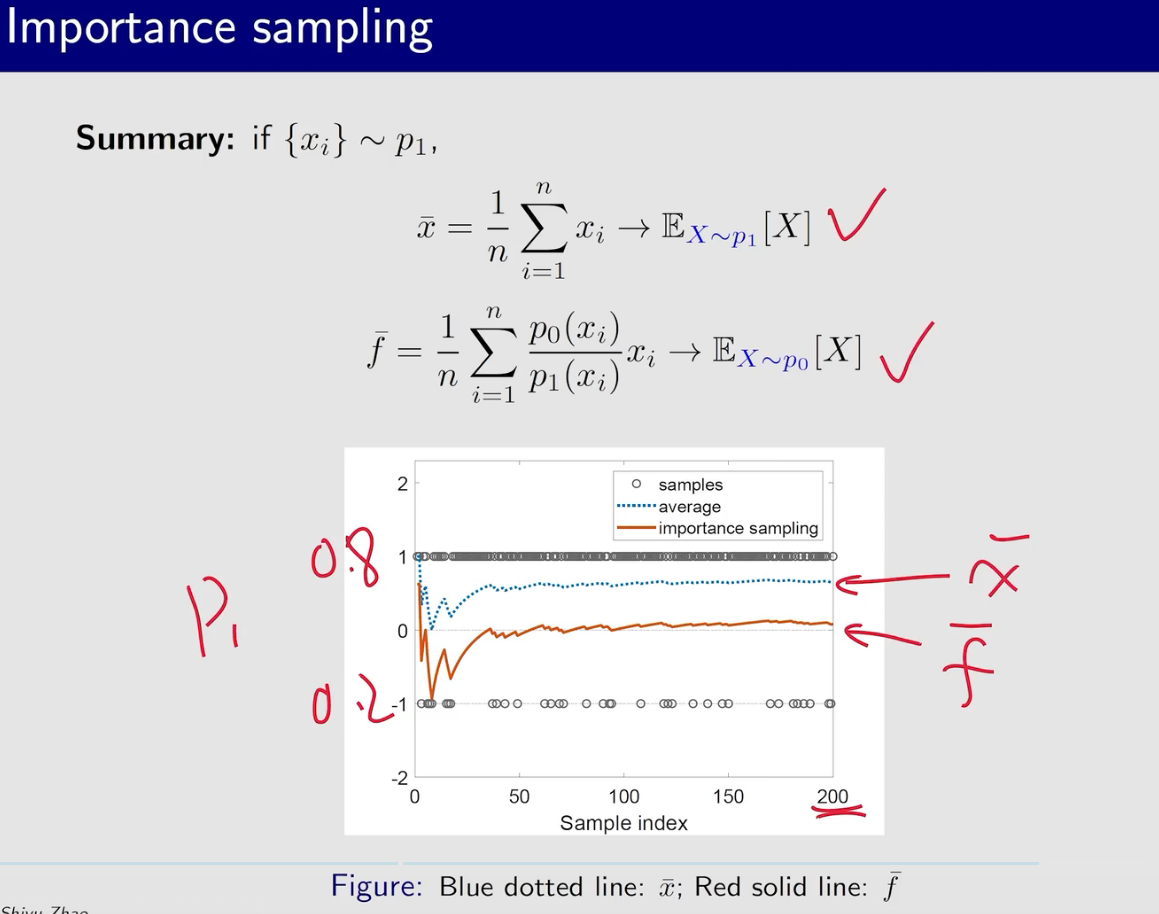
蒙特卡洛估计

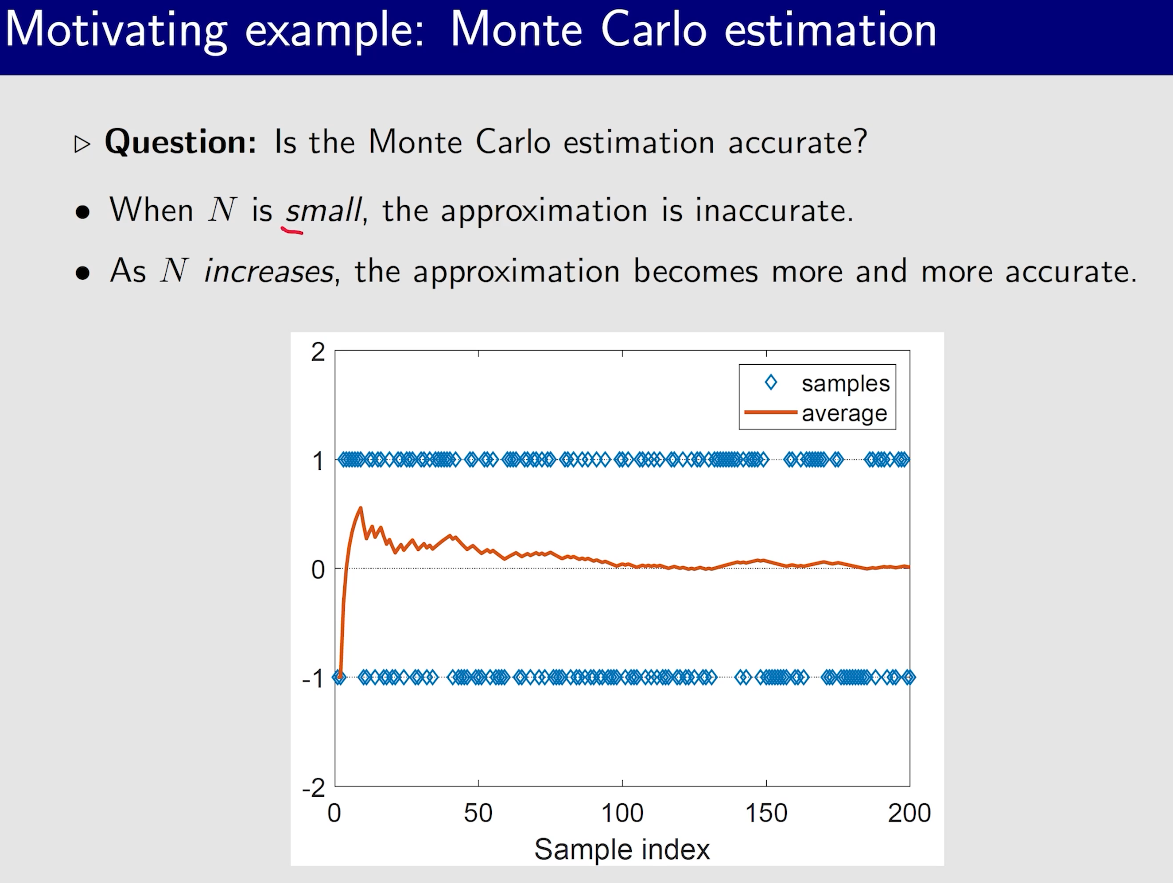
大数定律是根本保证

MC Basic

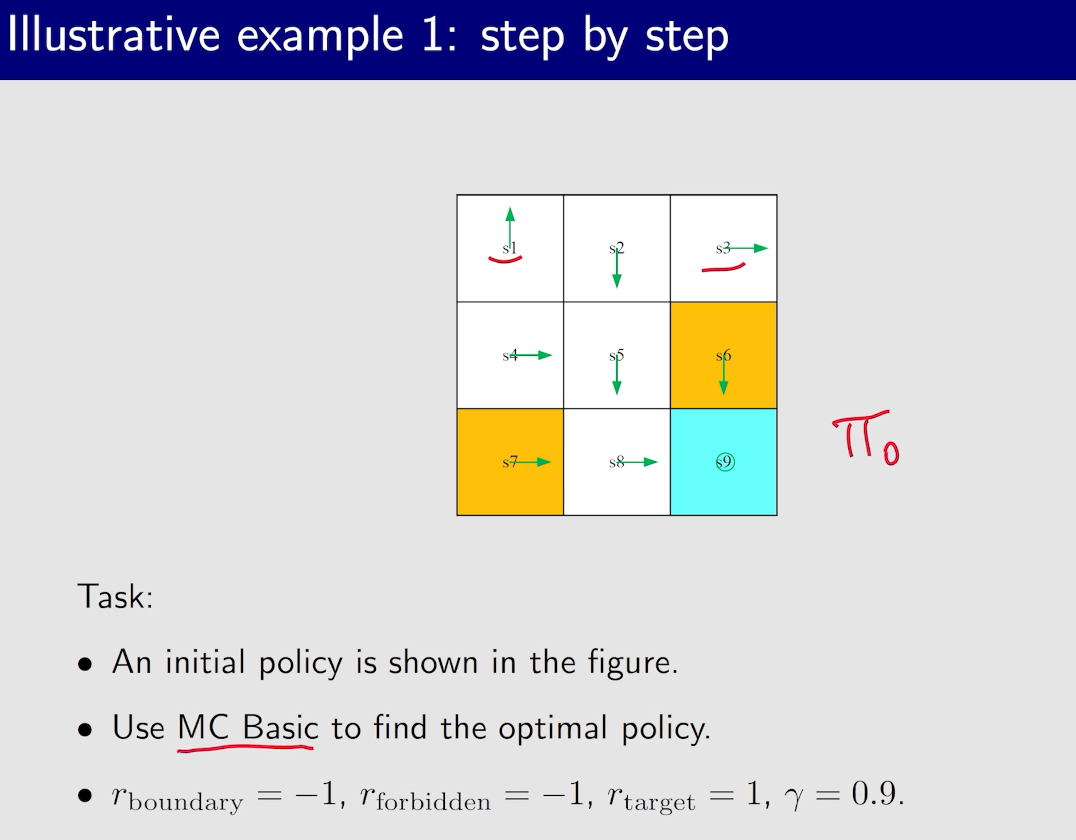
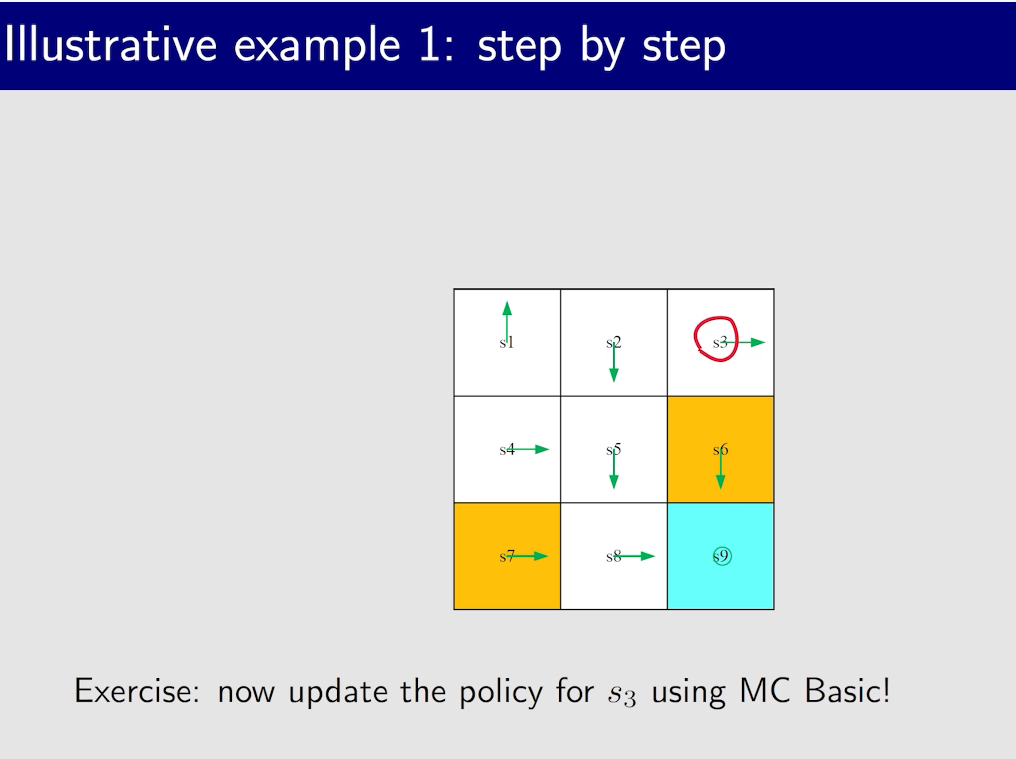
MC Exploring Starts

如果一个状态在一个序列中出现了多次，该怎么处理？这里对应两种方法，一种是只计算这个状态在序列中第一次出现的累积奖励，这种方法称为”first-visit MC method”；另一种方法是这个状态每次出现时都计算积累奖励，再取平均，称为”every-visit MC method”。

MC Epsilon-Greedy

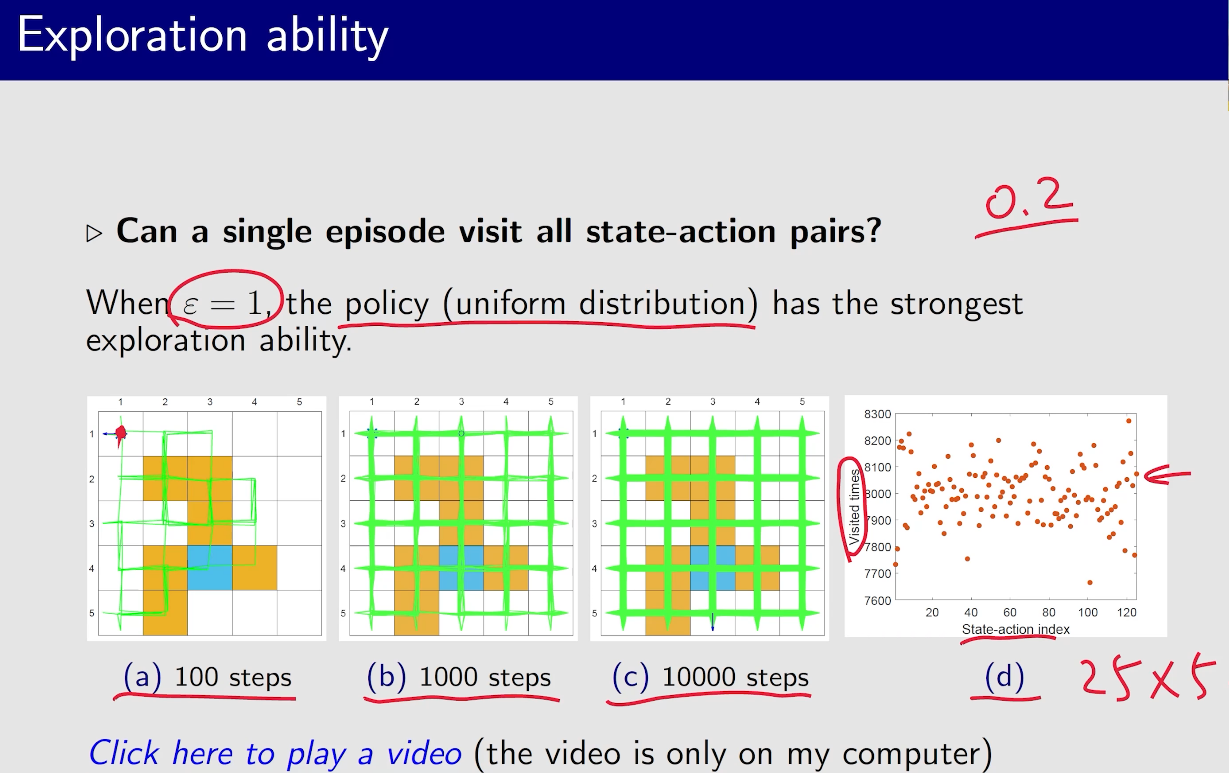
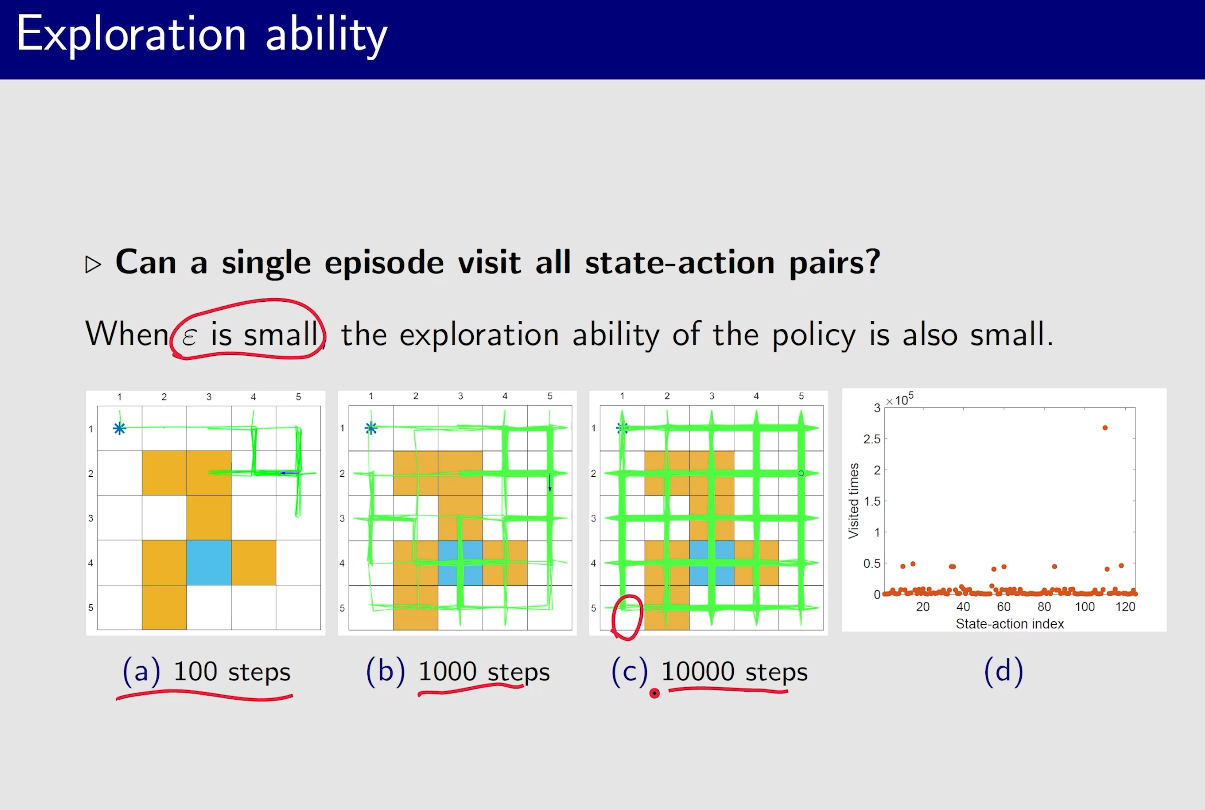
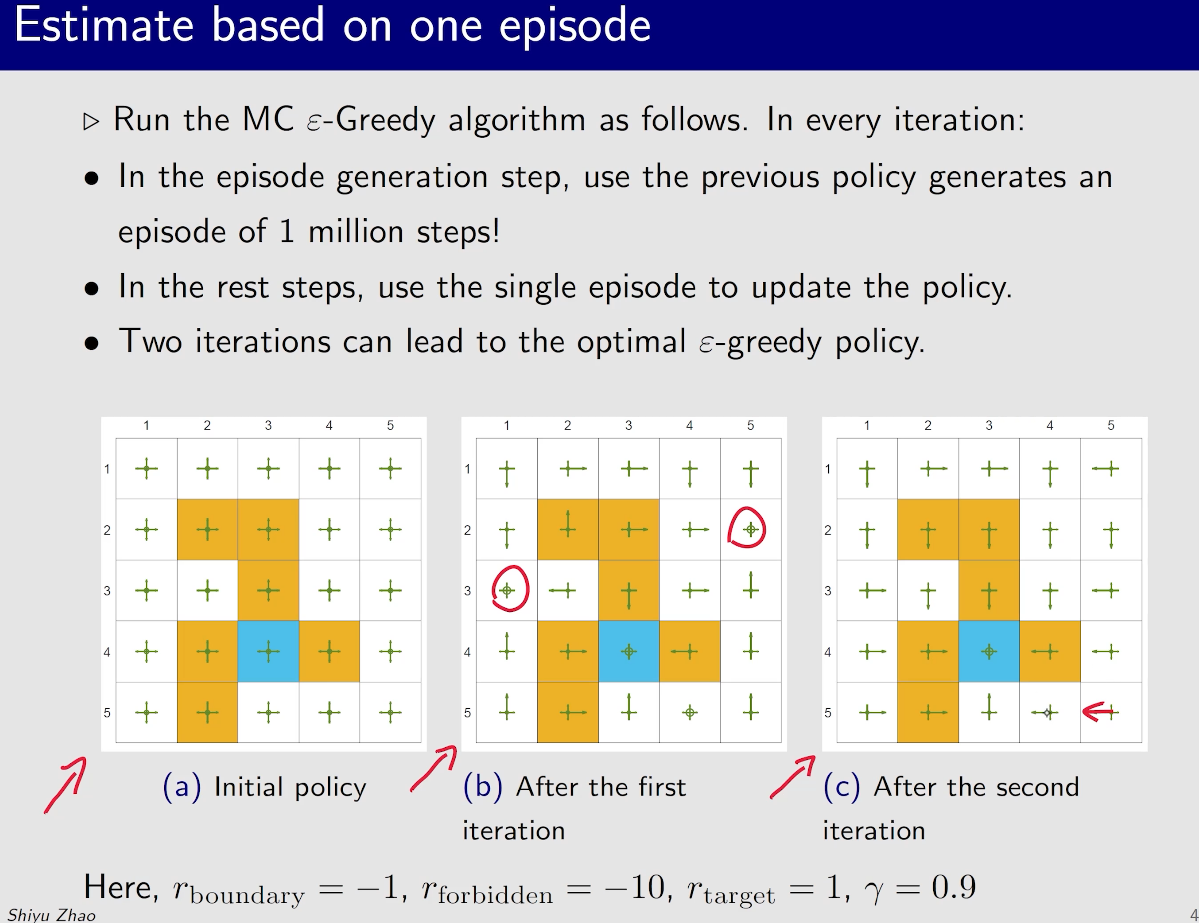
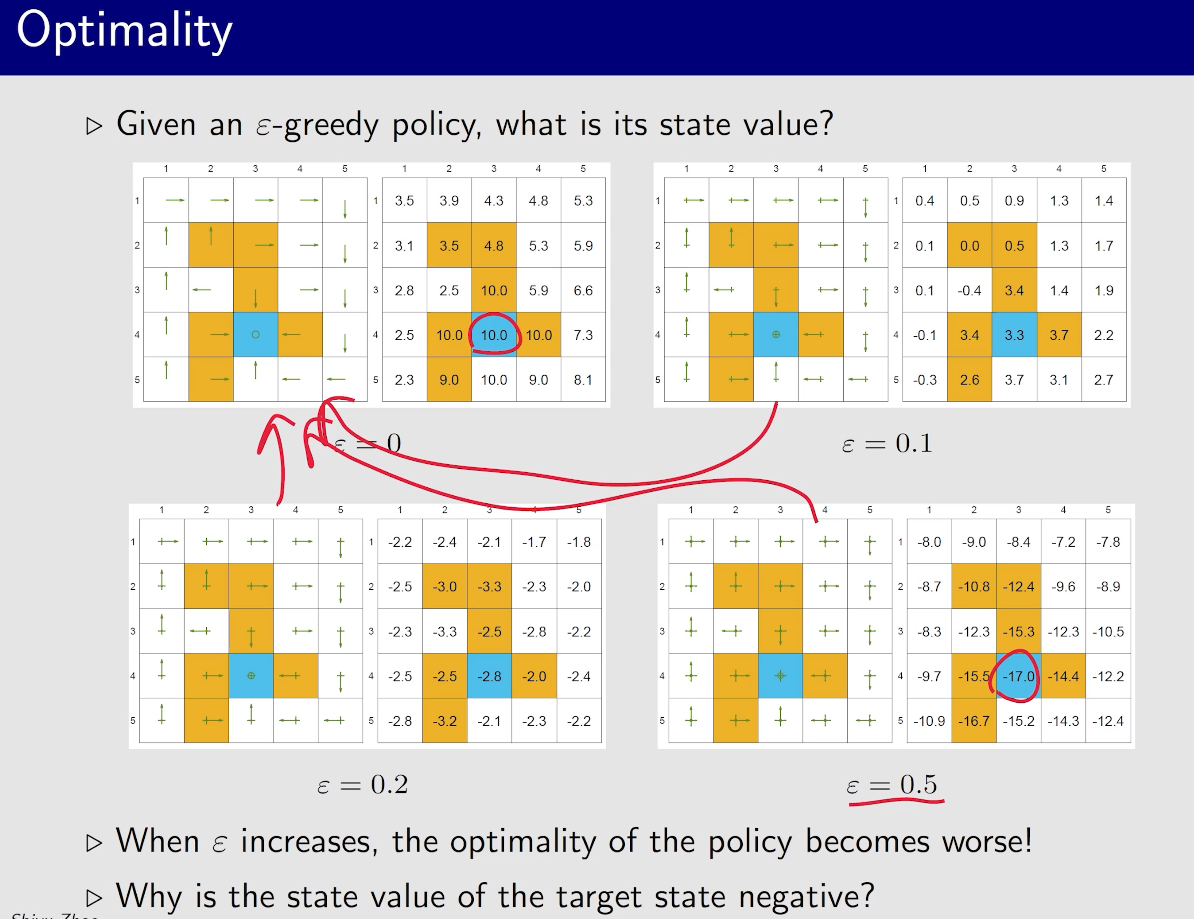
一开始$\epsilon$比较大，探索性比较强，然后$\epsilon$ 逐渐减小，到结束时$\epsilon=0$,这是就能得到一个比较优的策略

随机近似与随机梯度下降

SA

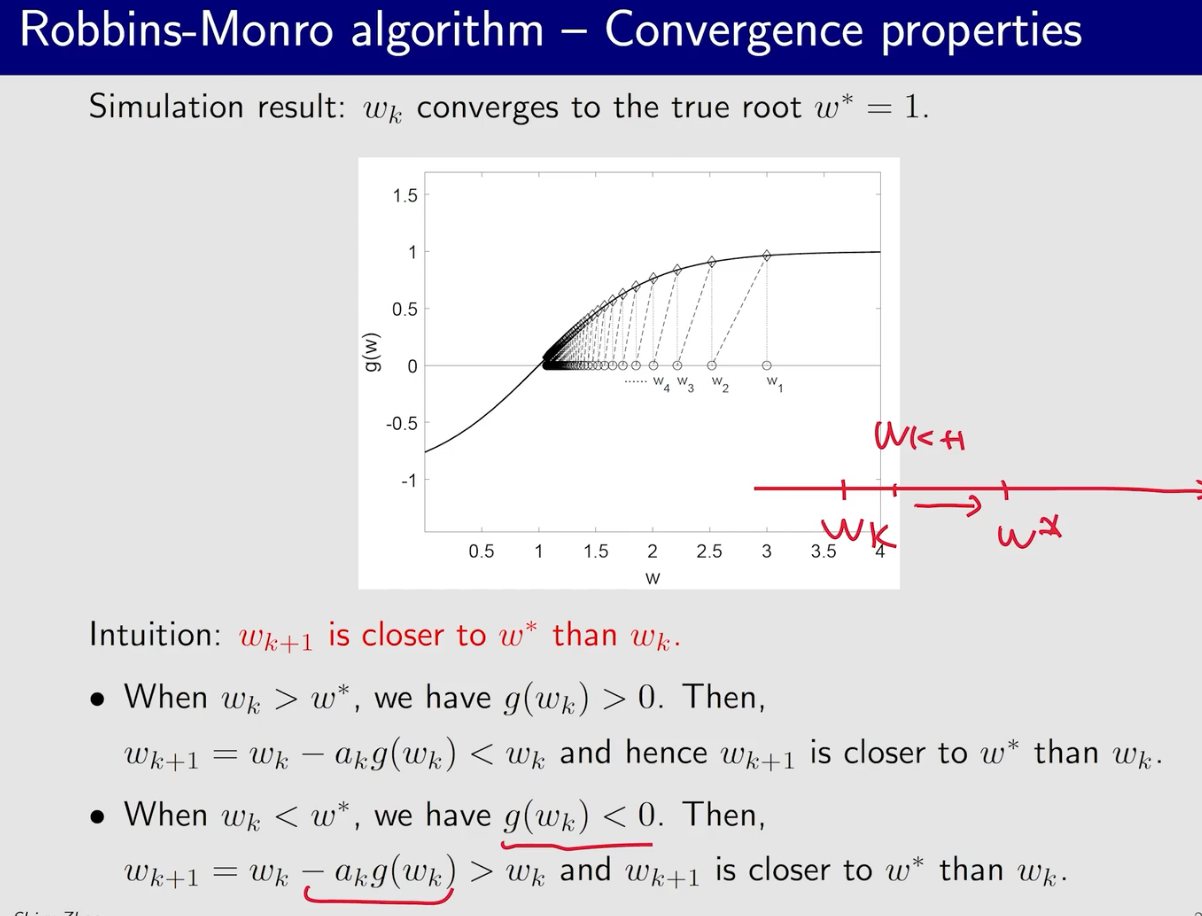
练习：求解$(x-1)^2-1=0$

int main(){
    auto g = [=](double x) -> double{return (x-1)*(x-1)-1;};
    double w = 8,a = 100;
    for (int i = 1;i <= 1000;++ i){
        double w_t = w;
        w = w_t - (1./a)*g(w_t);
        printf("%.4lf\n",w);
        // a += 1;
    }

}

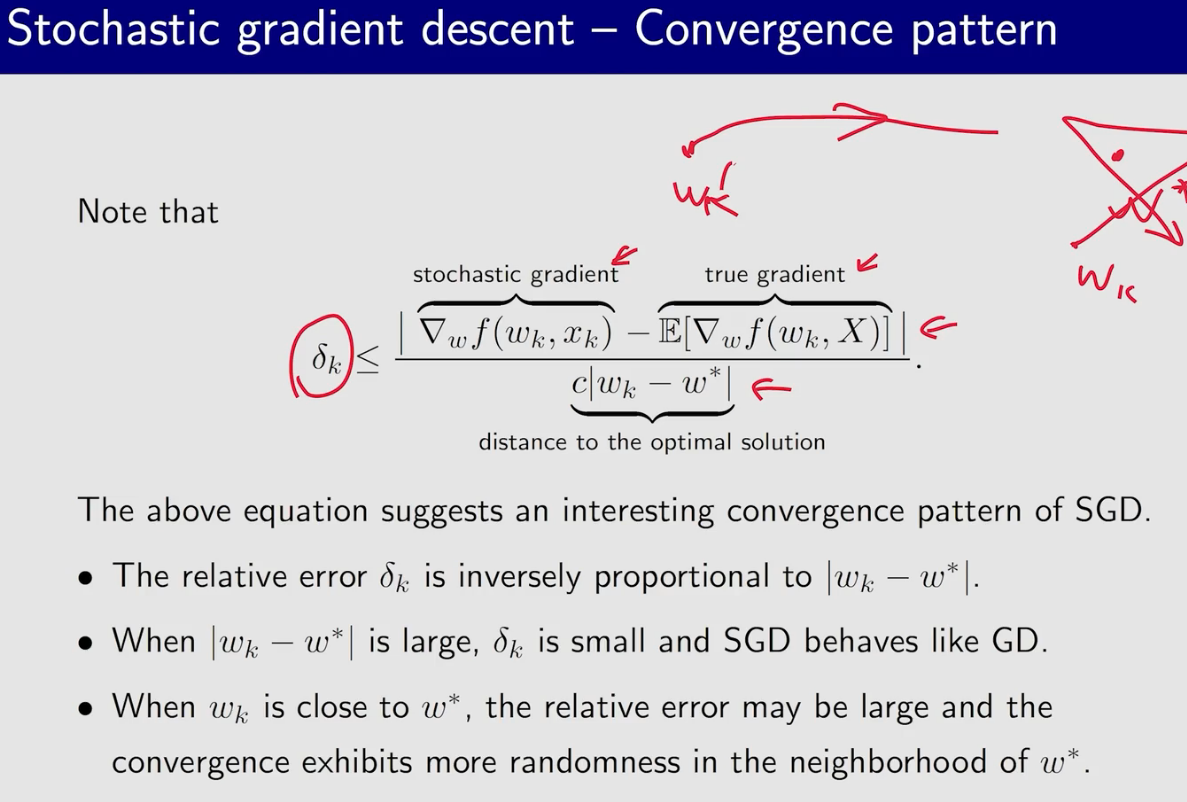
SGD

当$w_k和w^*$比较远的时候，sgd基本等同于gd；而比较近的时候sgd呈现出较大的随机性误差

时序差分方法

TD to estimate state value

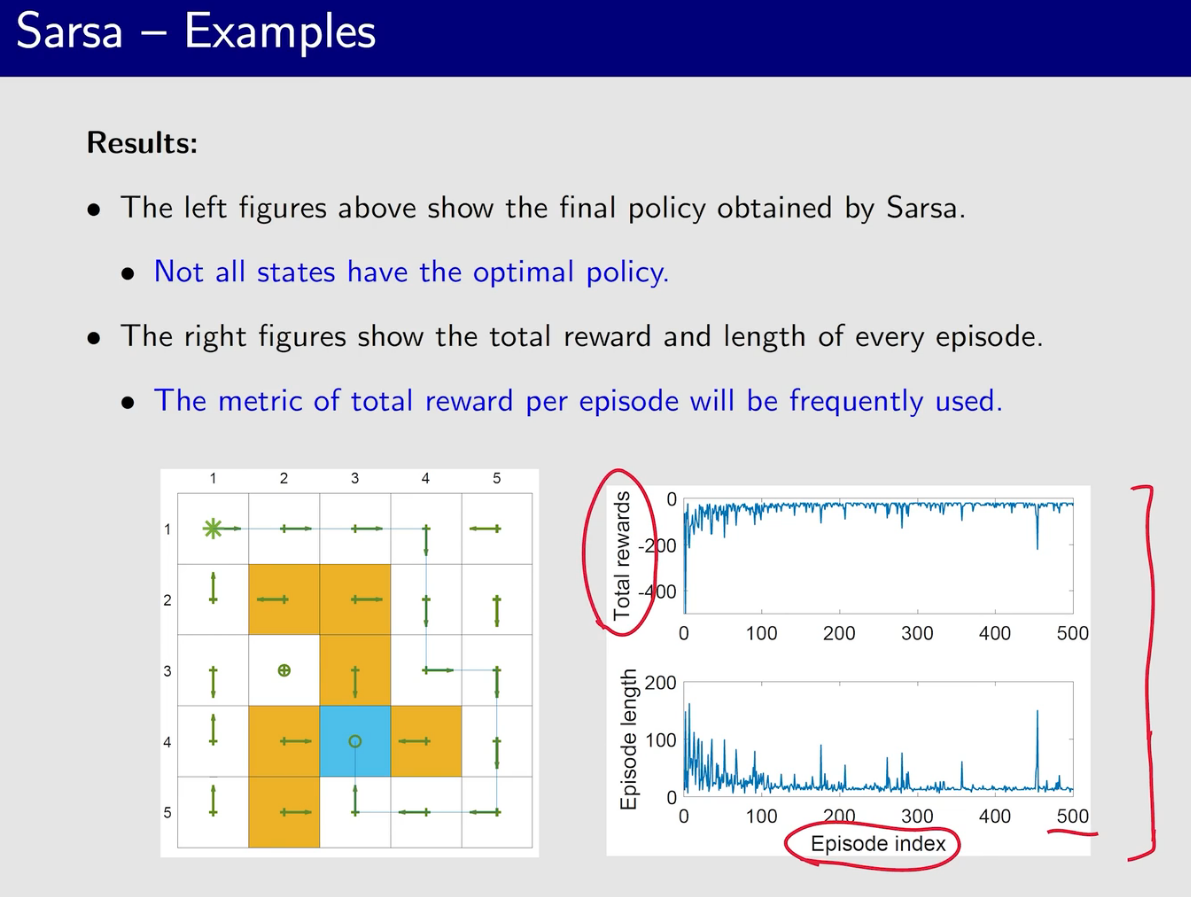
Sarsa

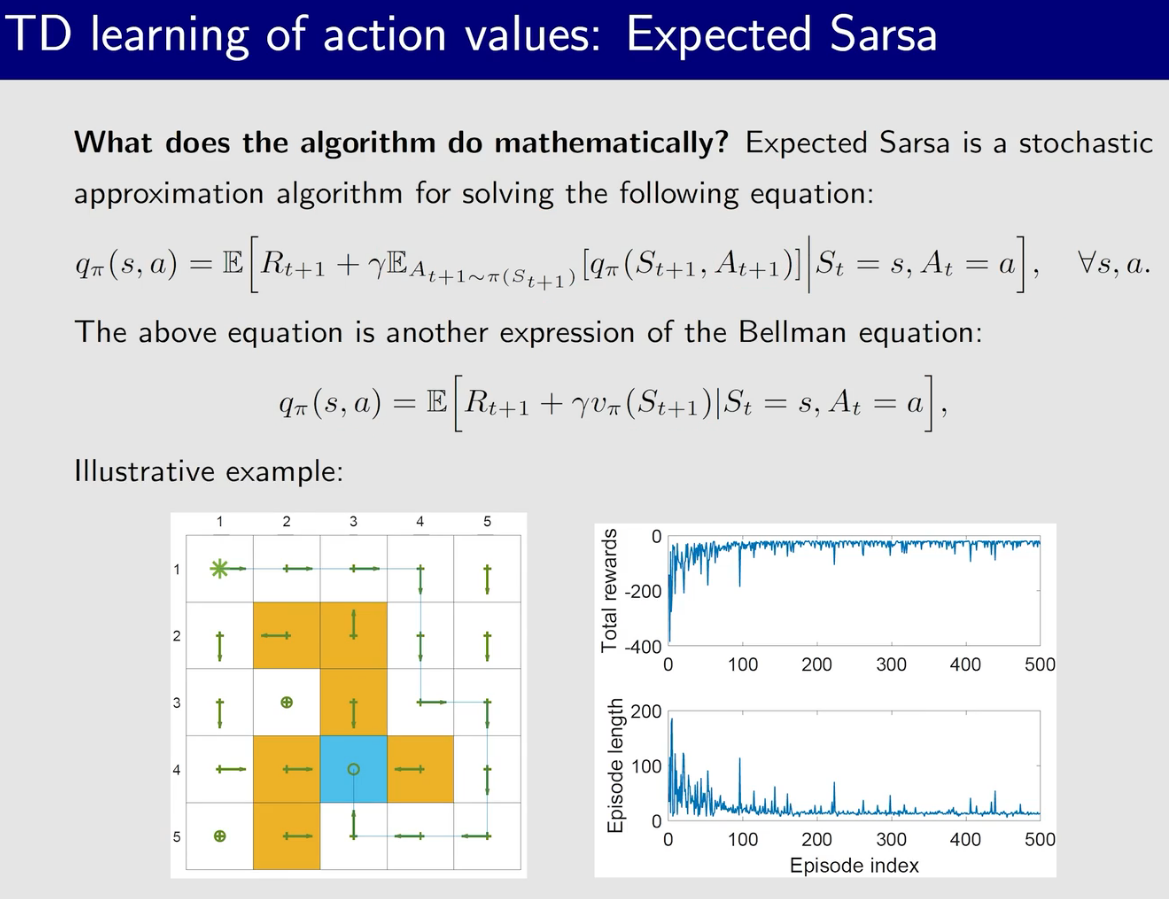
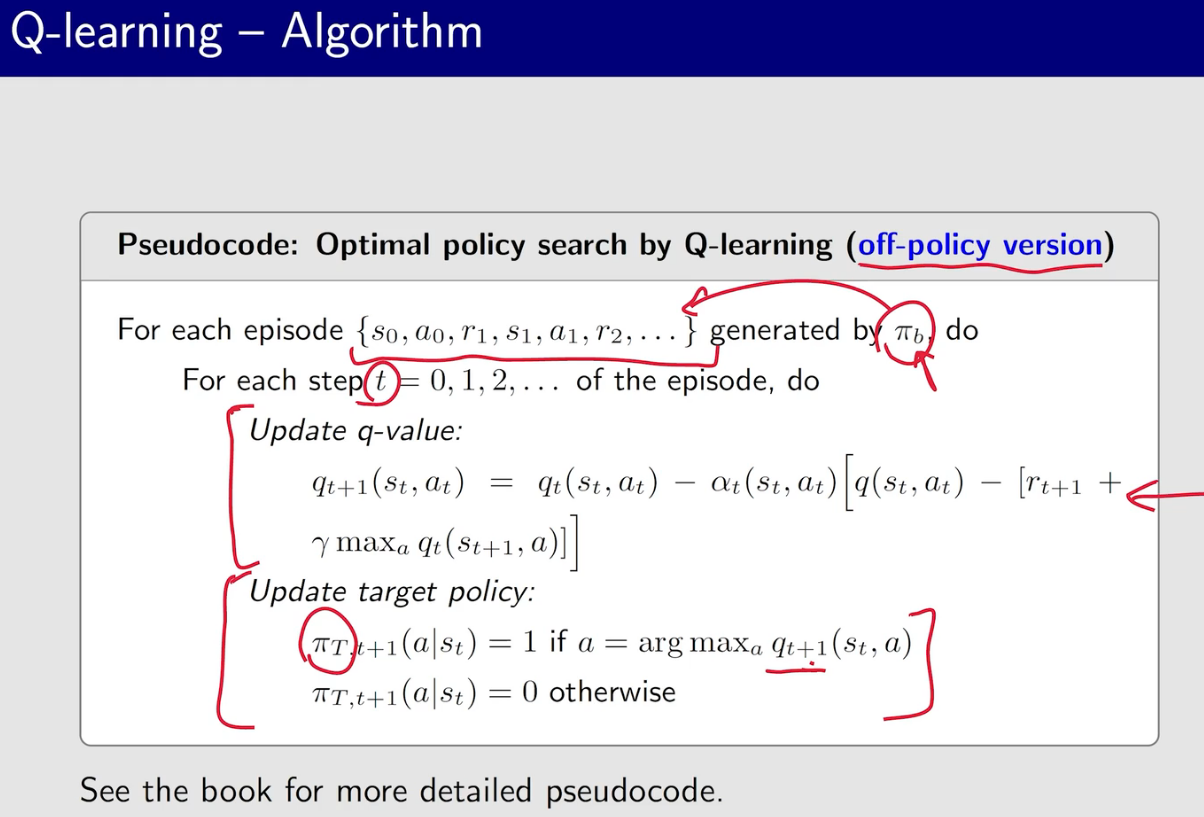
Q-learning

q-learning 的behavior policy 和 target policy可以相同也可以不同

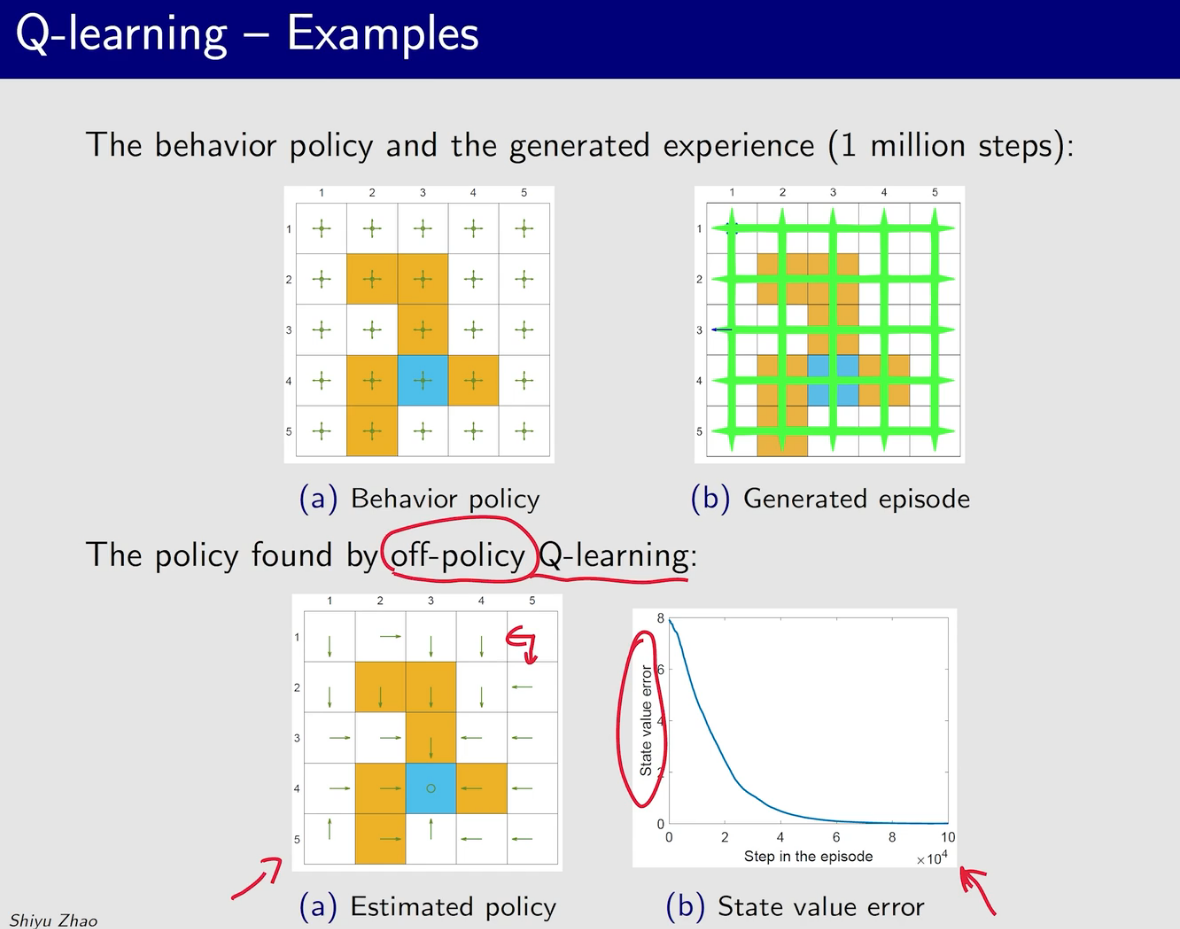
一开始的探索性应该比较强，然后逐渐减小

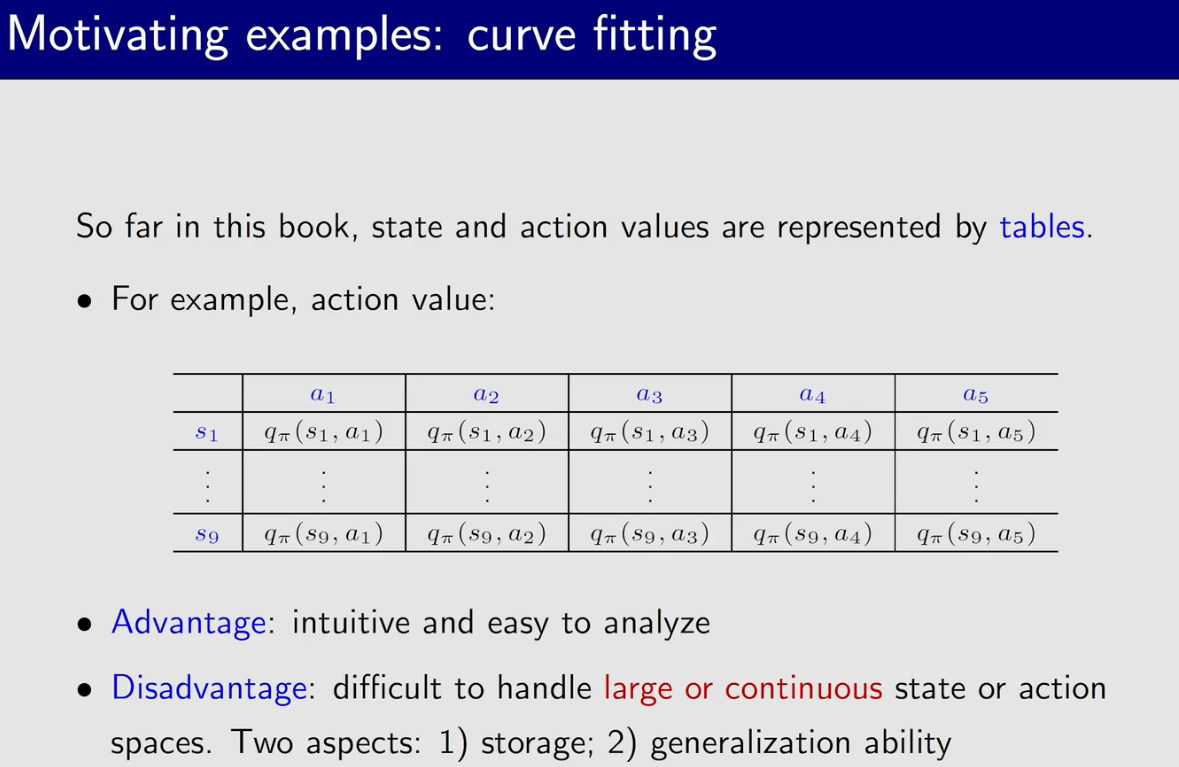
值函数近似(value function approximation)

开始的时候波动还比较大，随着访问次数的增多，曲线趋于平稳。曲线最后的星号代表着理论值，也就是说我们不通过运行很多次来找到$d_{\pi}$

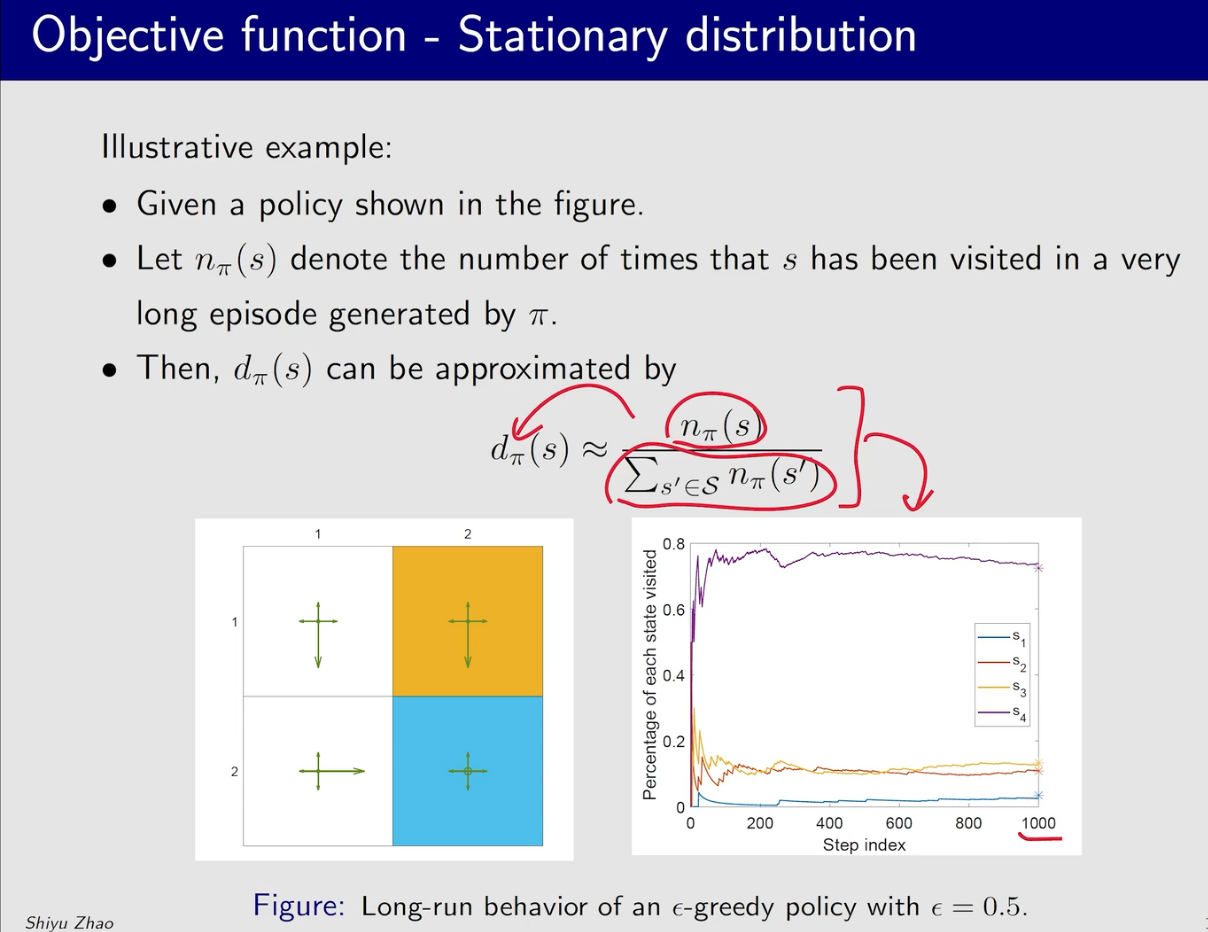
$P_{\pi}$是状态转移矩阵，$d_{\pi}$是$P_{\pi}$特征值为1的特征向量

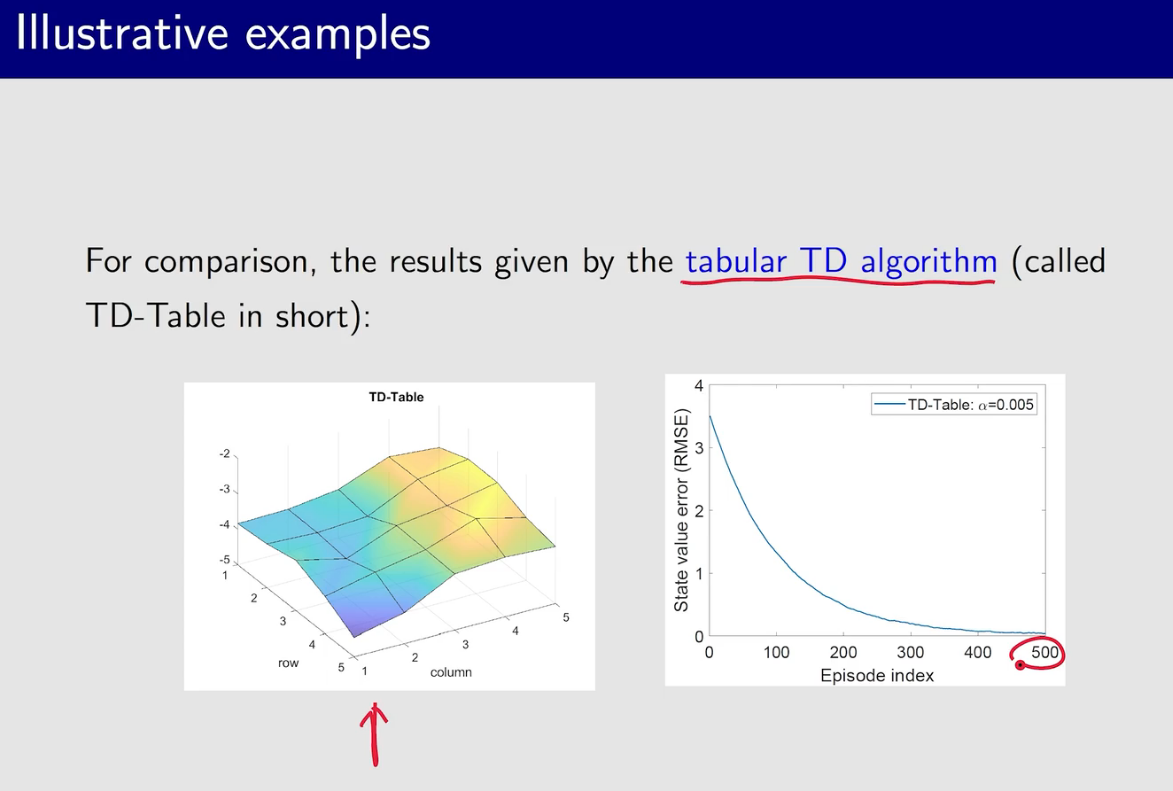
feature vector 中变量的顺序是可以调整的

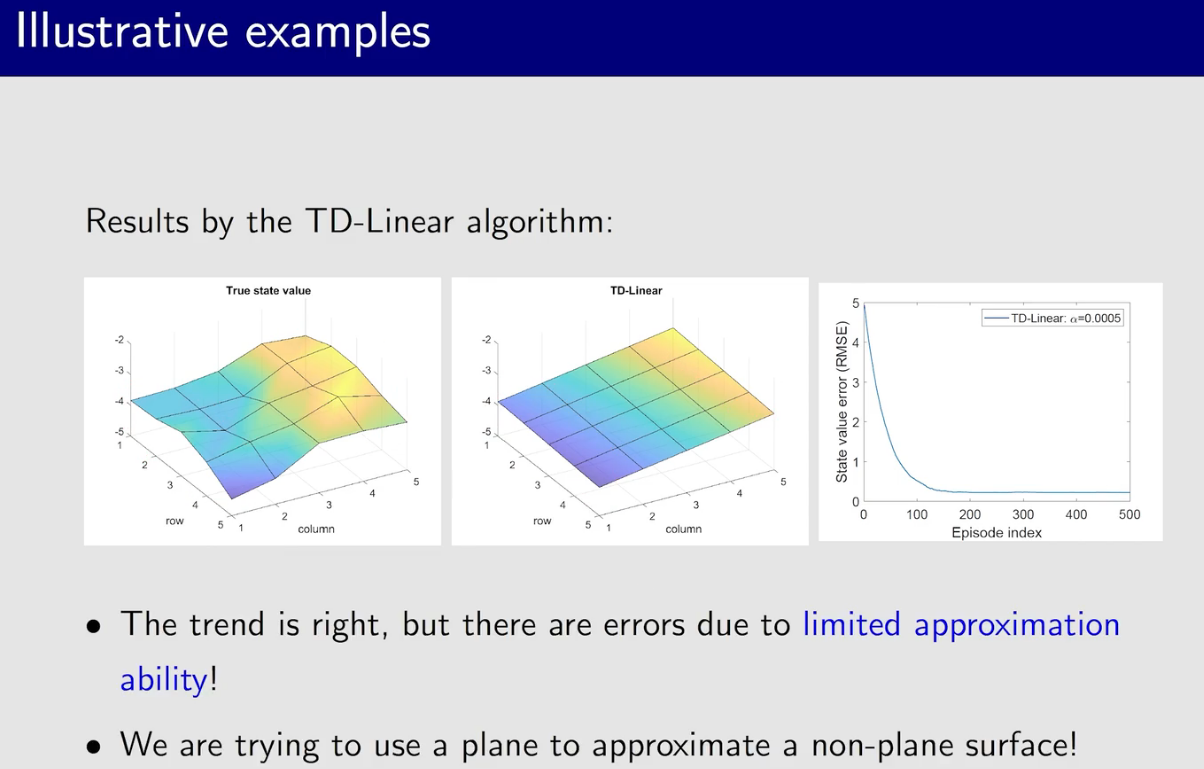
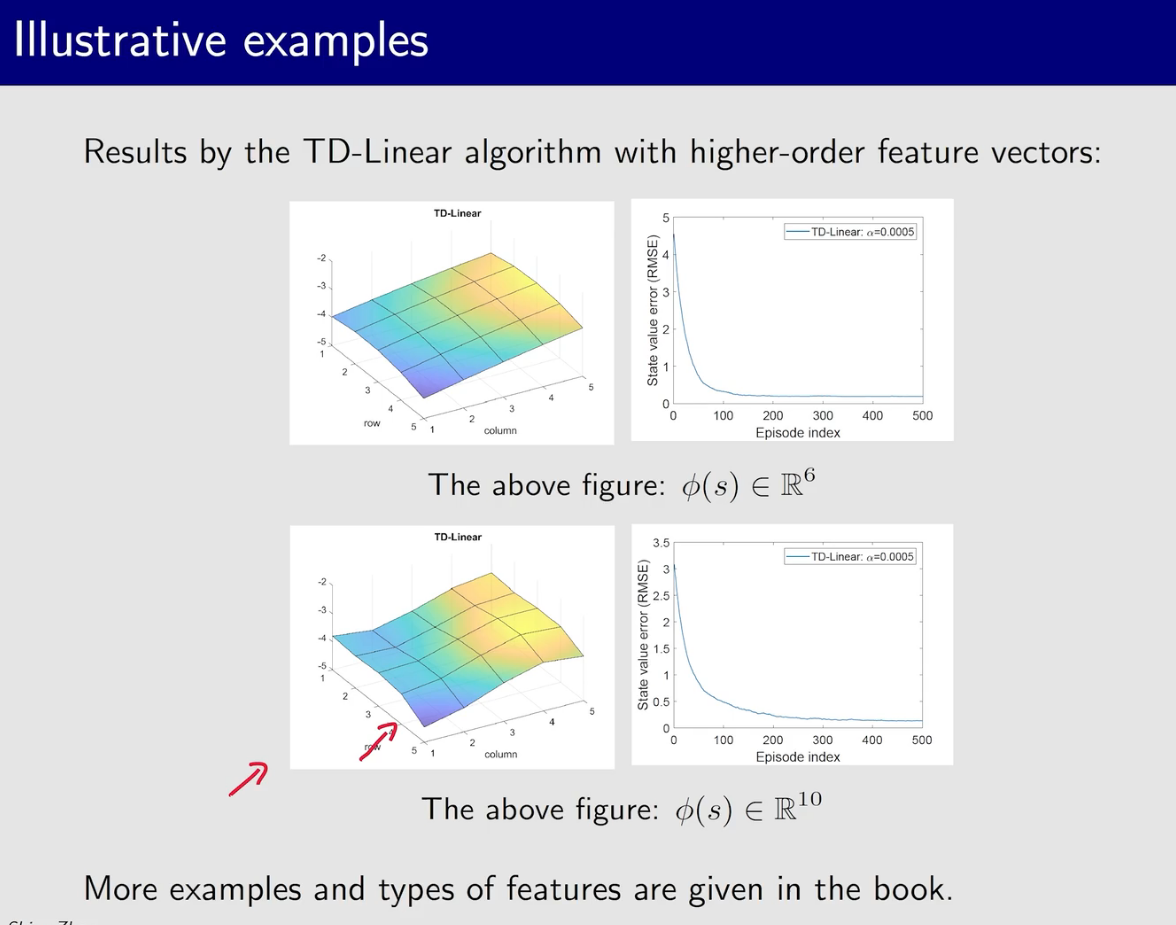
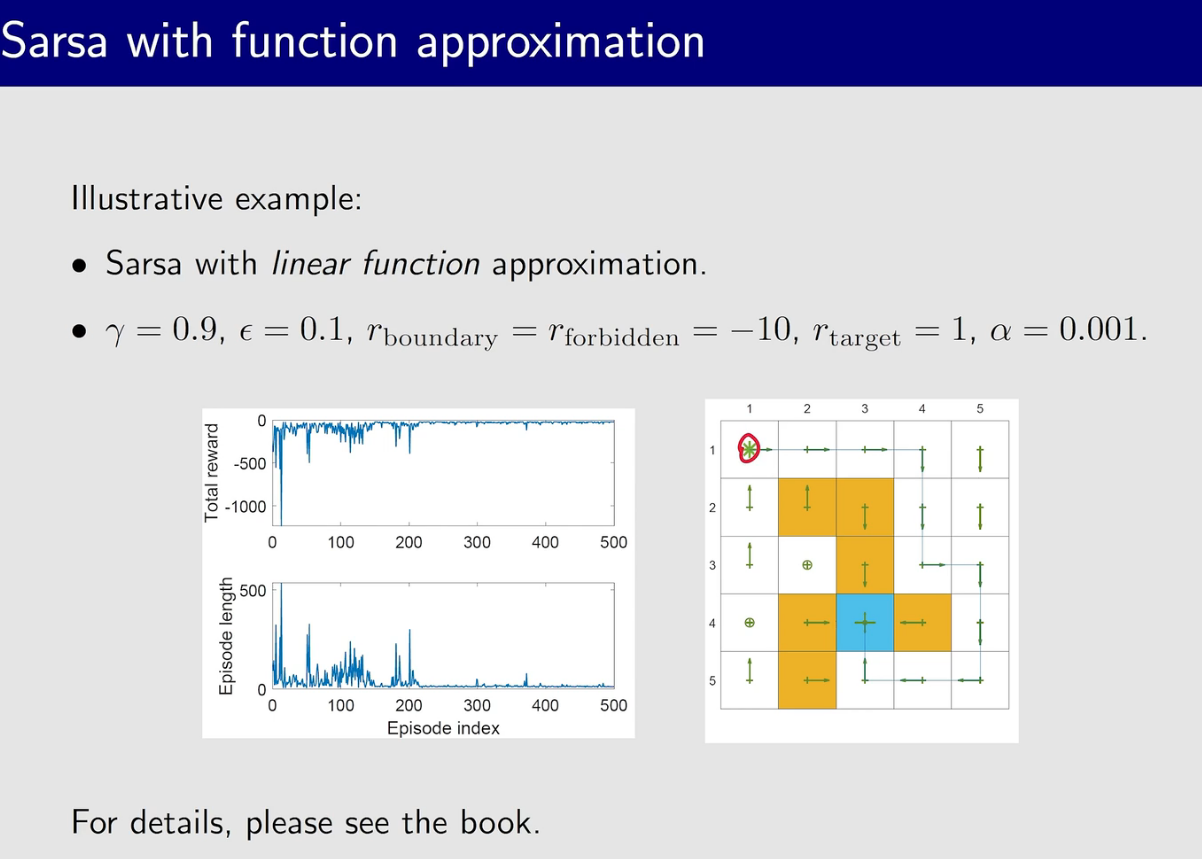
相比之前的Sarsa，这里value update 是更新的parameter $w$

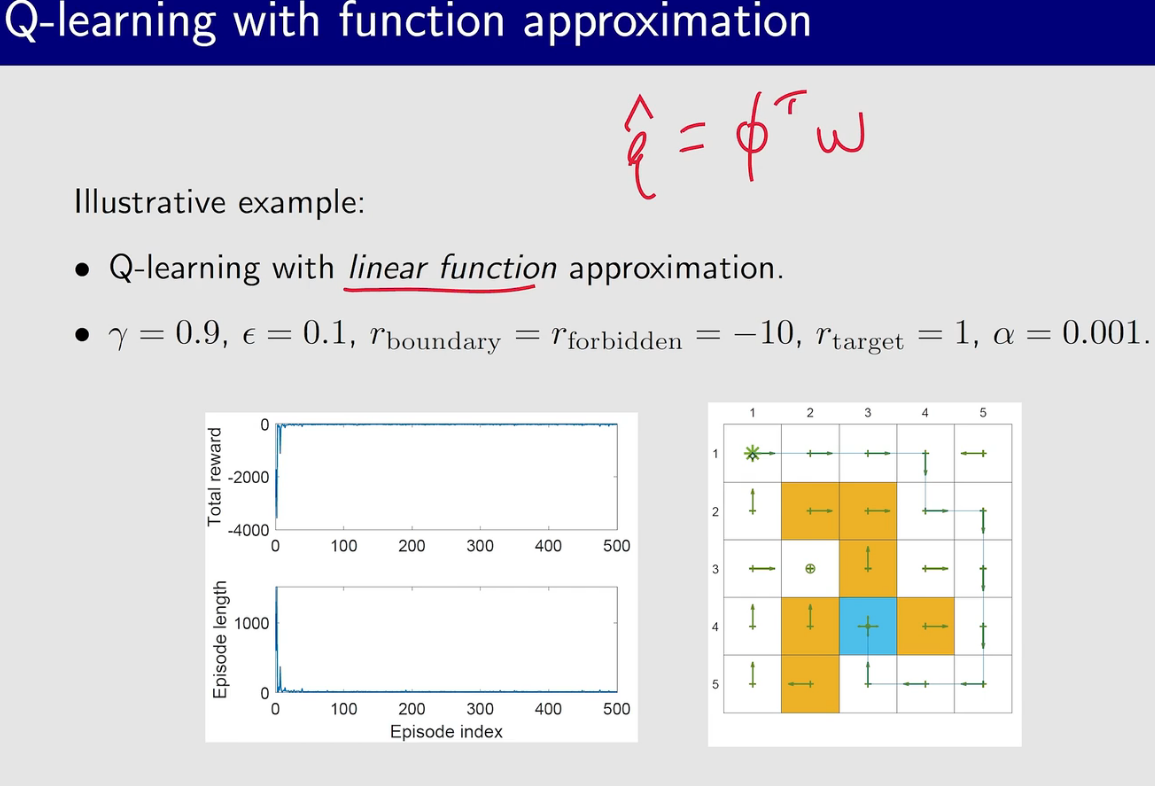
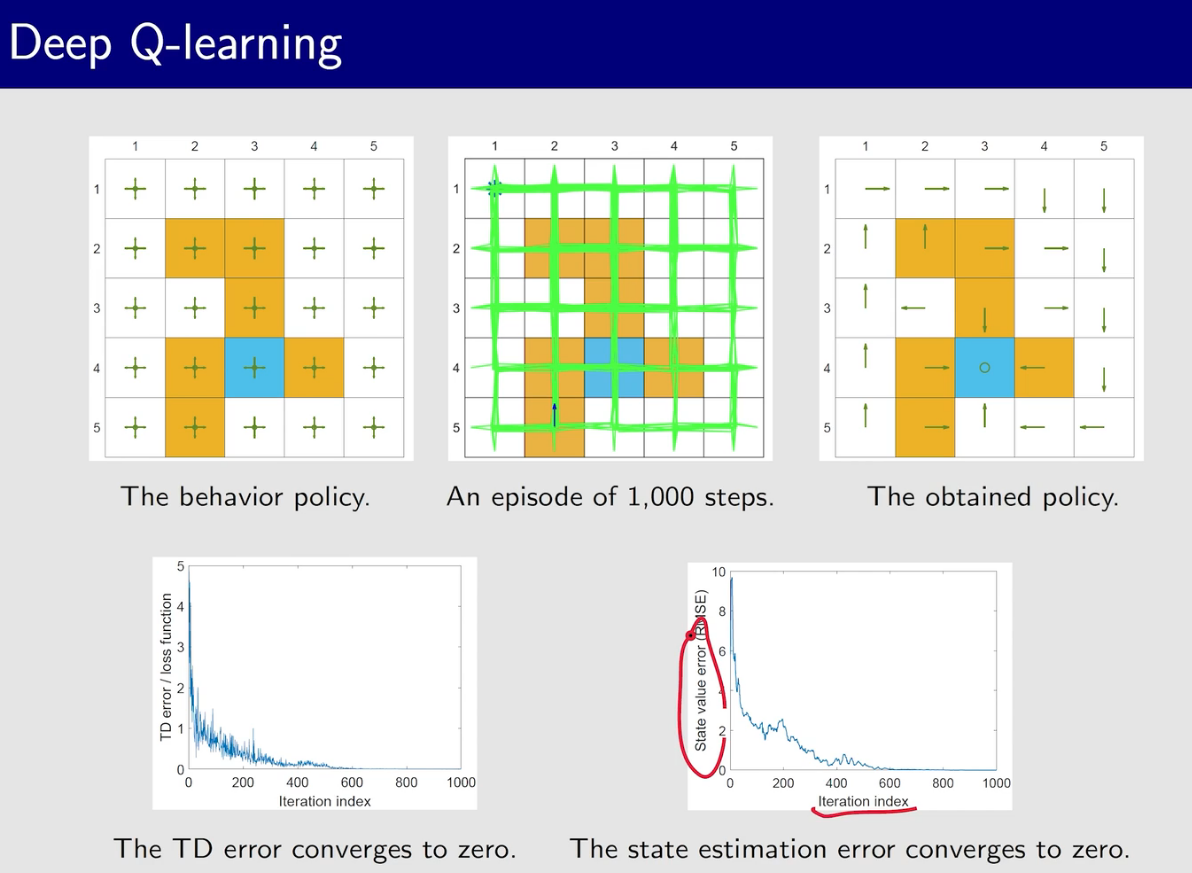
与原论文中的有些出入，原论文中用了更多的技巧，效果也更好些

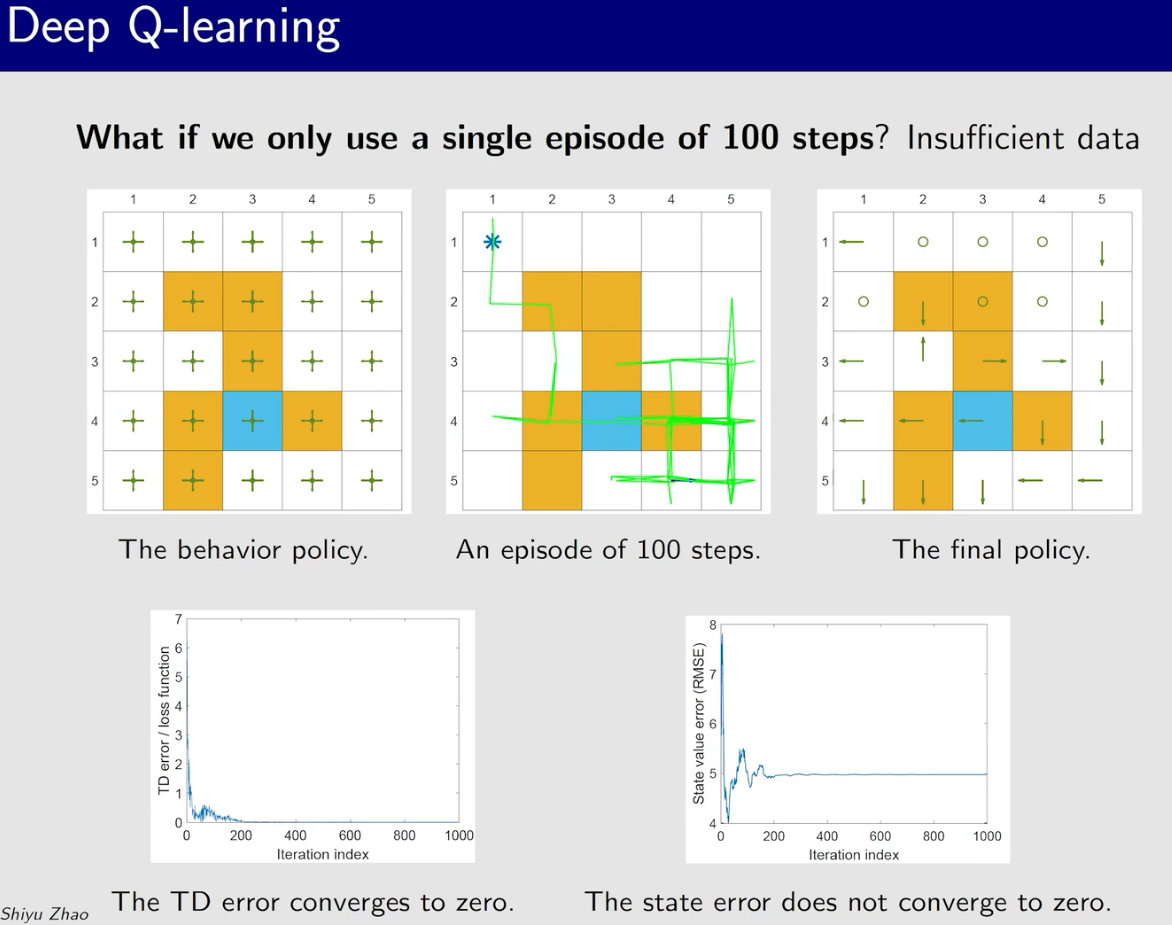
策略梯度方法

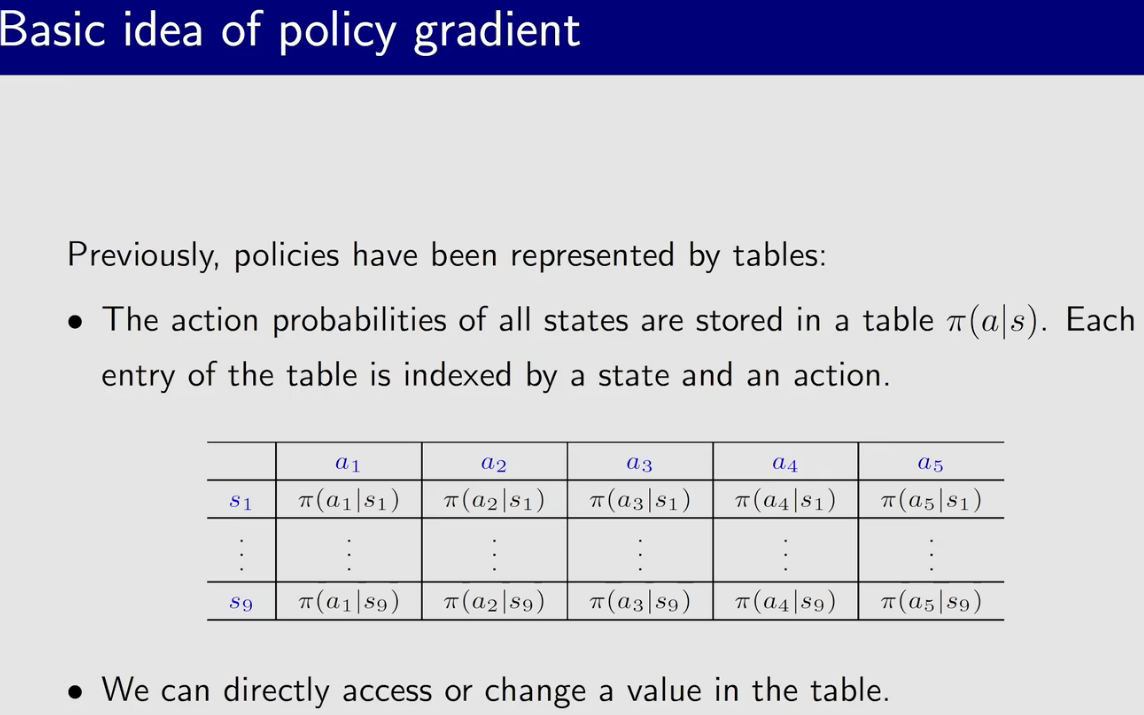
Actor-Critic方法