【王树森】深度强化学习(DRL)
注:以下内容中,大写的为随机变量,小写的为观测值
强化学习基础
Terminologies
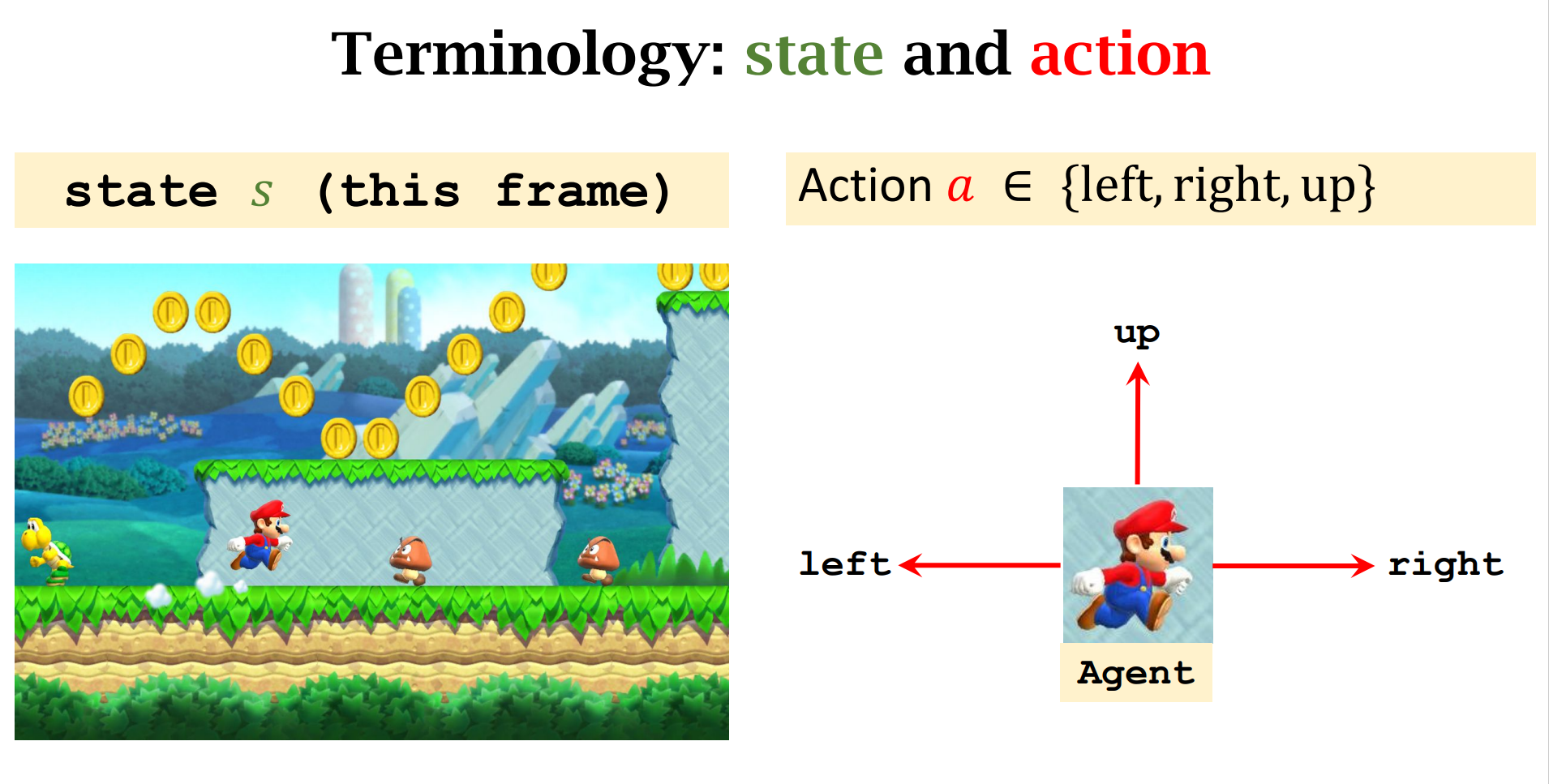
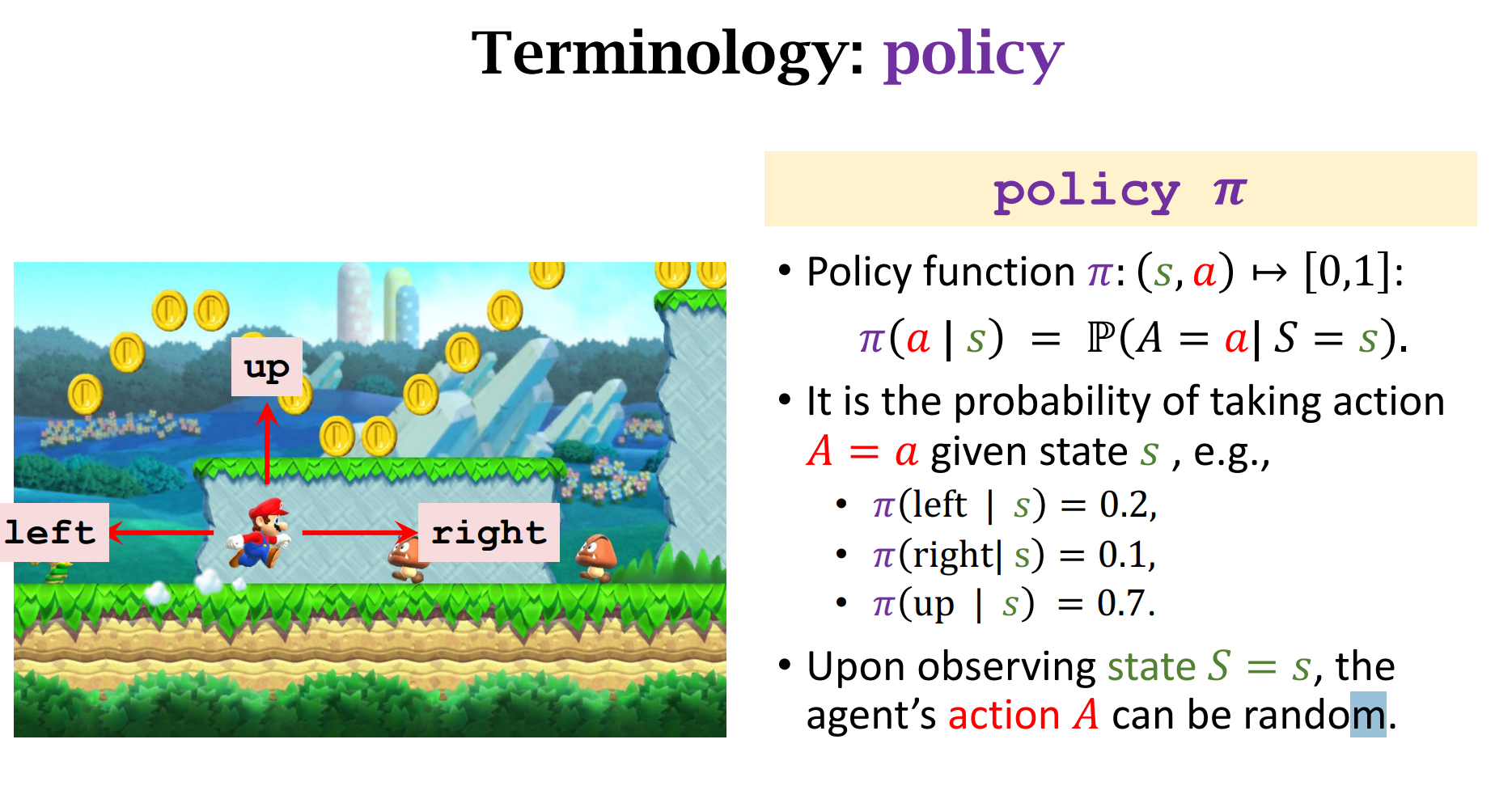
这里$\pi$ 是一个离散的概率密度,在当前状态$s$的情况下,做出$a$动作的概率
强化学习的目标就是获得的奖励尽量要高

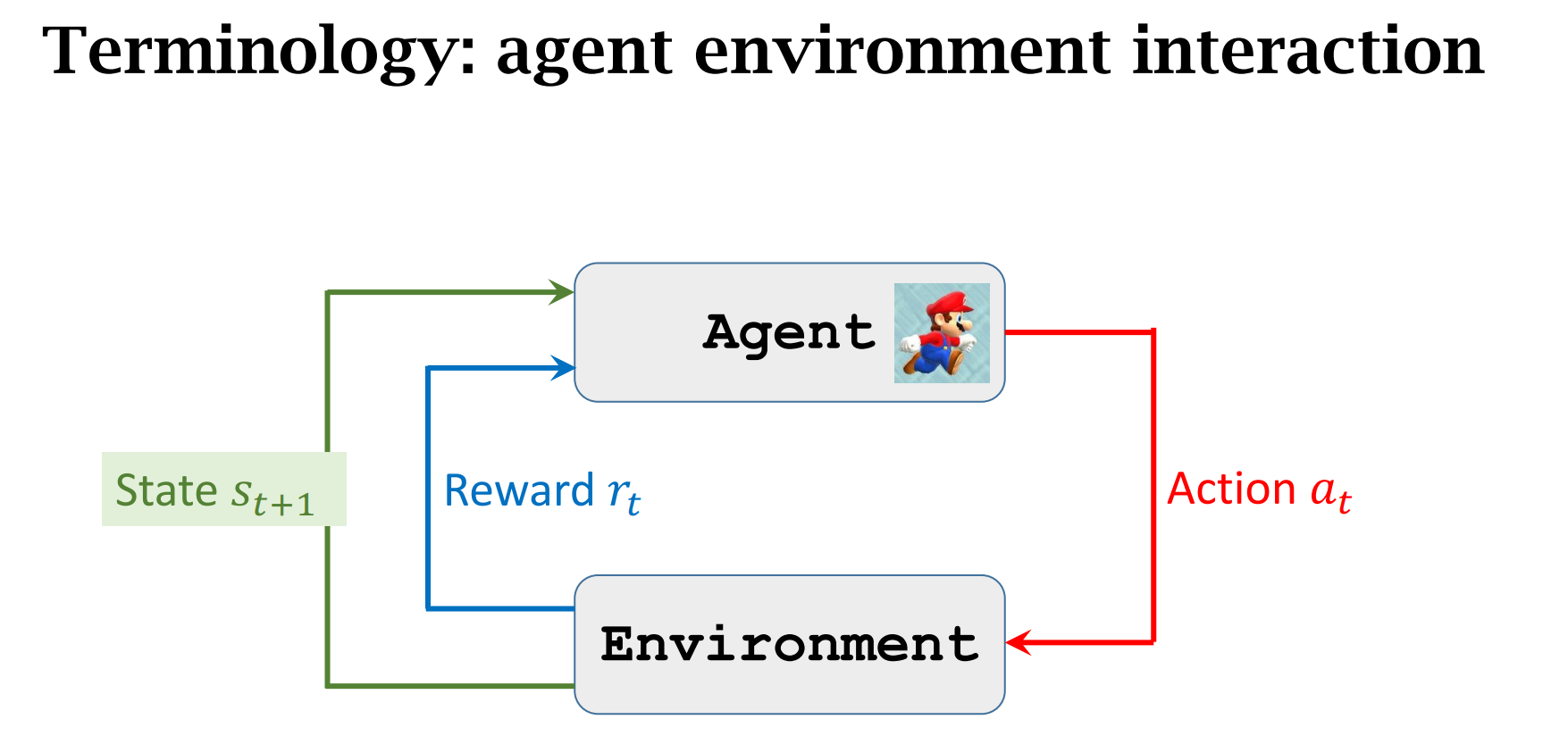
agent与enviroment交互
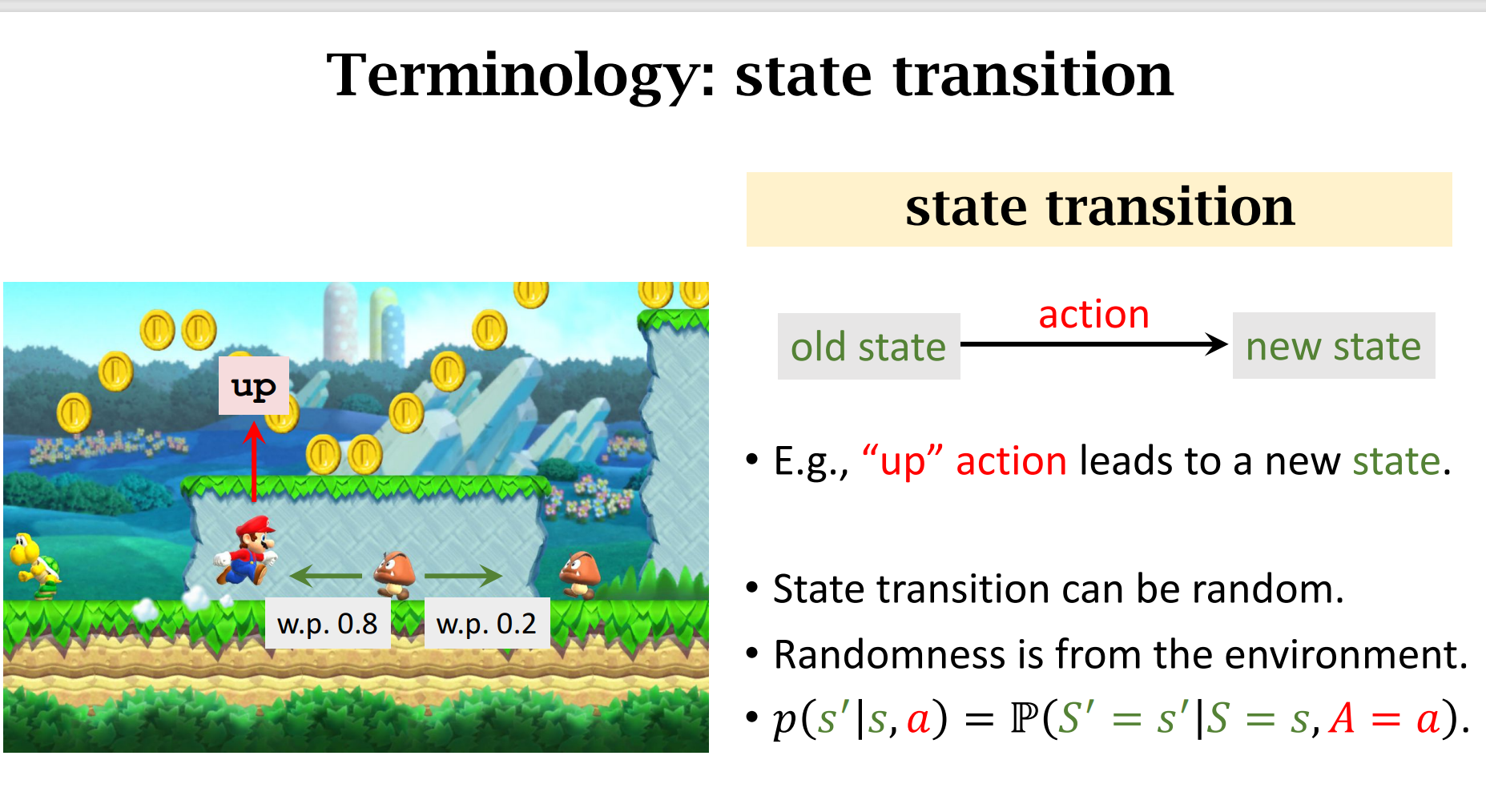
强化学习的随机性
动作的随机性 and 状态转移的随机性


过程
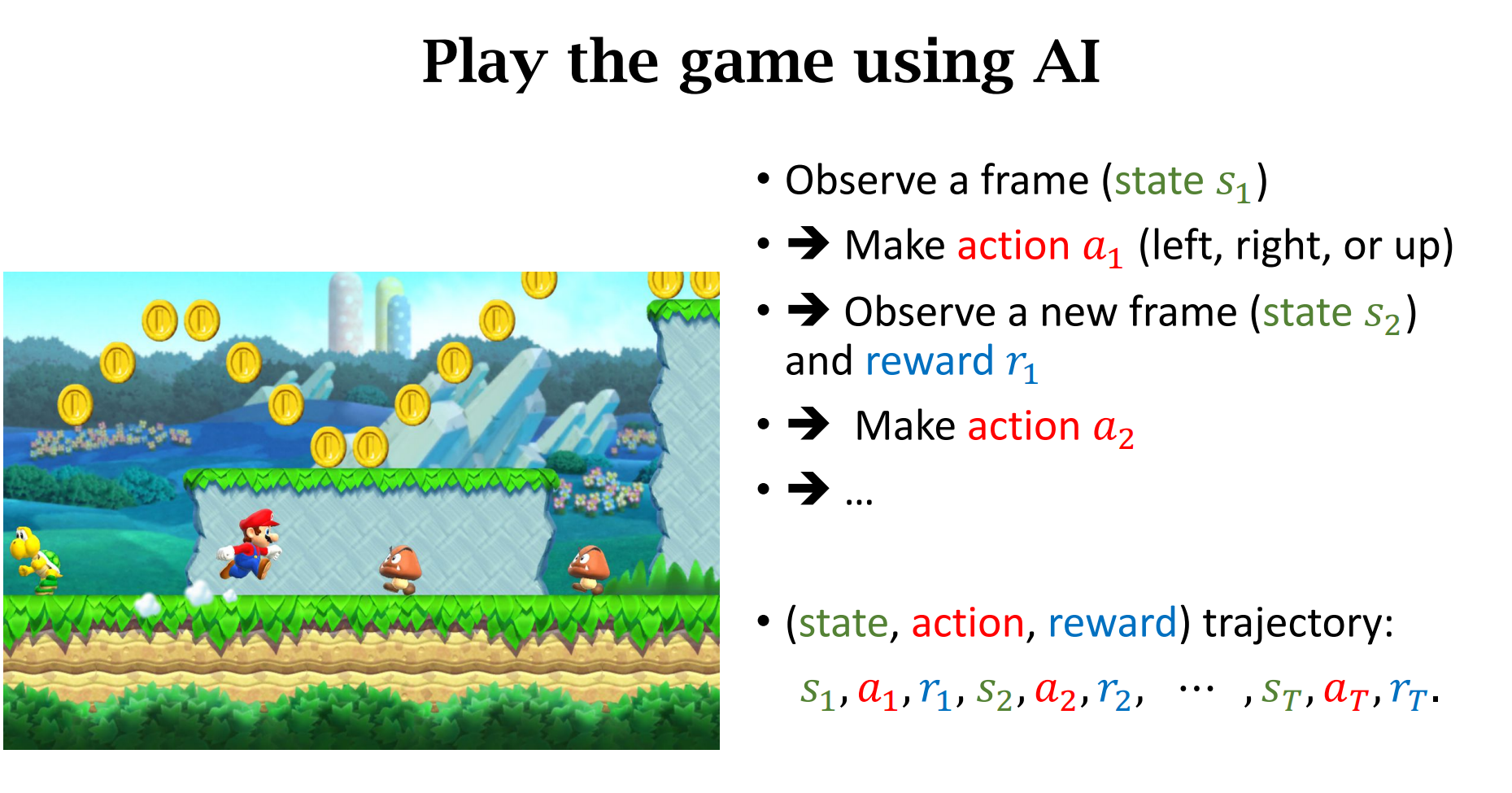
Reward and Return(回报)

引入$\gamma$作为”折扣”


Value Function
- 行动价值函数(Action-Value Function)
- 状态价值函数(State-Value Function)
$U_t$依赖于未来$S_t,S_{t+1},S_{t+2}… and\ A_t,A_{t+1}…$,是一个随机变量

行动价值函数$Q_{\pi}$ 和策略$\pi$有关,它是对随机变量$U_t$求条件期望得到的一个数;最优行动价值函数$Q^*$是所有$\pi$中,让$Q$最大的那个$\pi$

状态价值函数可以对某一局面进行打分

它对$Q_{\pi}$中的A求期望消掉A


Summarize

基于策略或者基于价值

检验平台-Gym


render()渲染,展示环境

Summary

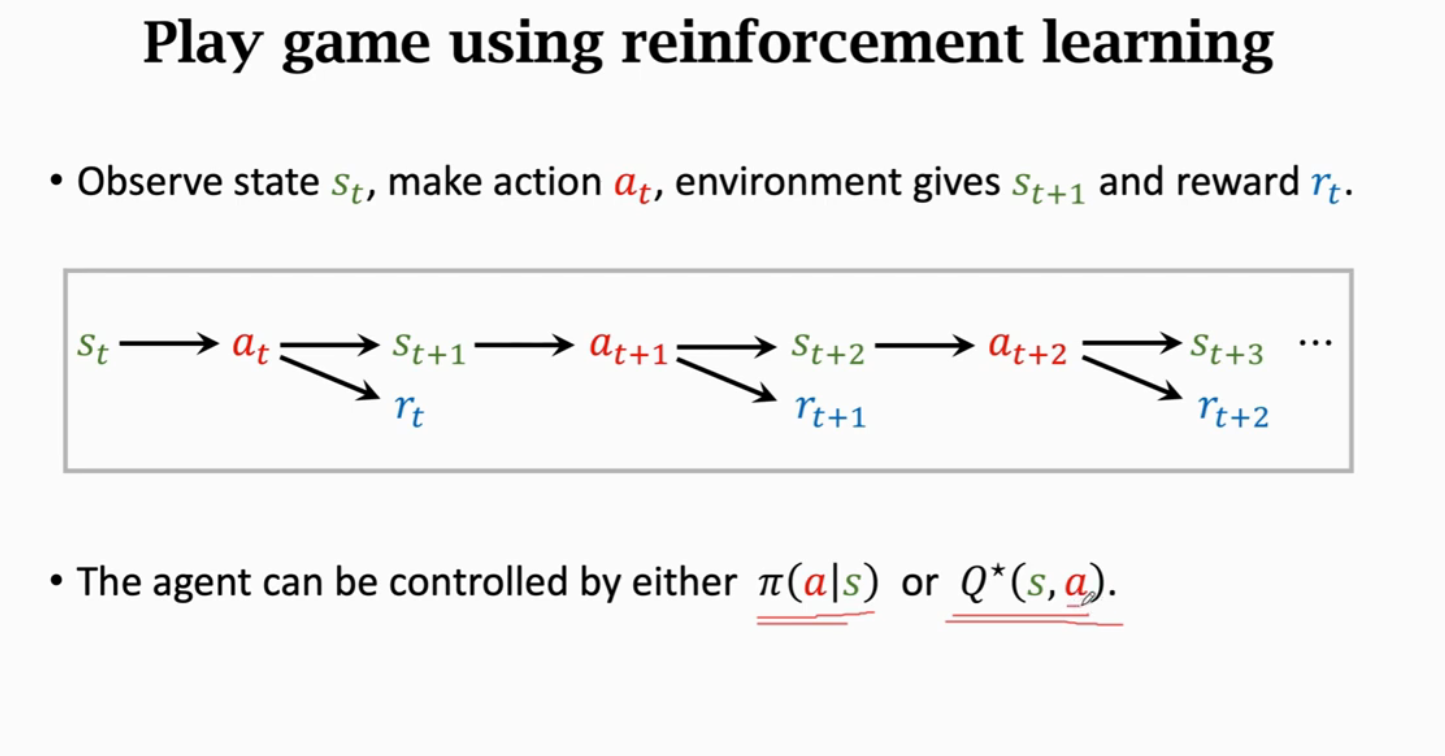

价值学习(Value-Based)
上节课我们学习了行动价值函数(Action-Value)
$U_t$是一个随机变量,依赖于将来的行动Action和状态S,我们$U_t$求期望,消除未来的影响,使得$Q_{\pi}(s_t,a_t)$依赖于$s_t,a_t,\pi$。

进一步,我们可以求$\pi$最大化,求最优状态价值函数$Q^*$ ,$Q^*(s_t,a_t)$意味着在$s_t$状态加,做出行动$a_t$所得到的价值分数

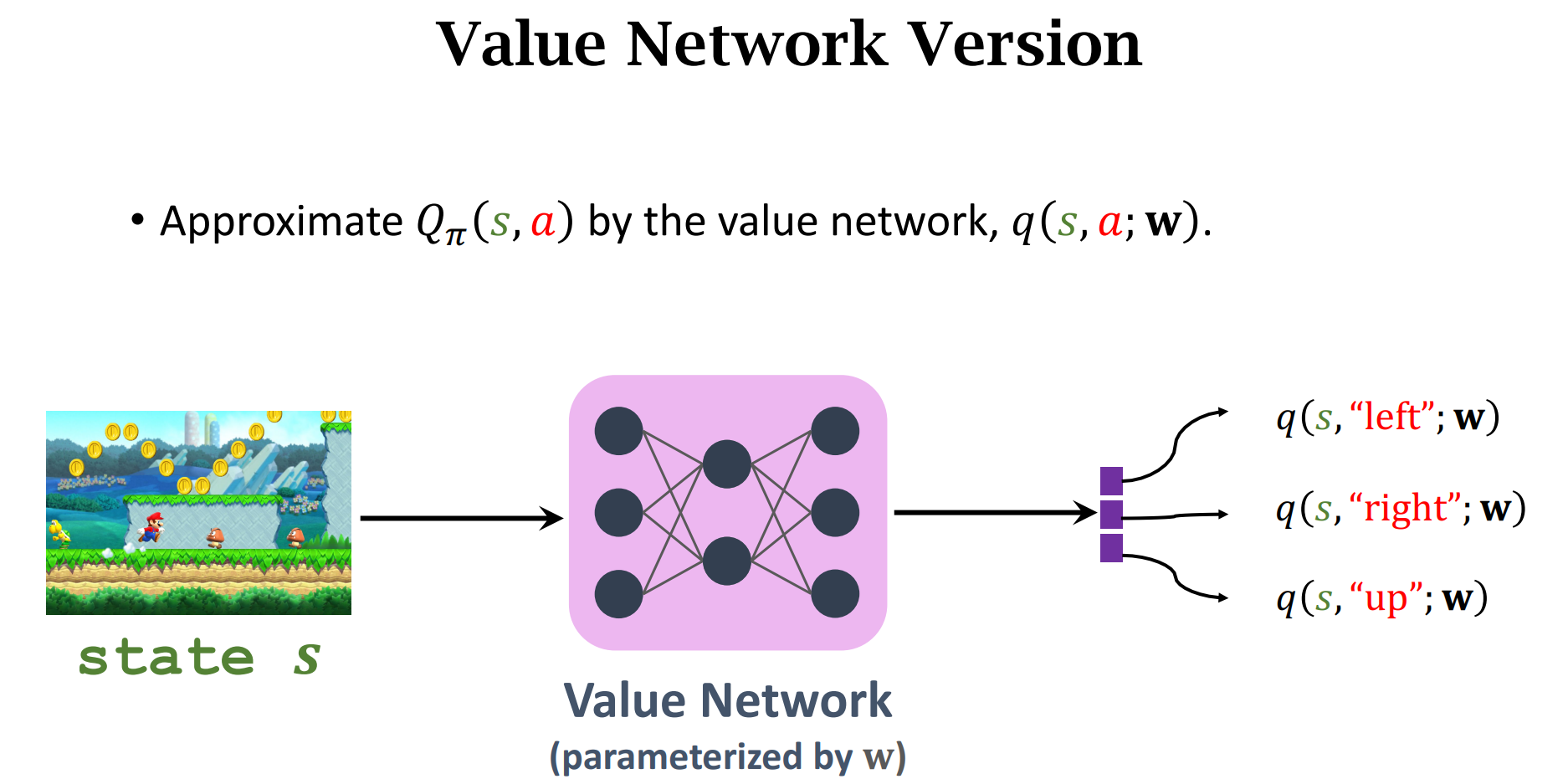
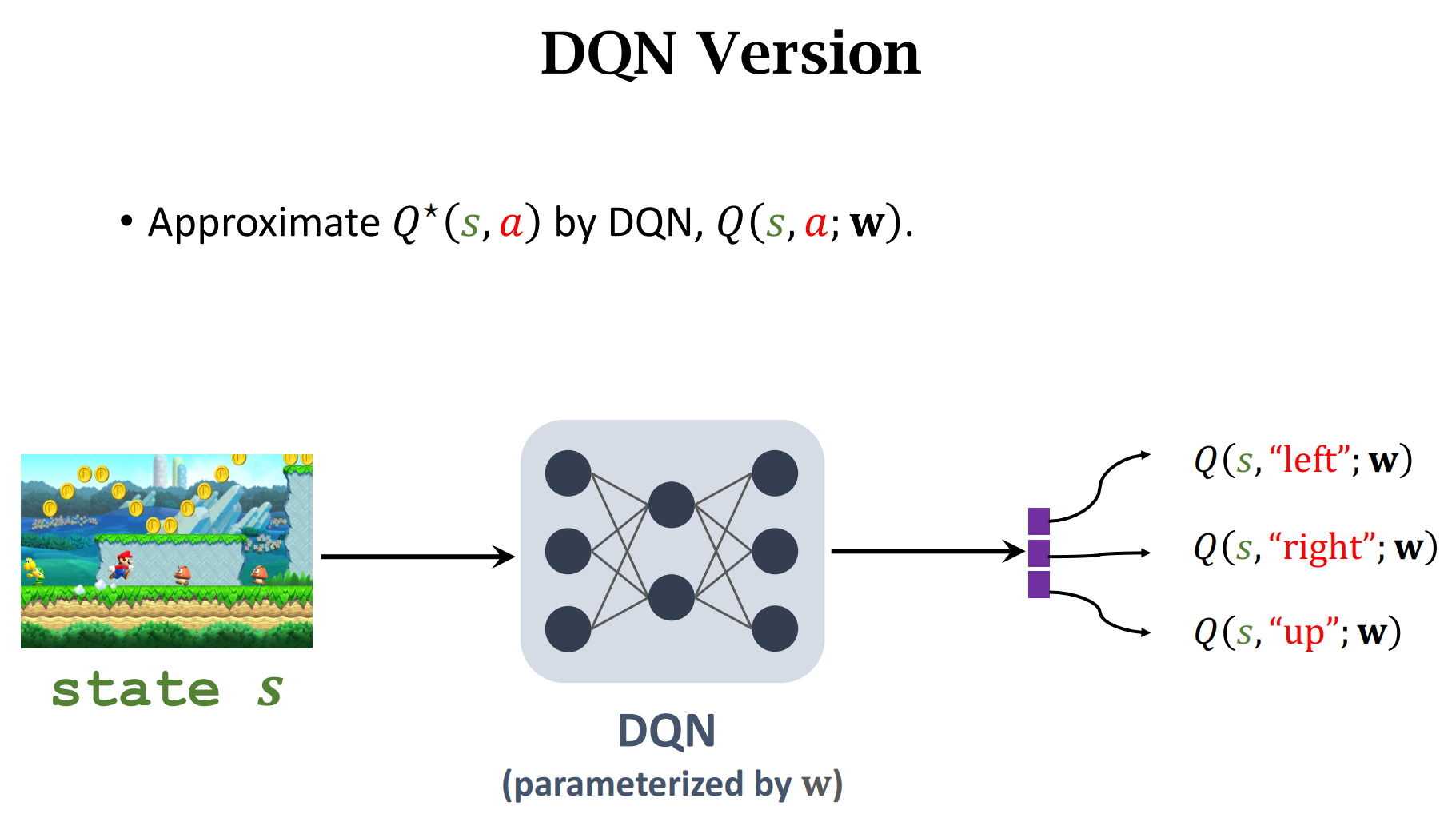
DQN(Deep Q-Network (DQN))

$Q(s,a;w)$ :神经网络的参数是$w$,输入是$s$,输出是做出动作$a$的价值分数

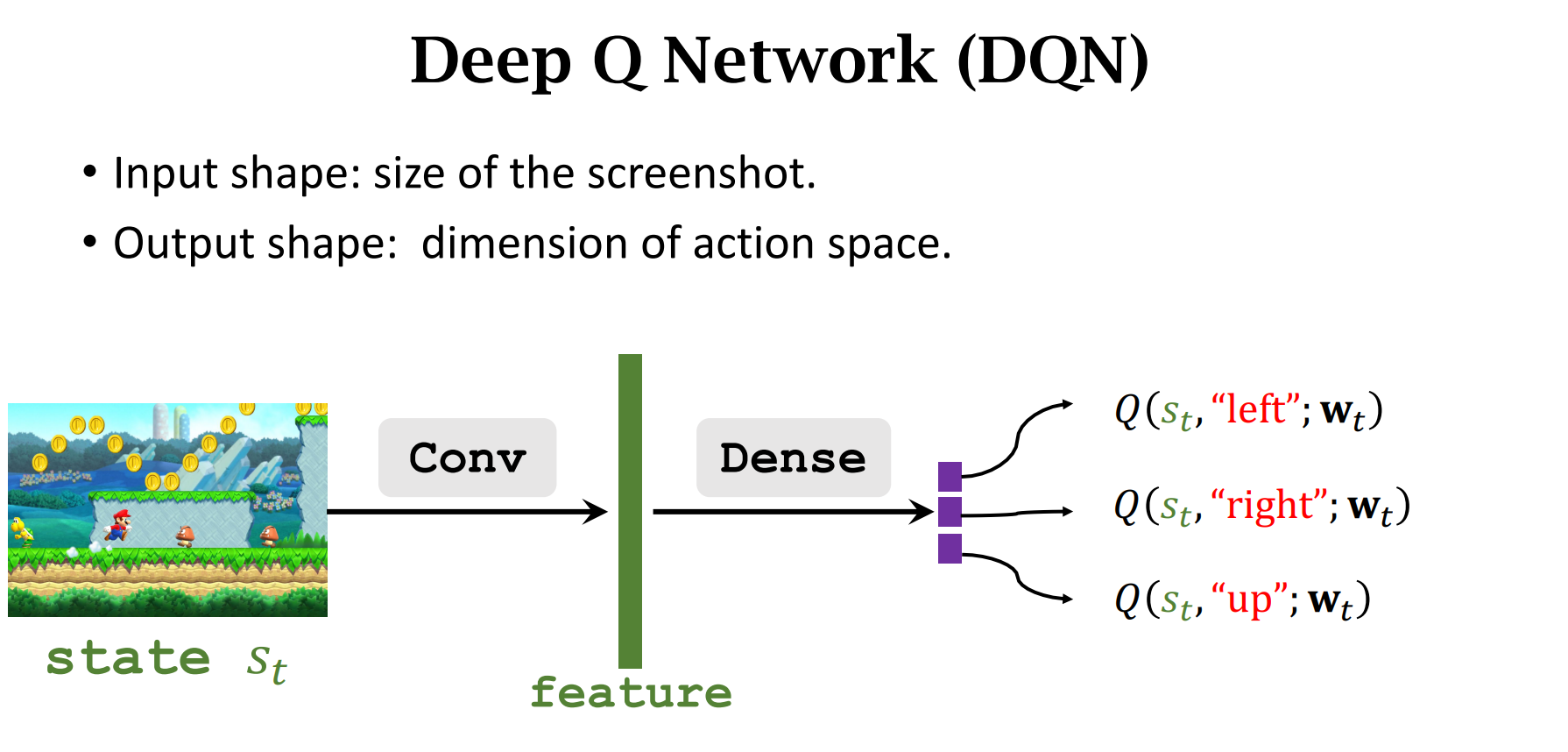
做出动作$up$的价值分数最高,所以选择$up$,然后状态转移函数$p(|)$会人random一个新的状态
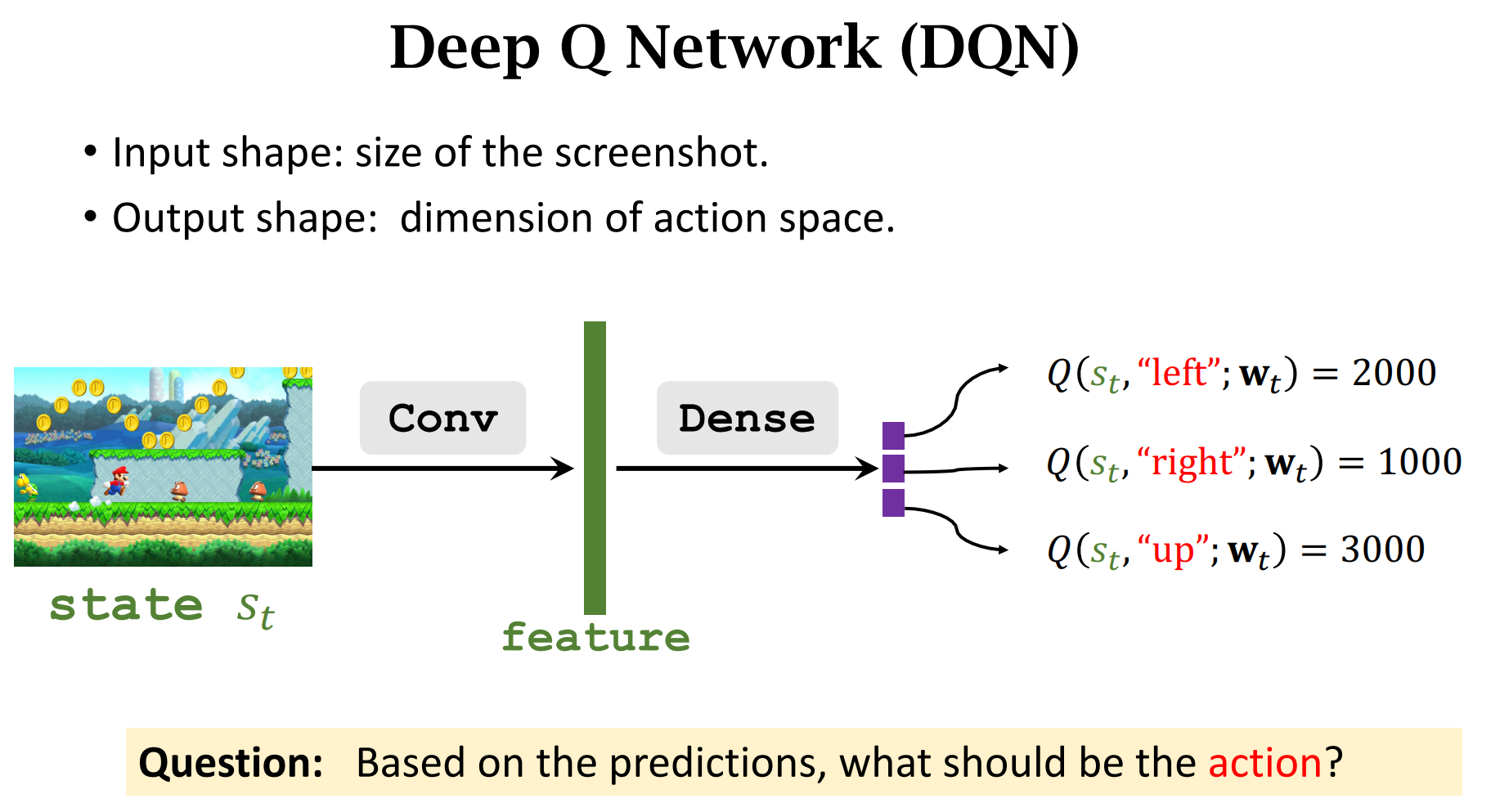
根据输入$s_t$,选择价值分数最大的动作$a_t$
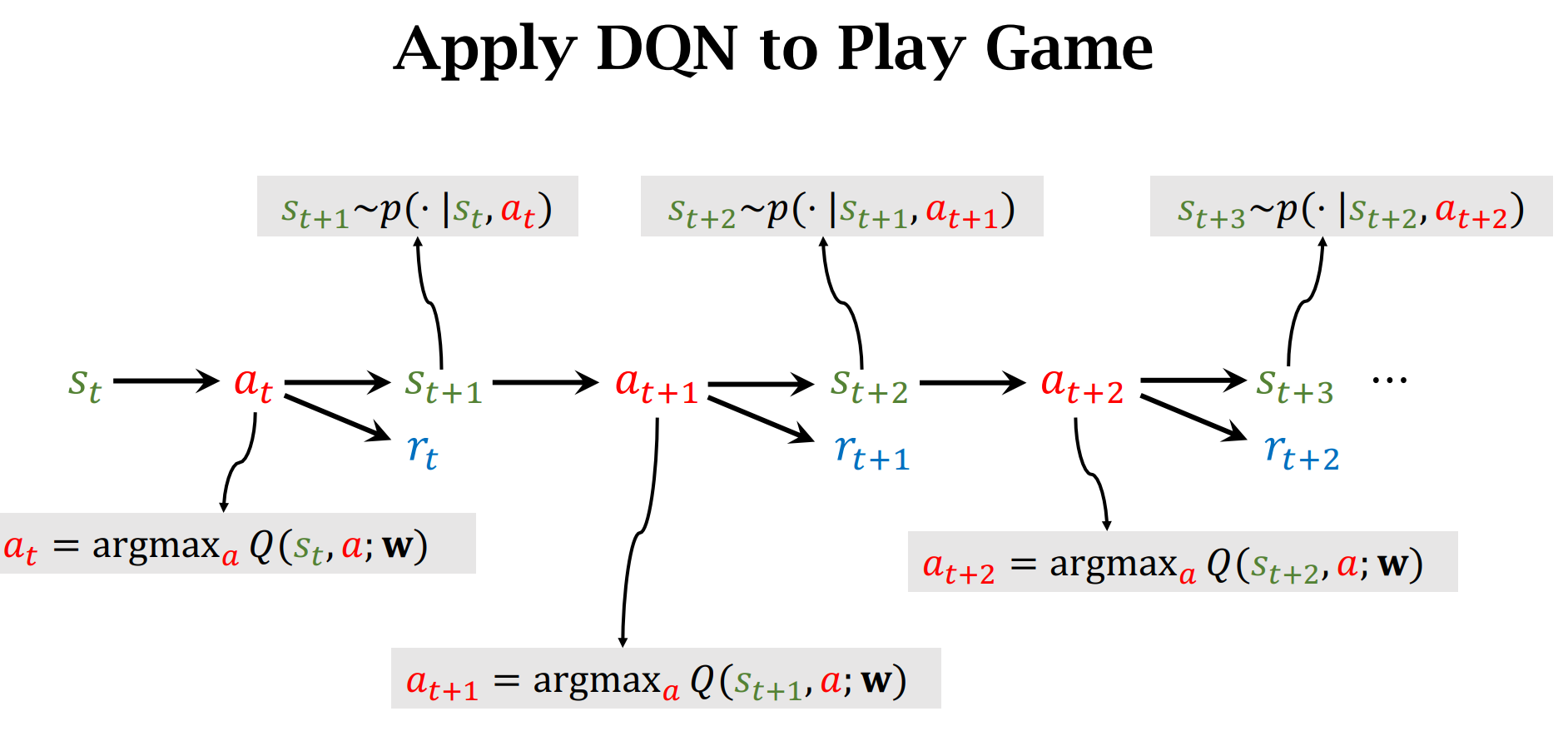
怎么训练DQN?
- TD Learning(不完成旅程也能更新参数)
- Sarsa
- Q-learning
- Multi-Step TD Target
Temporal Difference (TD) Learning



时序差分算法的目标就是让$TD\ Error$尽可能的小,趋近于0

$\gamma$ 是介于0 和 1之间的折扣率





Summary


策略学习(Policy-Based)
策略函数Policy Function

由于输入的状态$s$是多种多样的,所以我们可以用一个函数来近似
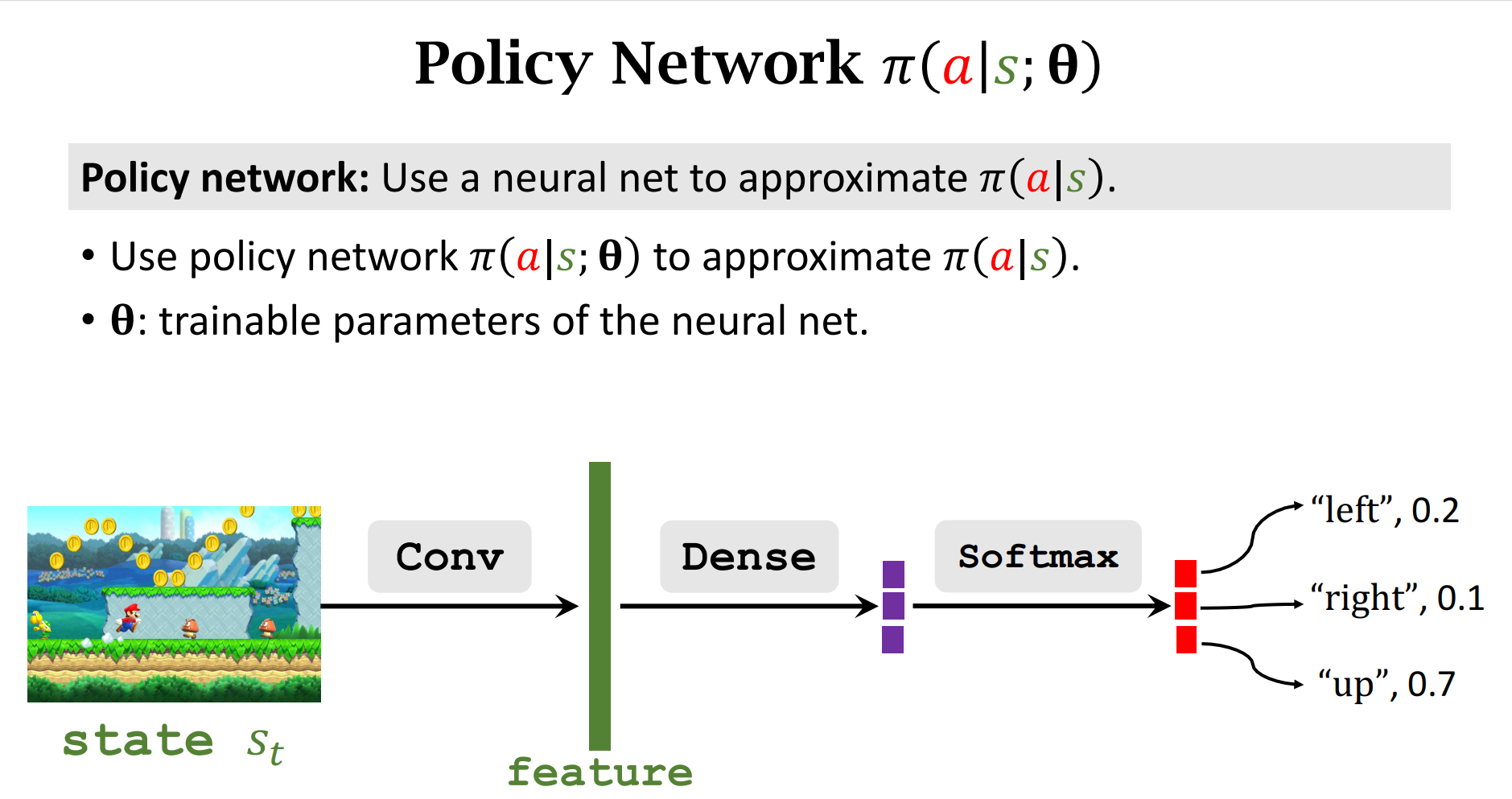
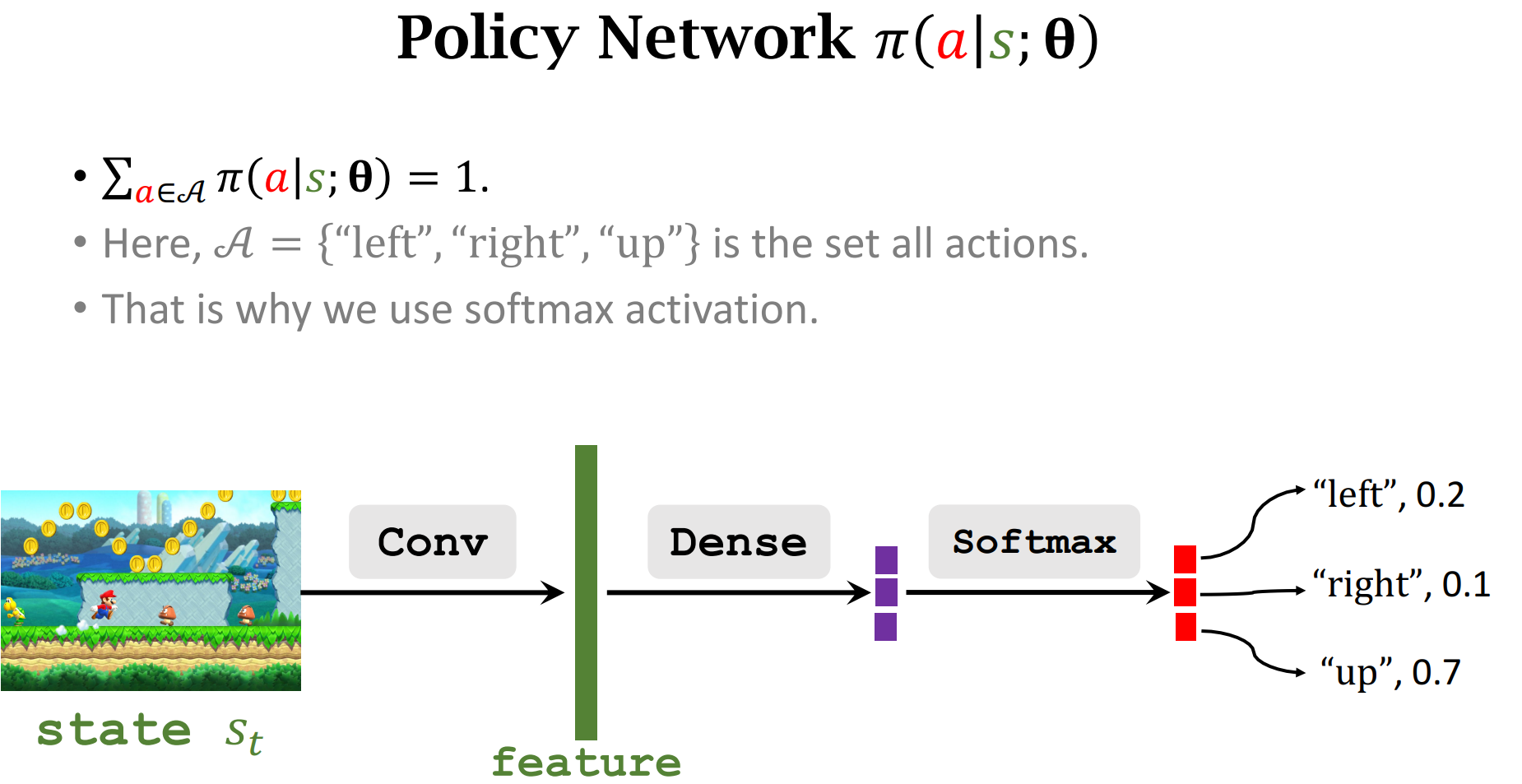
策略梯度


这里我的理解是:选择最优的策略动作,才能最大化状态价值函数$V(s;\theta)$,所以现在我们的目的变为了最大化$V(s;\theta)$,我们用梯度上升算法来更新$\theta$

Policy Gradient 的推导


这里我们加设$Q_{\pi}$函数与$\theta$无关,但实际上是有关的,所以这里推导是不严谨了,但是方便理解






因为神经网络是一个很复杂的函数,我们无法对此进行积分,所以我们用蒙特卡洛方法进行近似

因为$g(\widehat{a},\theta)$是策略梯度的无偏估计,所以我们用它来近似策略梯度


Summary For 策略梯度算法(梯度上升更新$\theta$)




Summary

Actor-Critic Methods
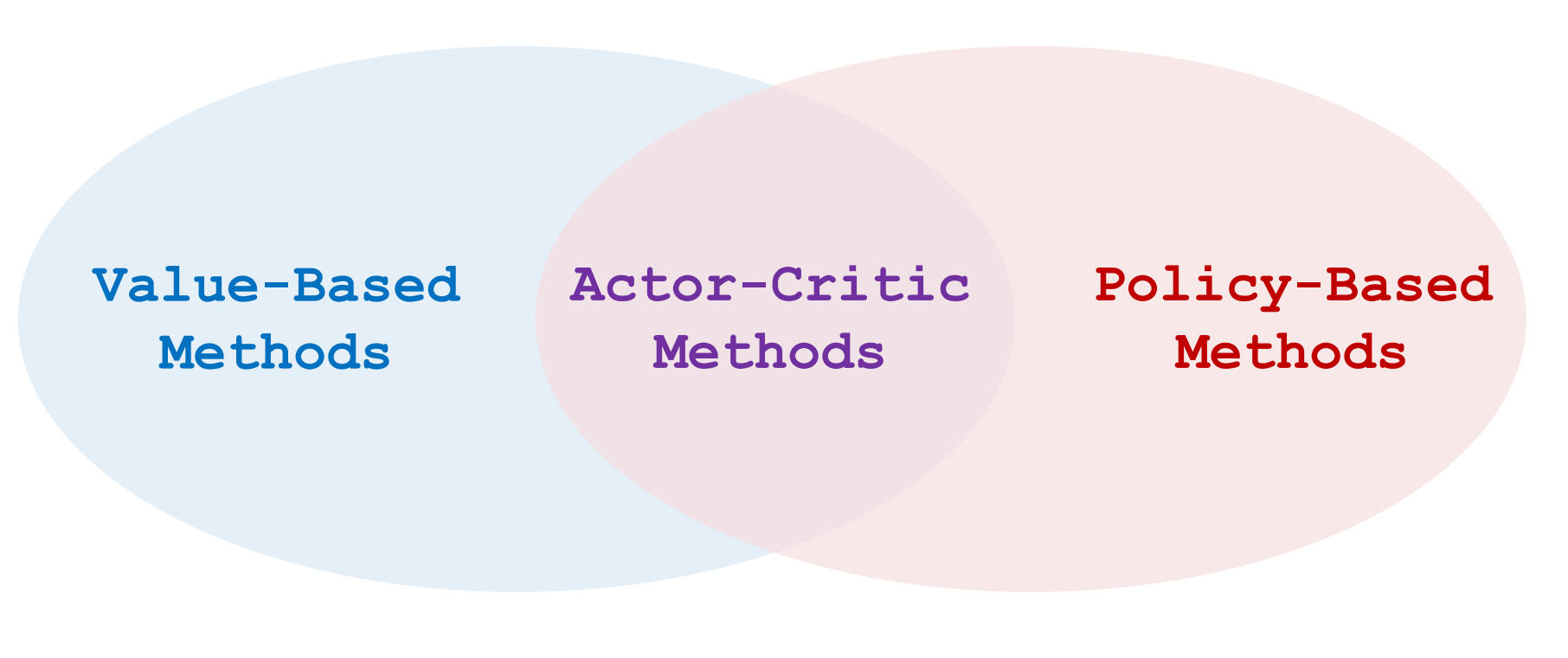
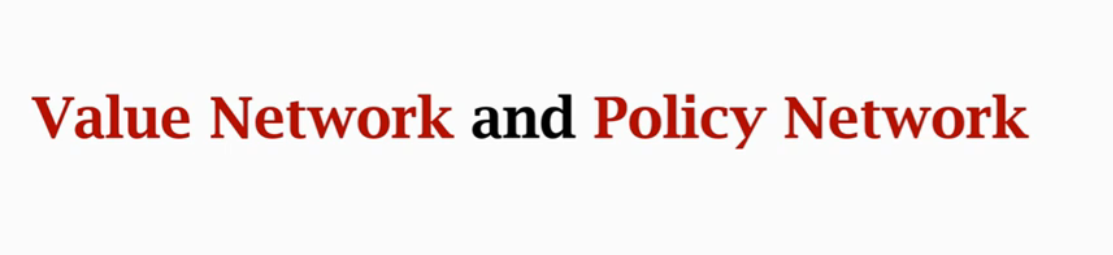

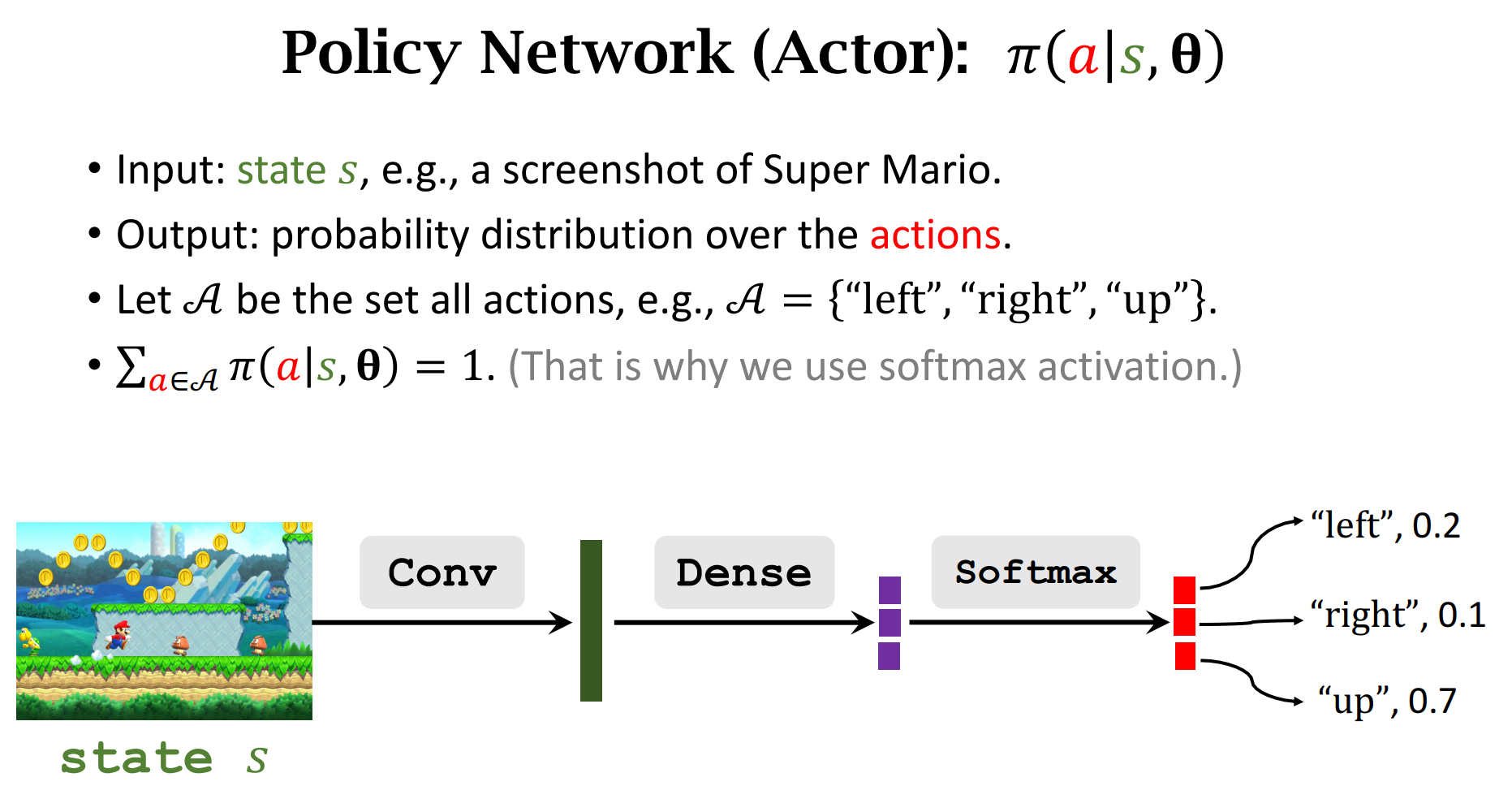
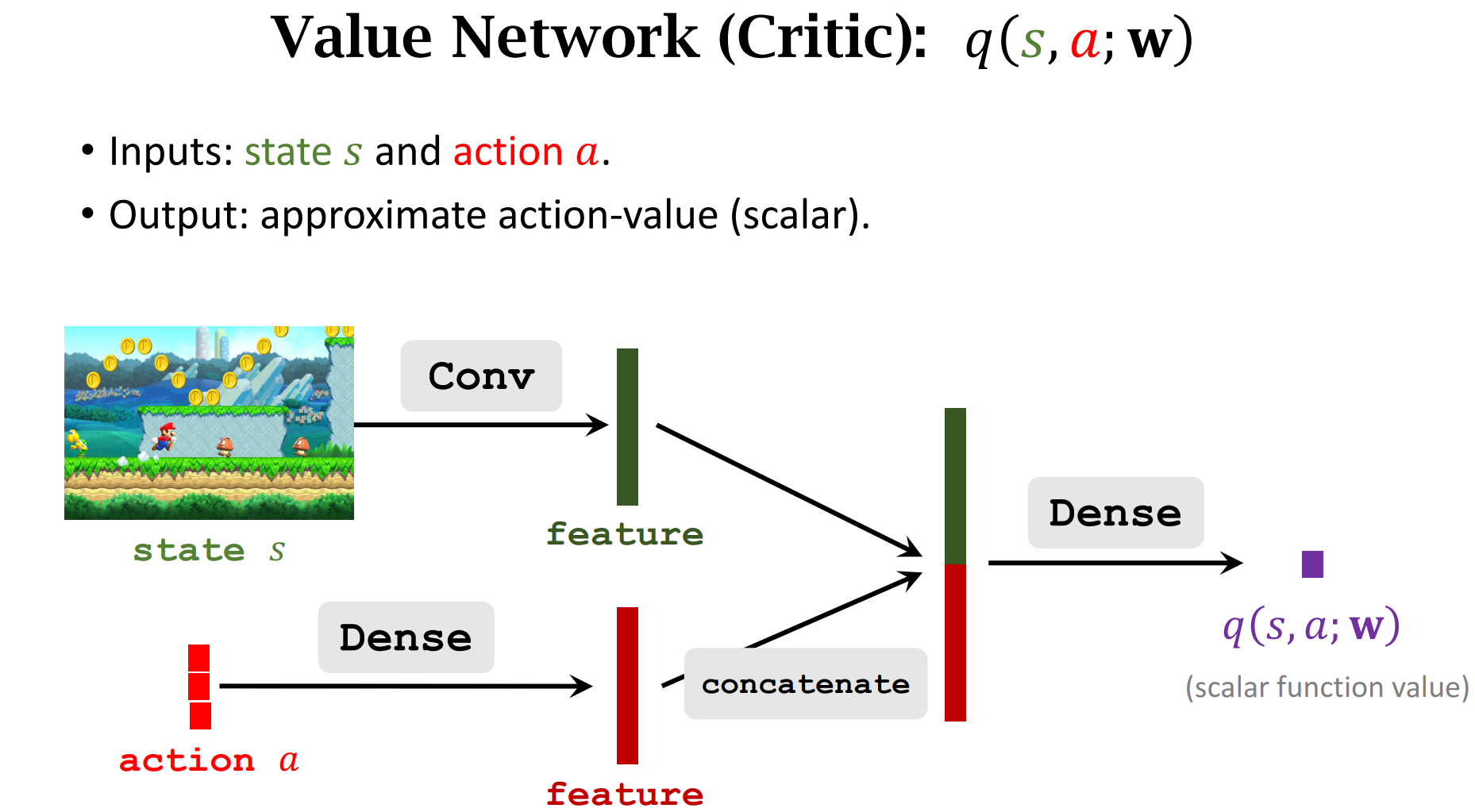
让运动员的平均分越来越高,并且让裁判的打分越来越精准





图解
运动员根据$state$做出$Action$
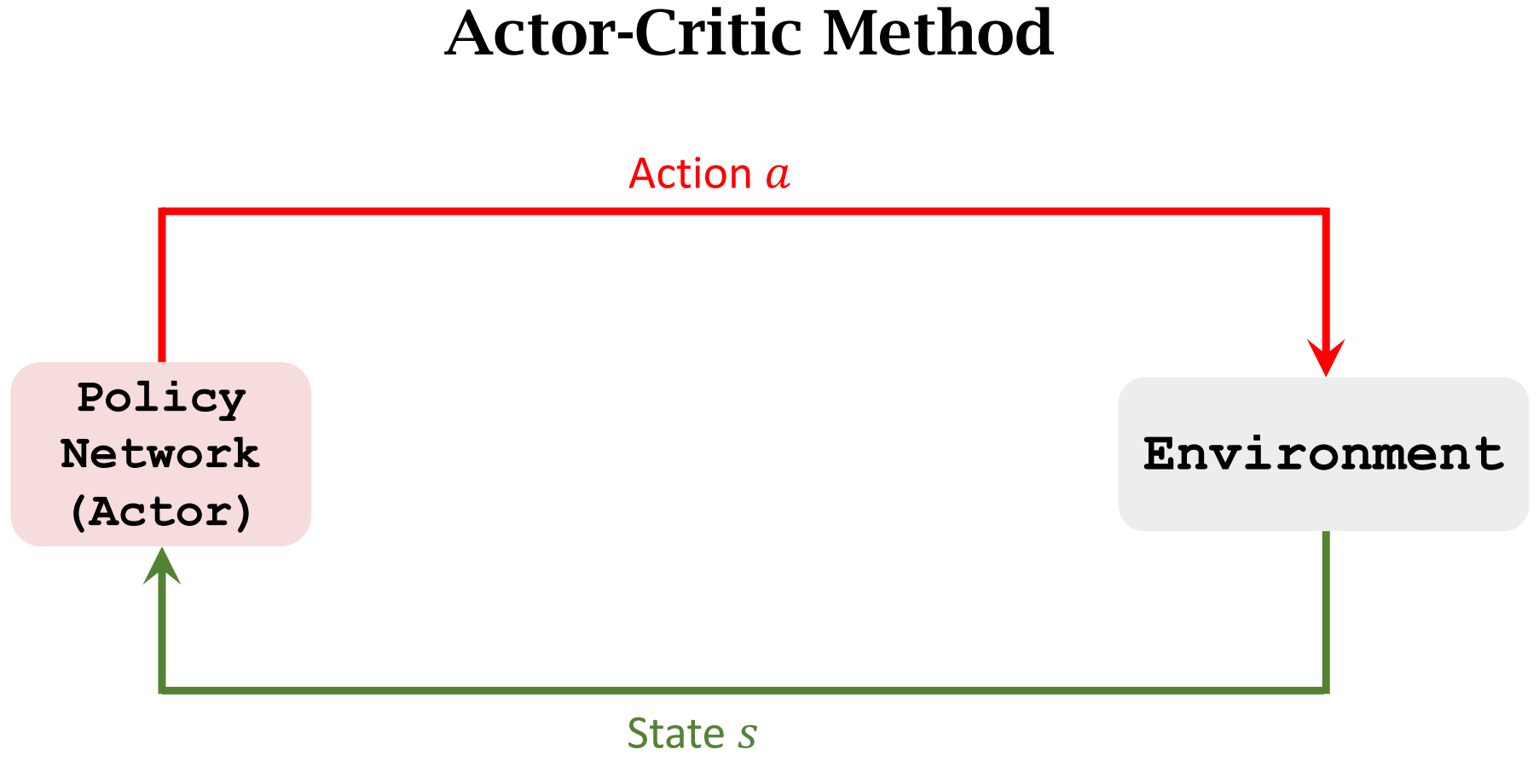
裁判会根据做出的动作$a$和$state$进行打分,并将分数反馈给运动员
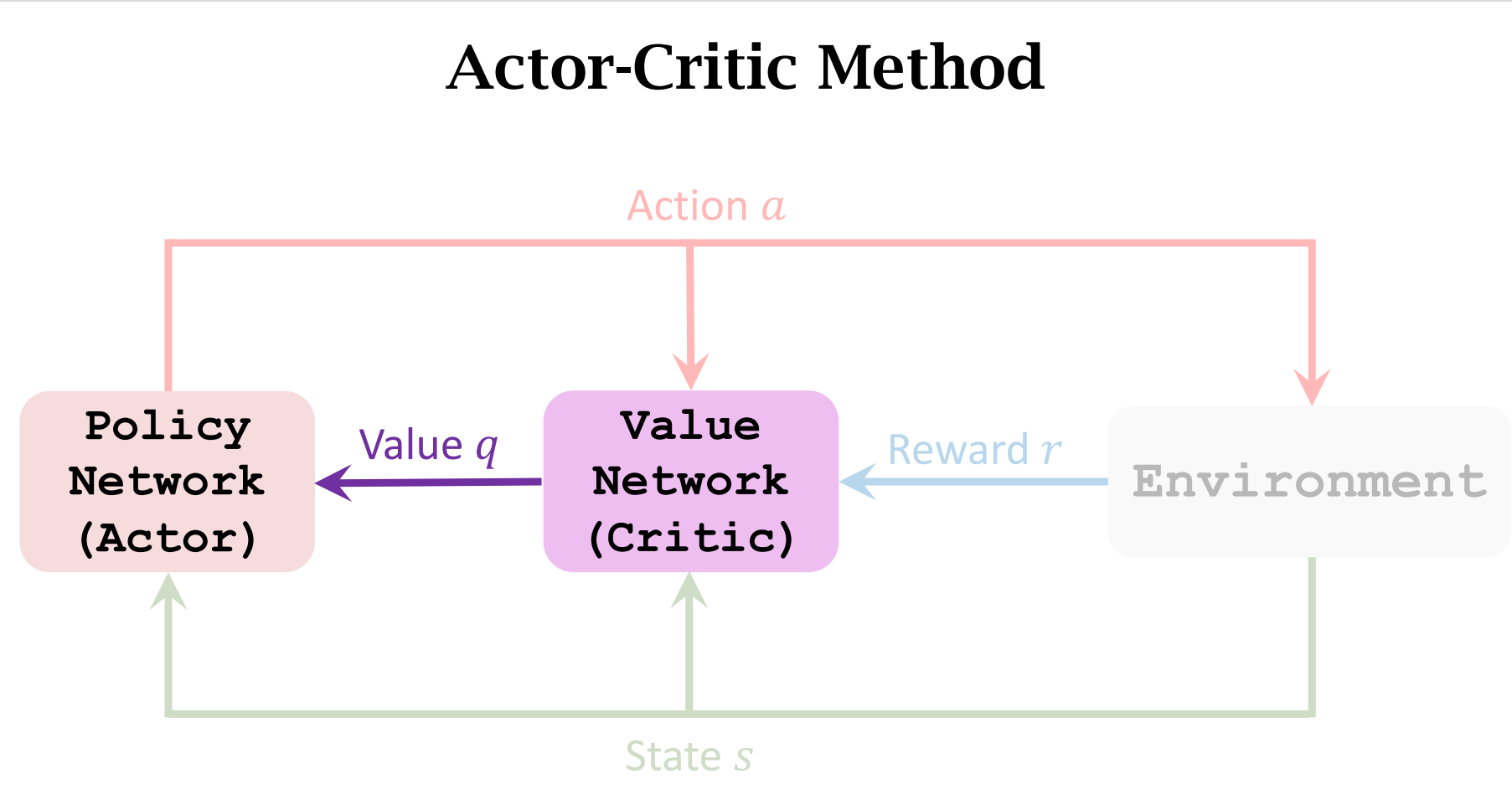
运动员会根据分数来调整自己的动作(迎合裁判)

裁判也会提高自己的水平(根据Reward $r$),以此让运动员做出更好的动作
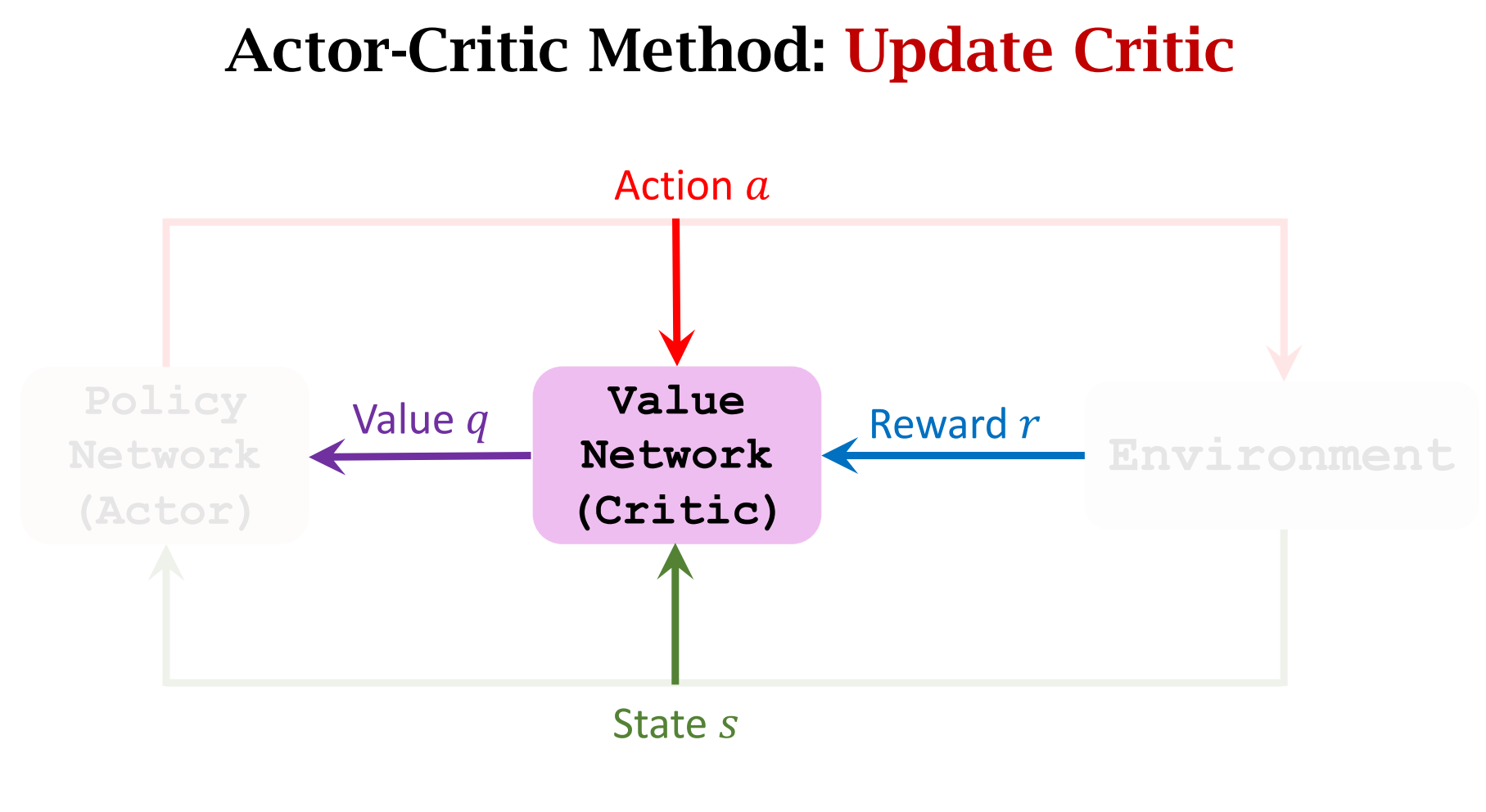
Summary of AC算法

第九步,$q_t$和$\delta_t$ 都对,不过$\delta_t$ 是叫做带baseline的策略梯度算法


Summary



实例分析:AlphaGo的基本原理

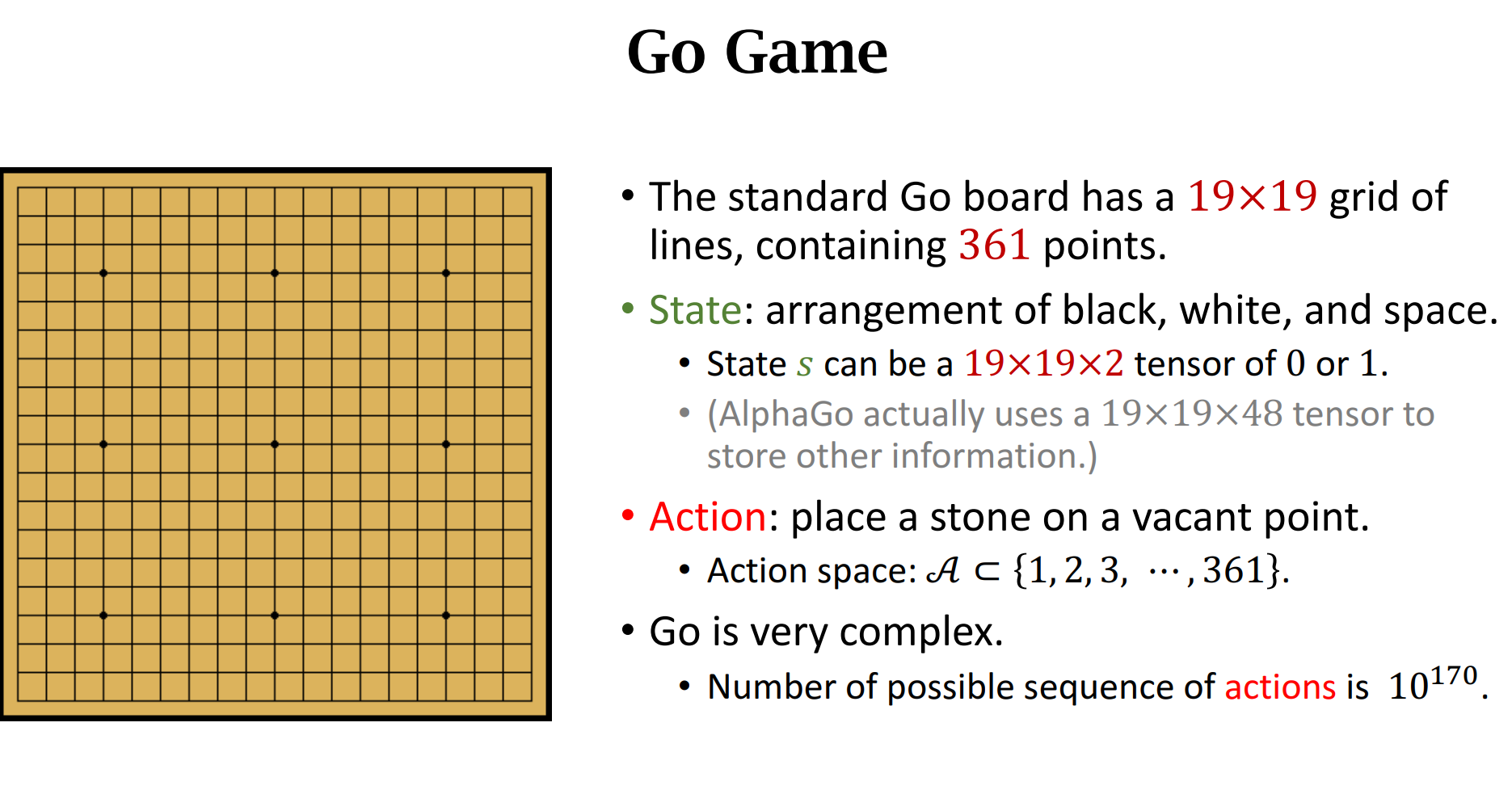



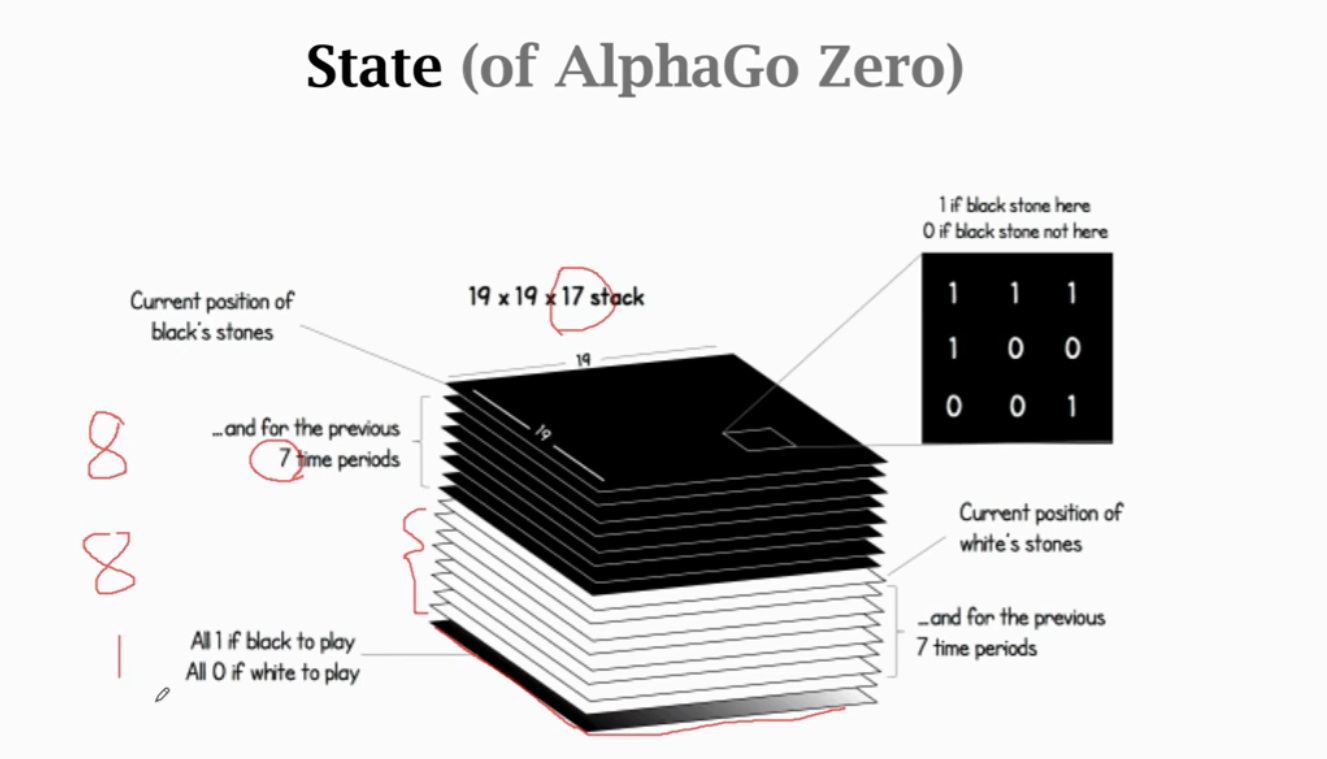
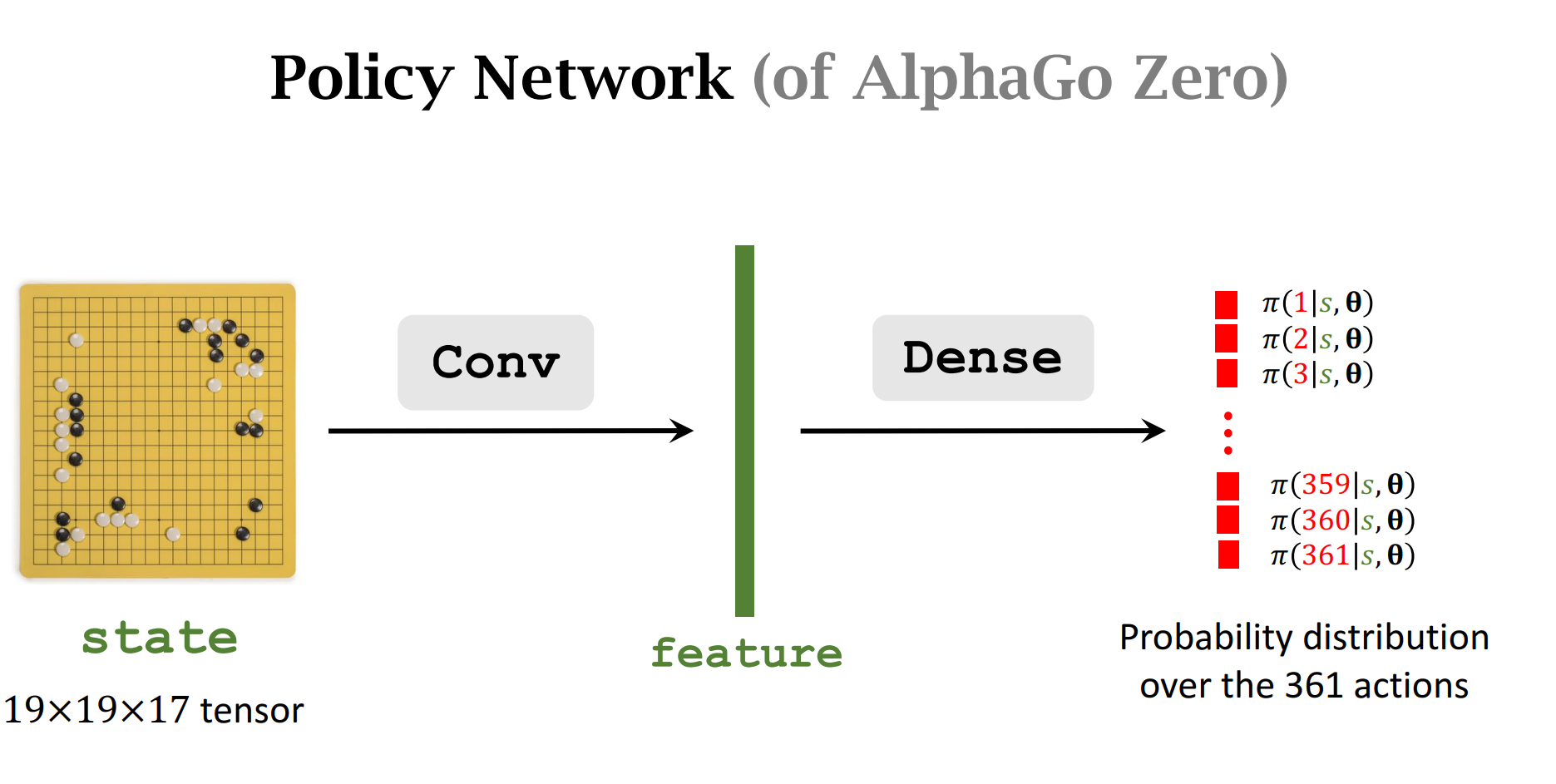
1. Behavior Cloning

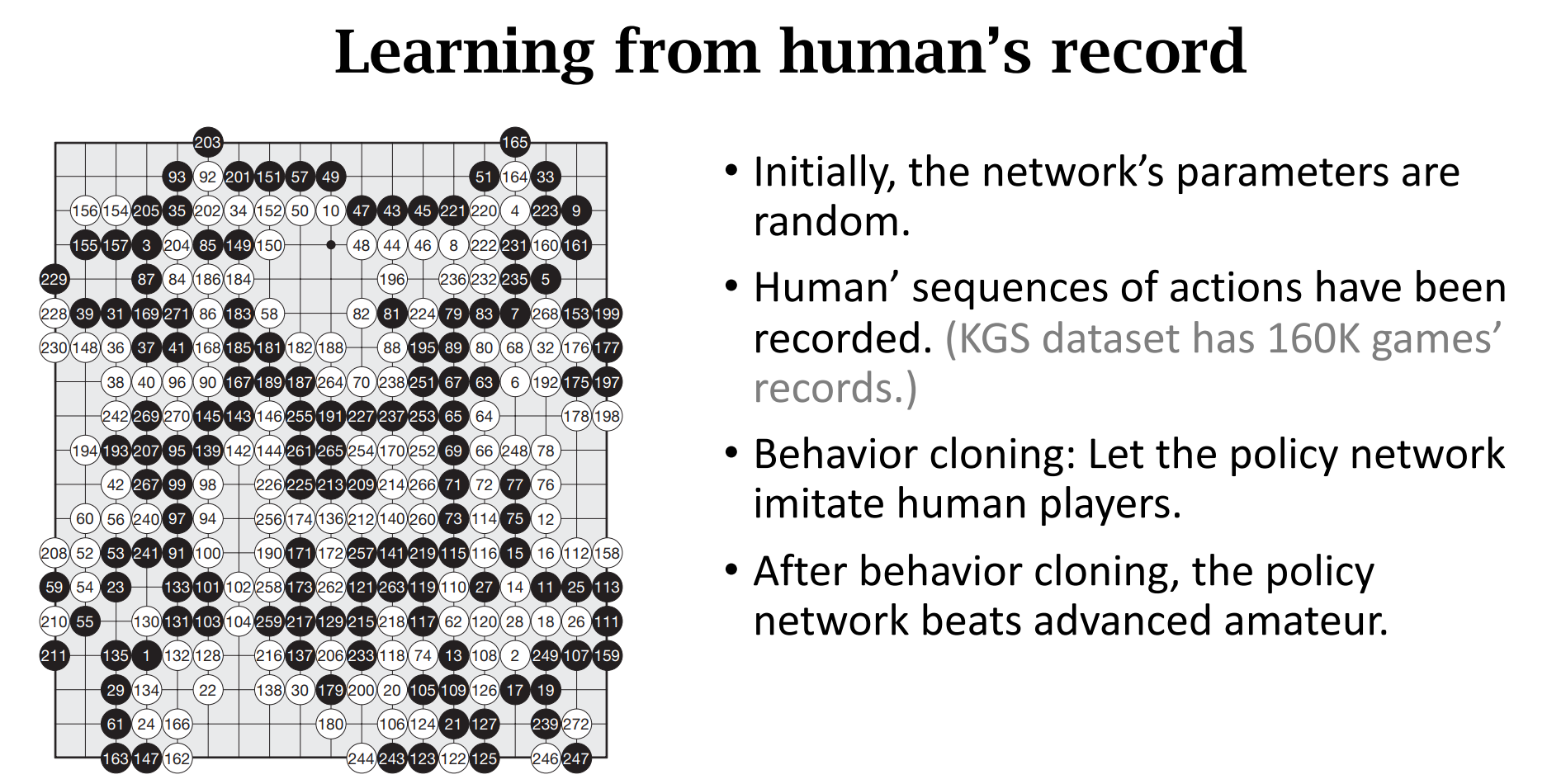


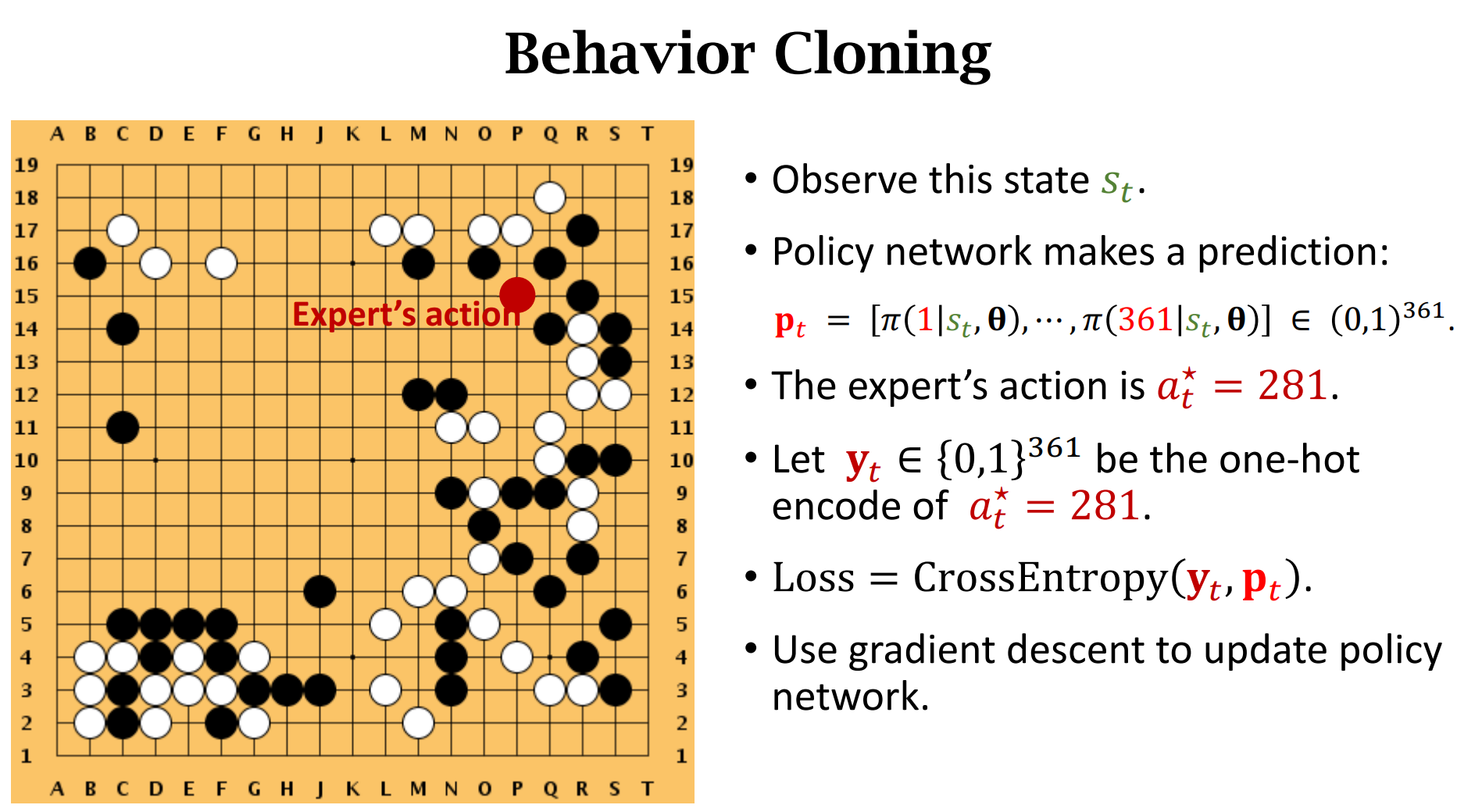

2. 训练策略网络


这里没有折扣,如果赢了,我们认为之前下的每一步棋都是好棋,如果输了,认为每一步棋都是臭棋(没有办法区分一步棋是好是坏)



直接用策略网络还是不够好,所以采用蒙特卡洛树搜索+策略网络的方法

用蒙特卡洛树搜索需要训练一个价值网络,这个价值网络是对$状态价值函数v$的近似,而不是对行动价值Q的近似
3. 训练价值网络


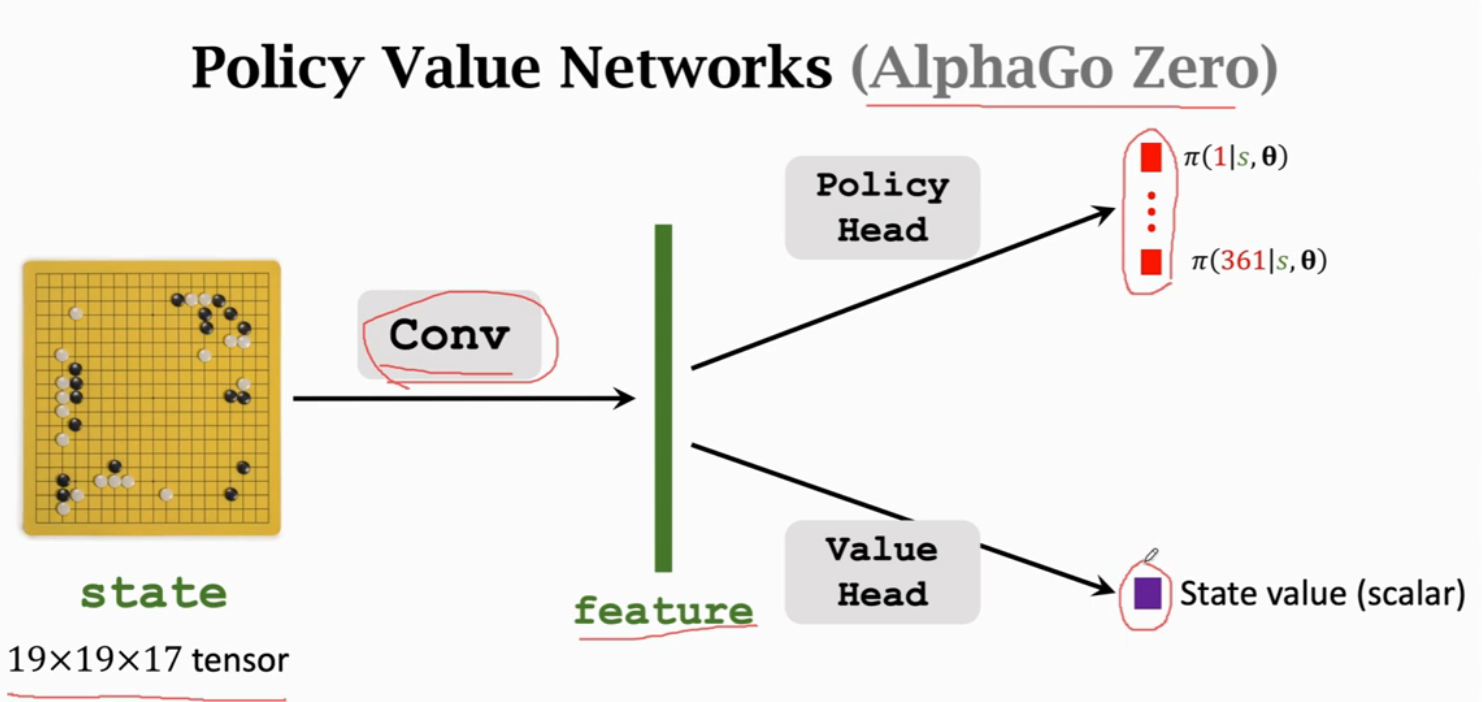
这并不是之前讲的AC算法,这里需要先训练策略网络,然后再根据策略网络训练价值网络。
如下第一步Play a game to the end中用到了策略网络进行博弈

4. 蒙特卡洛树搜索









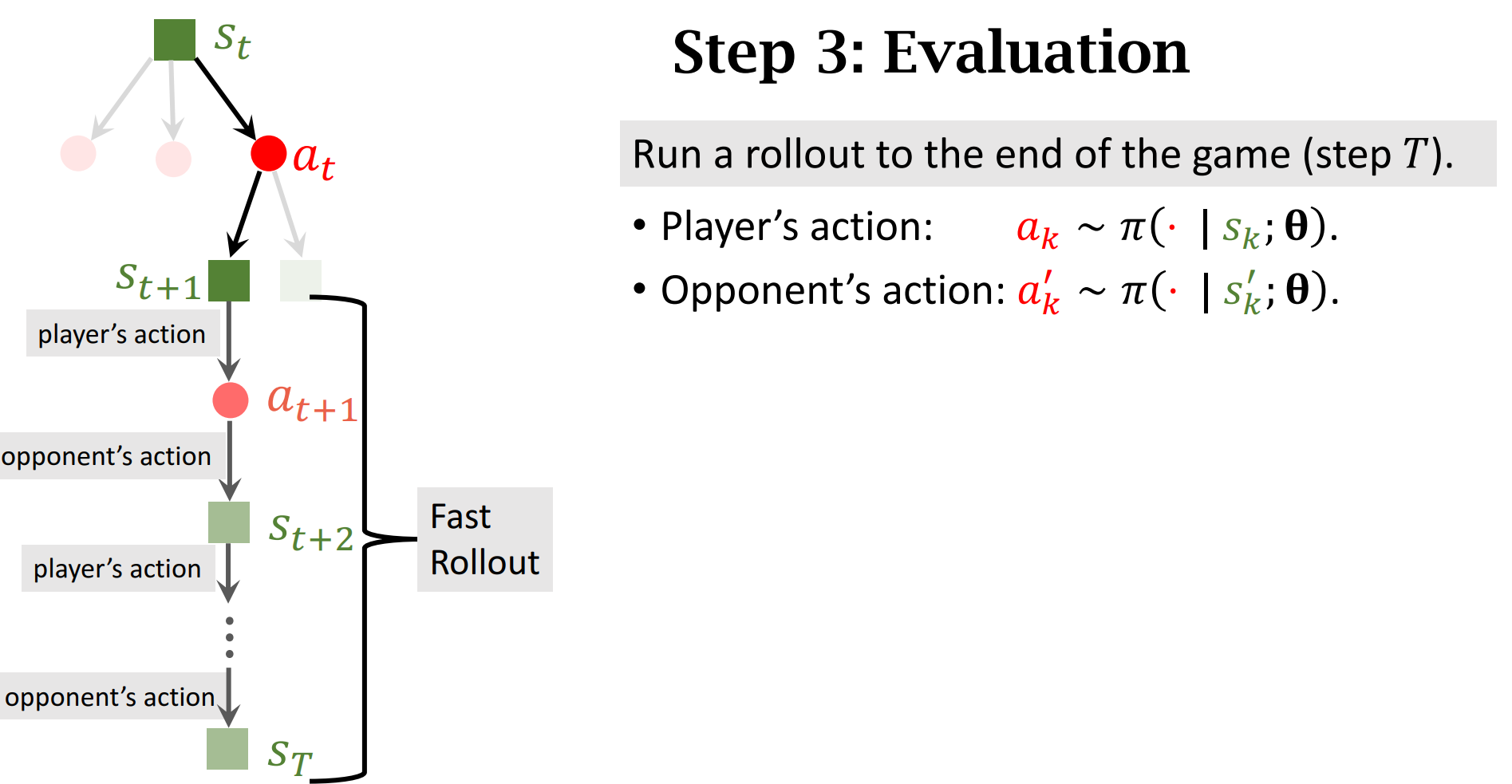
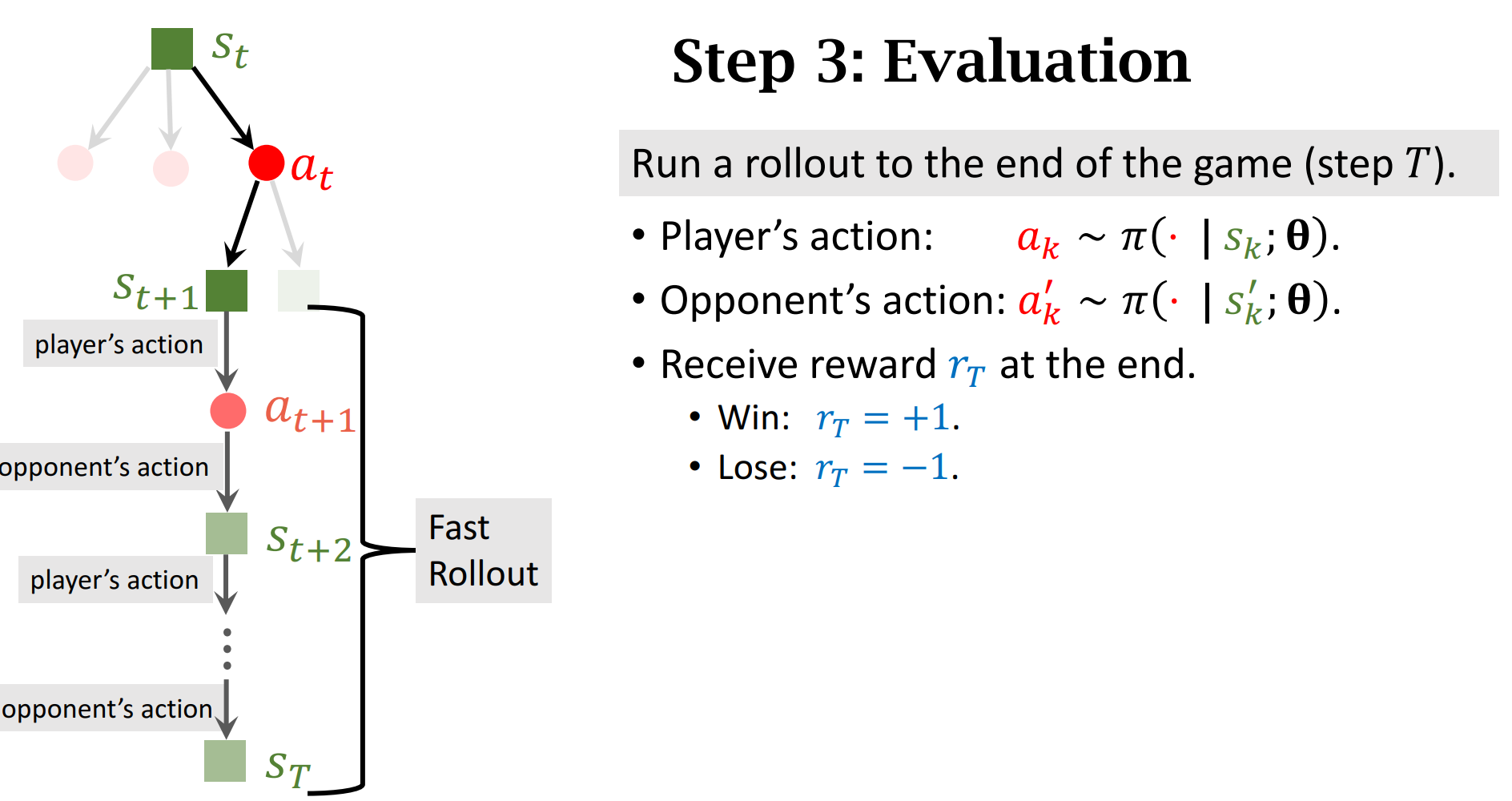




一开始$Q(a)$为零,所以$score$的分数主要取决于$\pi(|)$,之后随着搜索次数的增加,$N(a)$增大,第二项变小,$score$的分数主要取决于$Q(a)$

经过许多次搜索迭代之后
$Q(a)$值和$\pi$ 越大,访问次数$N(a)$值就会越大

Summary Of MCTS$\P$

Summary of AlphaGo

AlphaGo Zero v.s. AlphaGo
旧版MCTS 是模仿人类玩家,而新版MCTS是模仿自己搜索

仿真环境behavior可能是无用的,实际环境下behavior是有用的(不然代价太大)

新版在train时就用了MCTS,用策略网络预测P,用MCTS预测n,我们应该让p接近n才行,因为搜索得到的结果是比较靠谱的,我们用梯度下降来更新策略网络以此修正


Monte Carlo Algorithms
蒙特卡罗方法(Monte Carlo method),也称 统计模拟方法
蒙特卡洛方法的理论基础是大数定律。大数定律是描述相当多次数重复试验的结果的定律,在大数定理的保证下:
利用事件发生的 频率 作为事件发生的 概率 的近似值。
所以只要设计一个随机试验,使一个事件的概率与某未知数有关,然后通过重复试验,以频率近似值表示概率,即可求得该未知数的近似值。
样本数量越多,其平均就越趋近于真实值。
此种方法可以求解微分方程,求多重积分,求特征值等。






TD算法



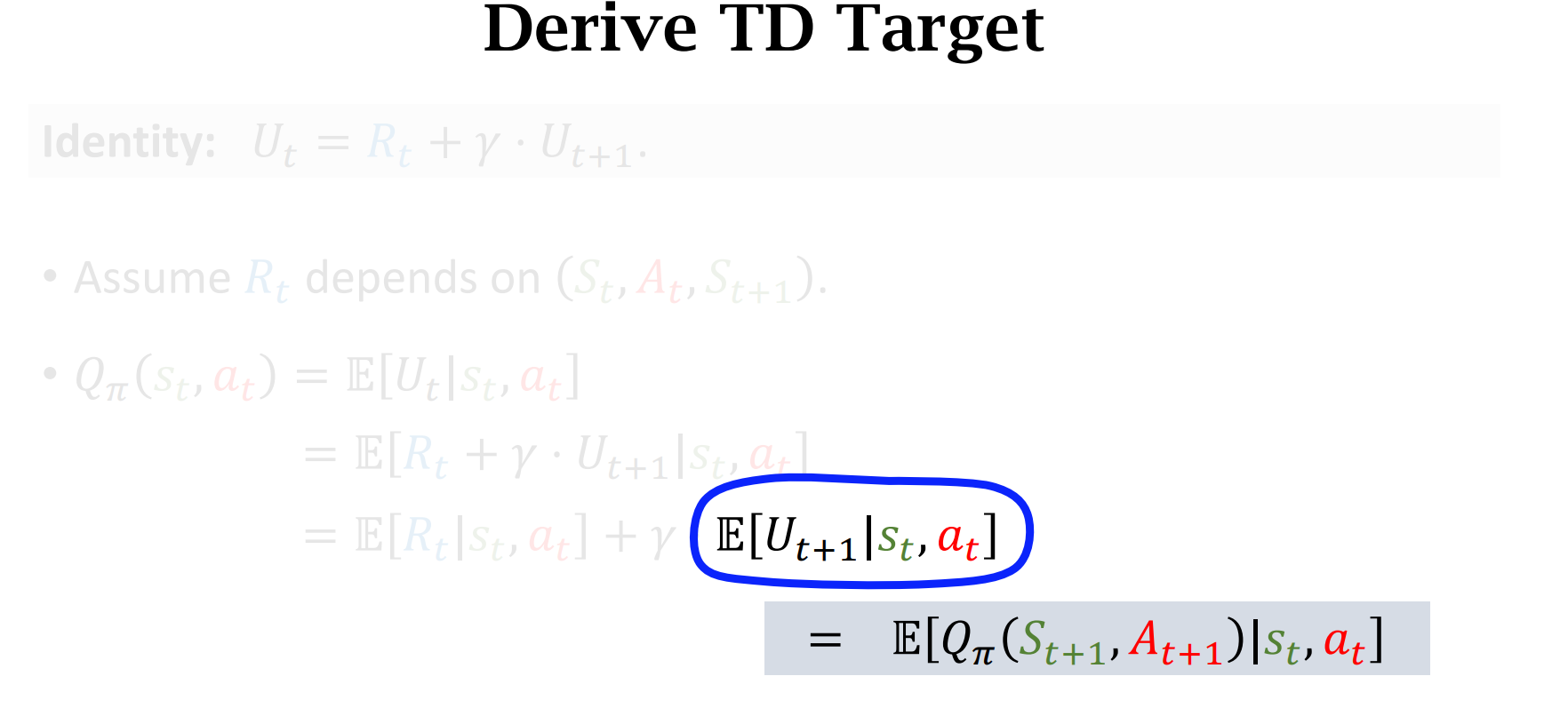

用蒙特卡洛算法近似期望

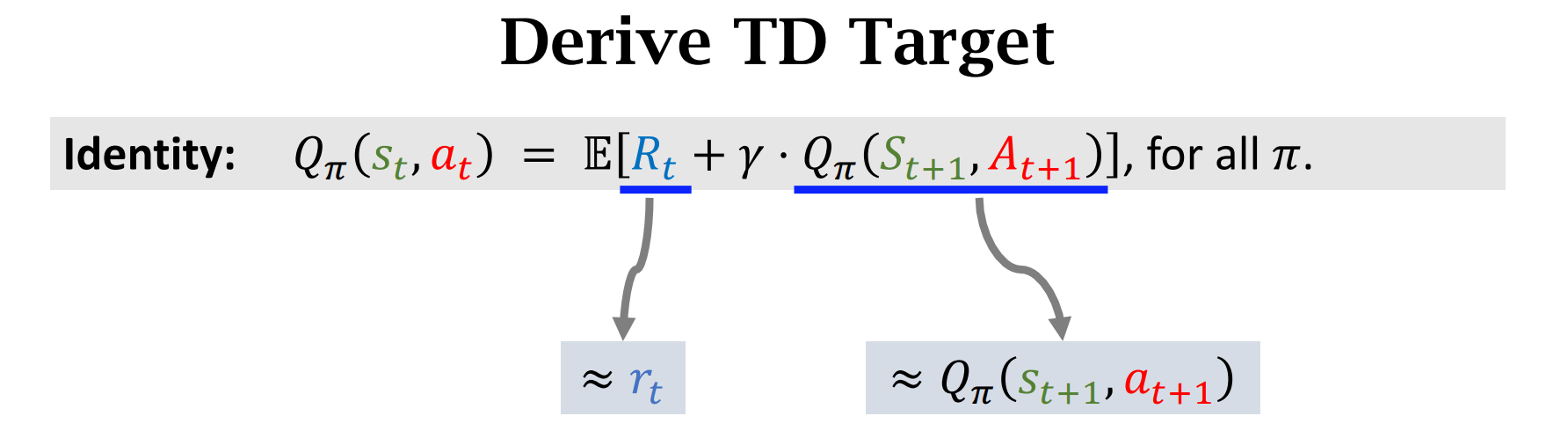

$Q_\pi$是纯估计,蒙特卡洛近似的期望有部分真实值,我们的目标是让$Q_\pi$去接近$y_t$

Sarsa算法






如果$state$和$action$很复杂,那么表格将不在适用,我们用神经网络近似动作价值函数$Q_\pi$
动作价值函数函数$Q$


$Summary$

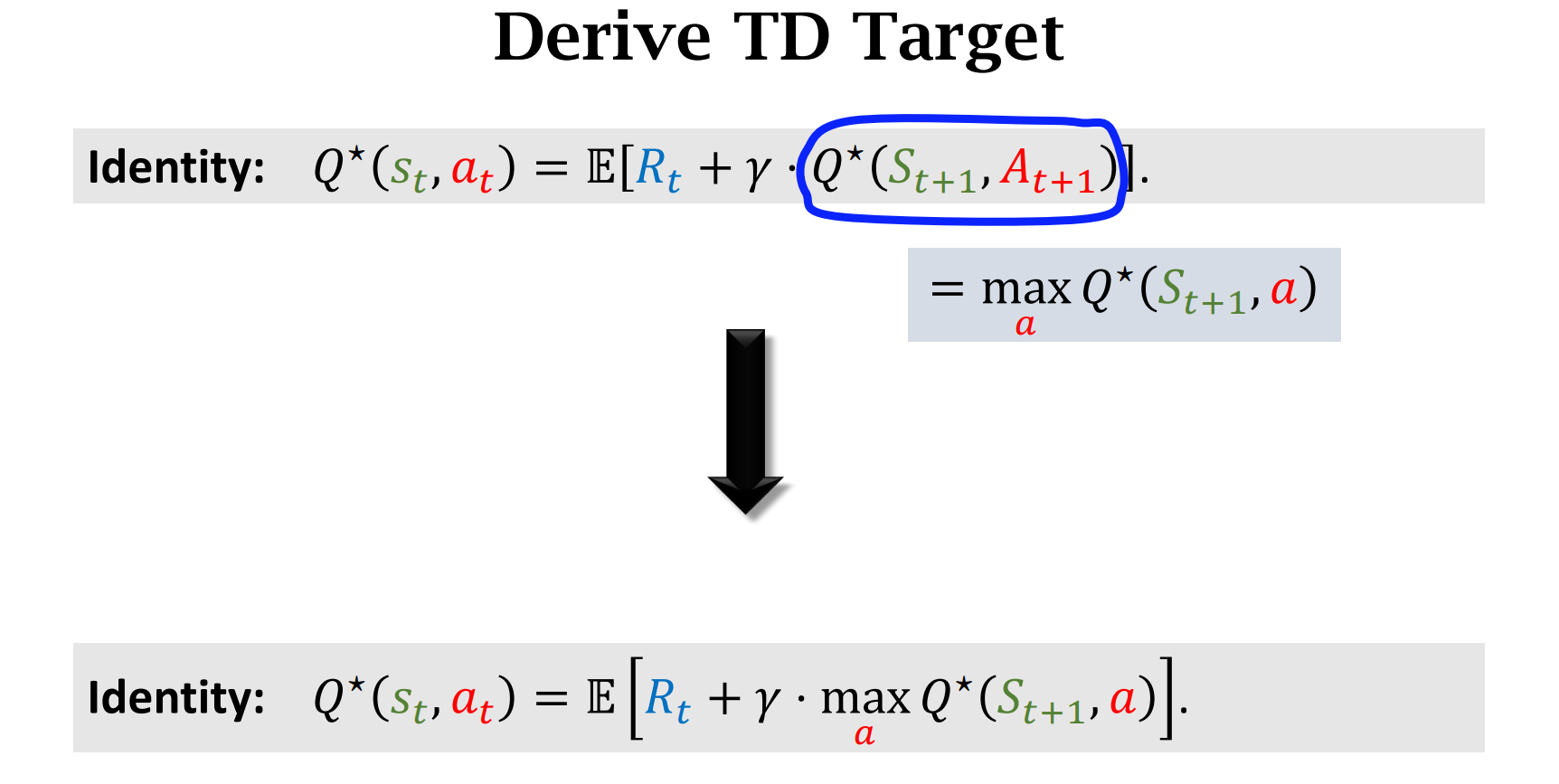
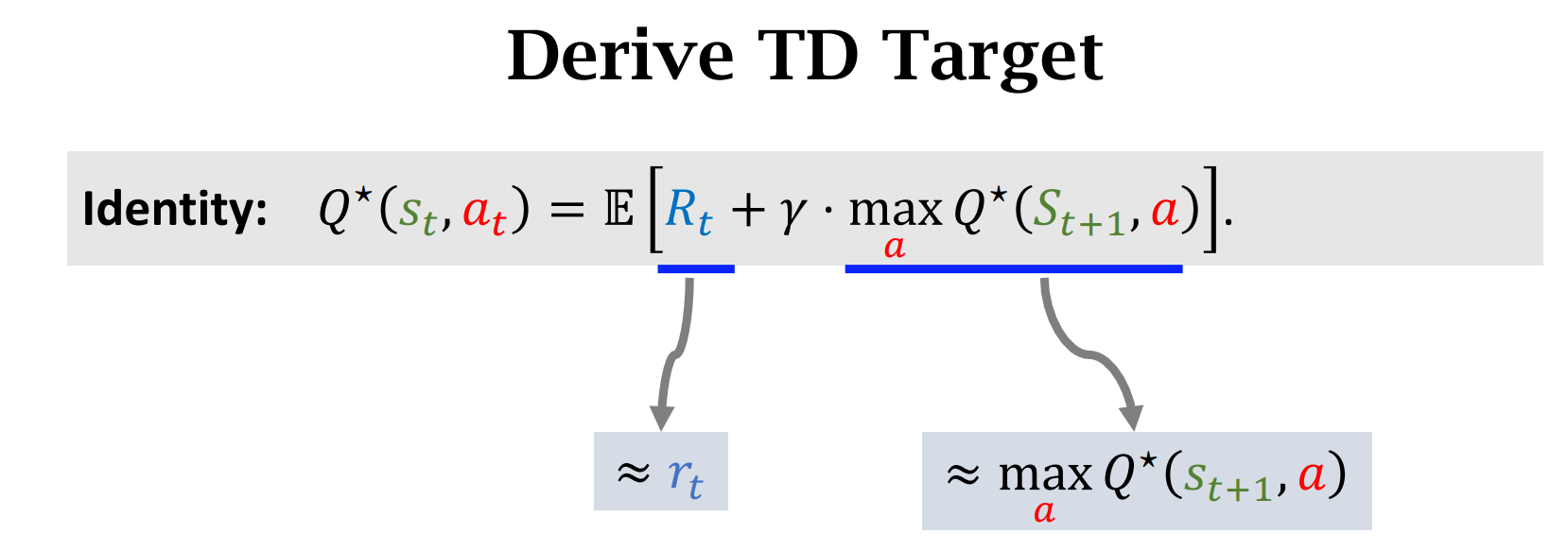
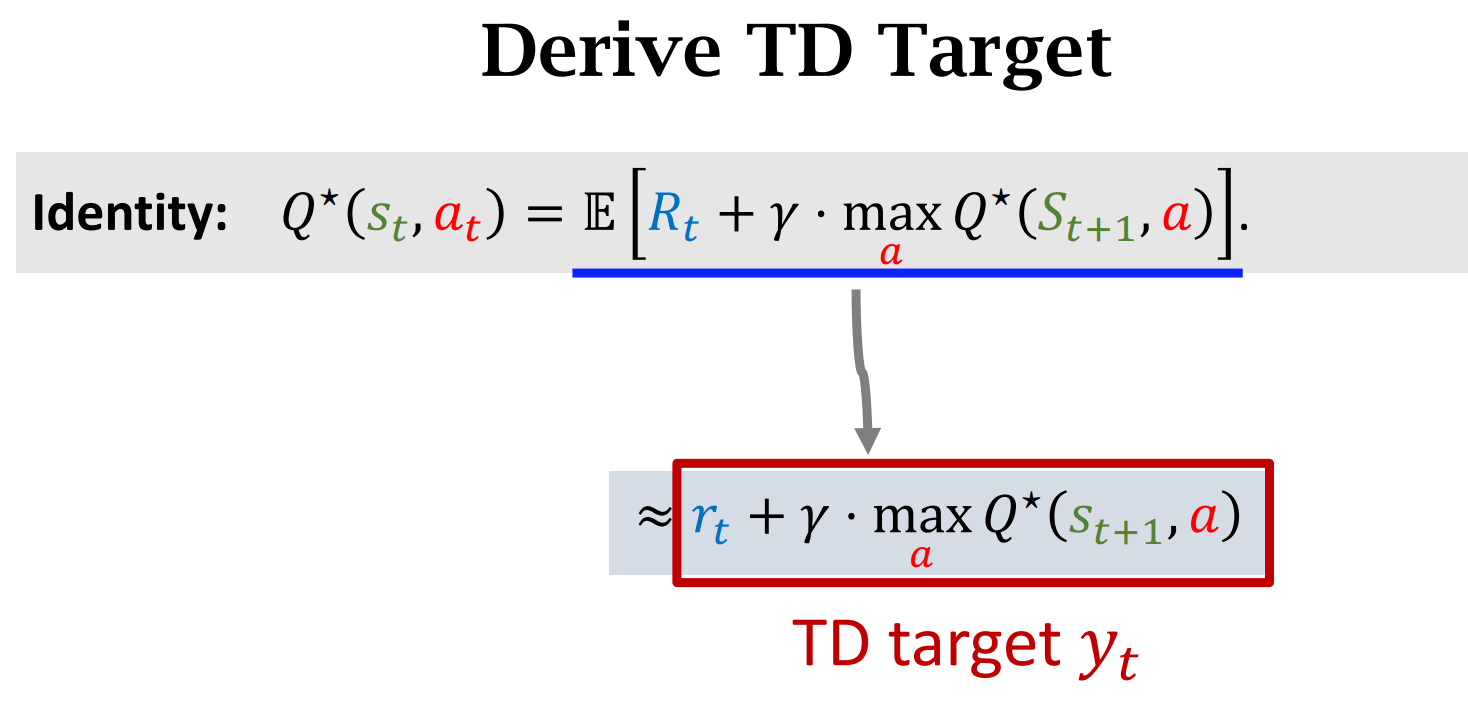
Q-Learning
Sarsa 对应$Q_{\pi}$,Q-learning 对应$Q^*$











$Summary$

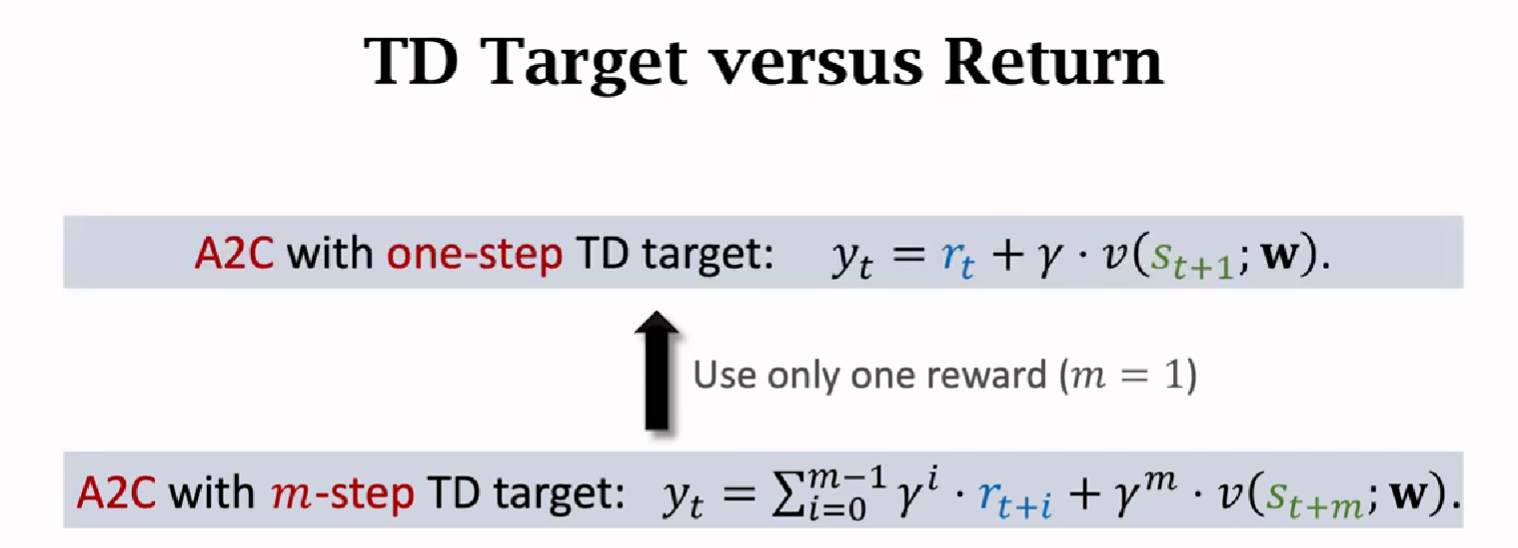
Multi-Step TD Target


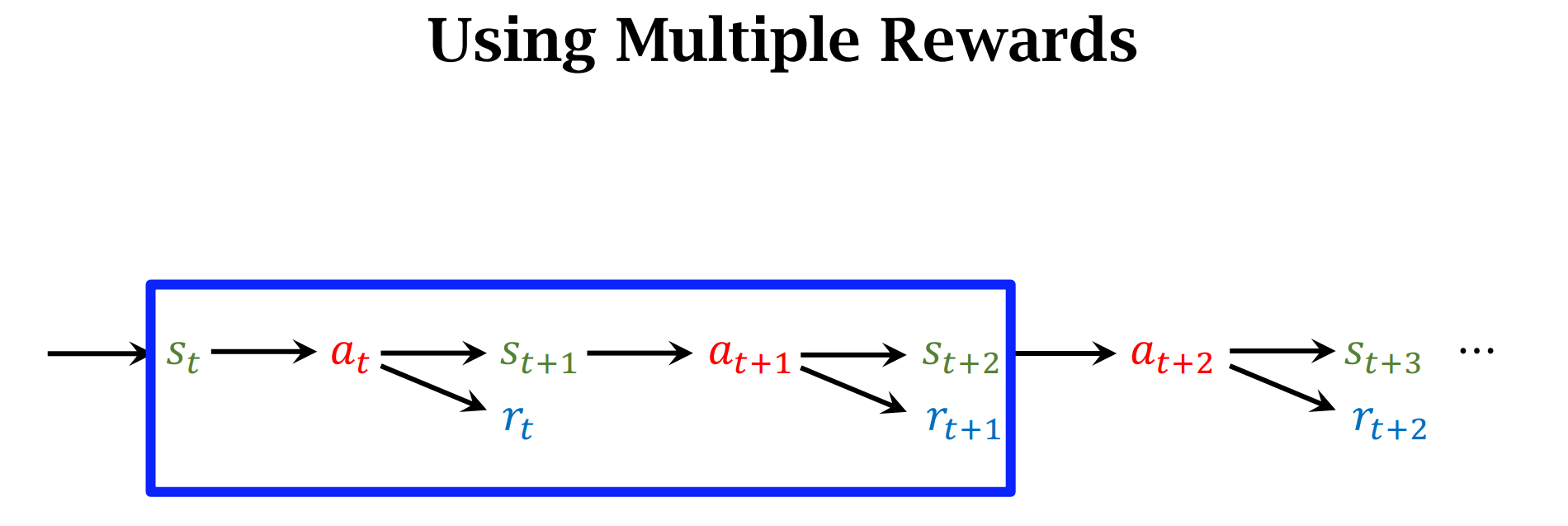






价值函数学习高级技巧
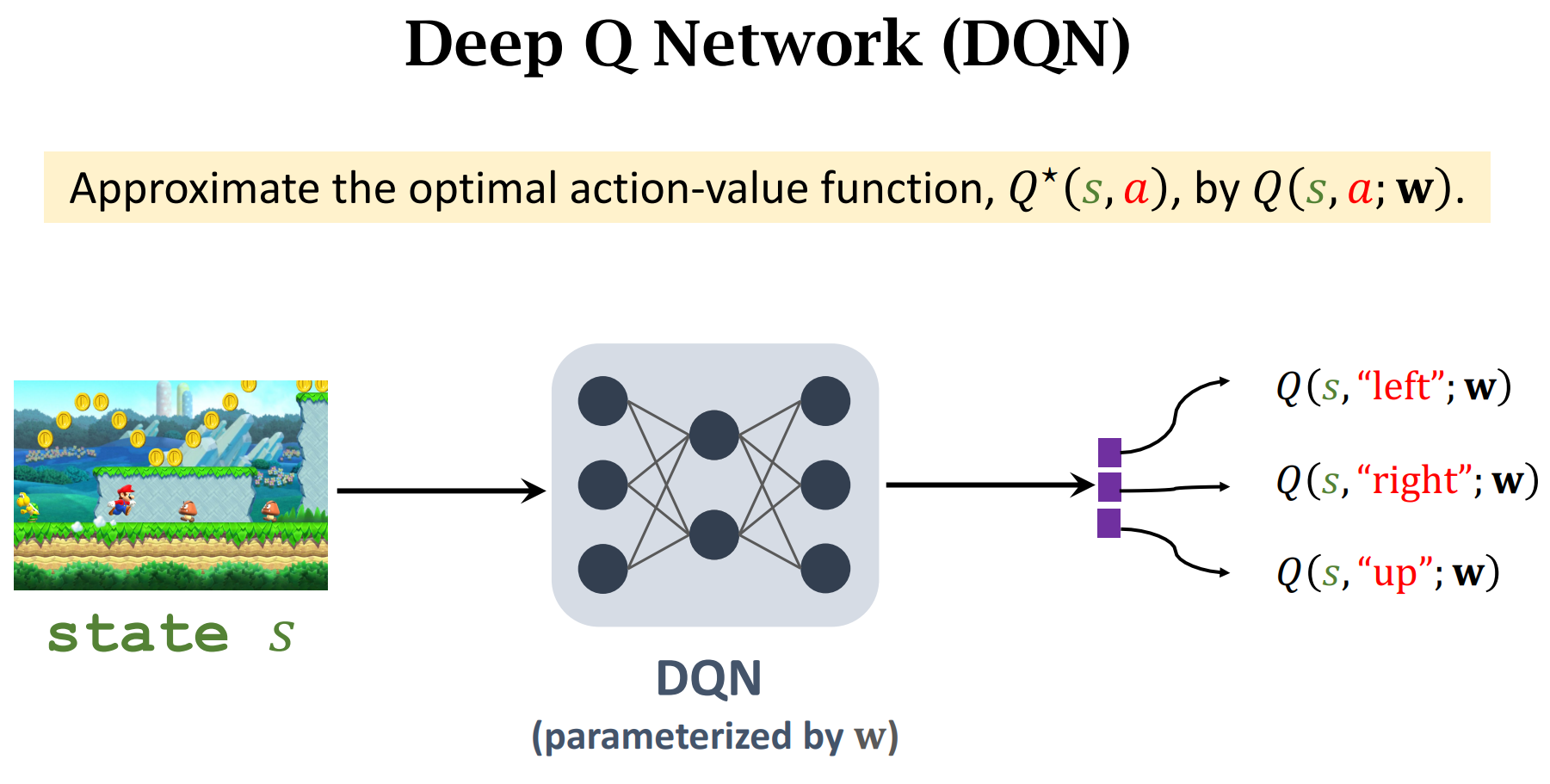



但是,它会有两个主要的缺点


Experience Replay
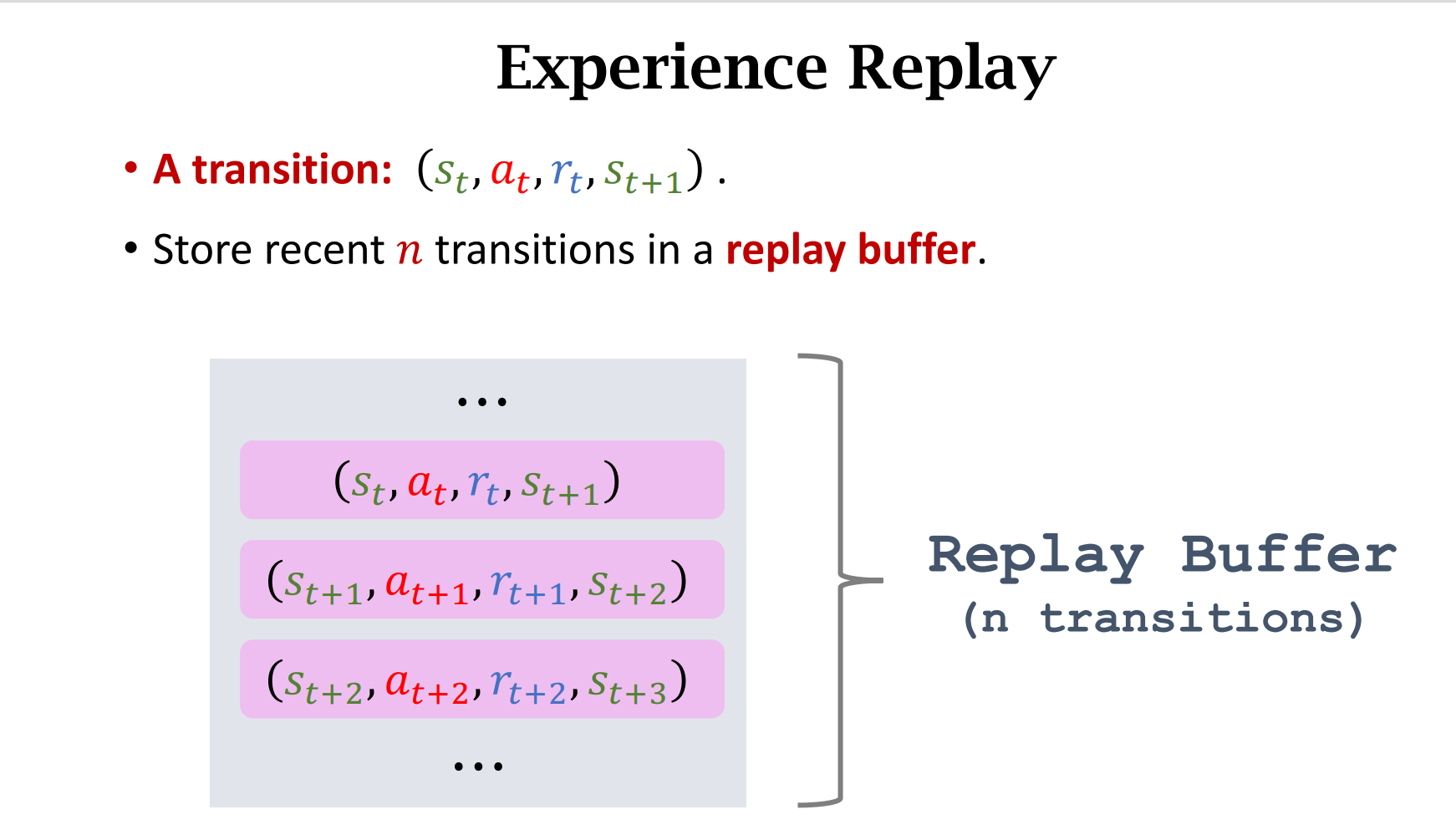




优先经验回放




抽样概率不同,会出现偏差,为了消除偏差我们动态调整学习率

抽样概率越大,学习率应该相应较小;抽样概率越小,学习率应该相应较大



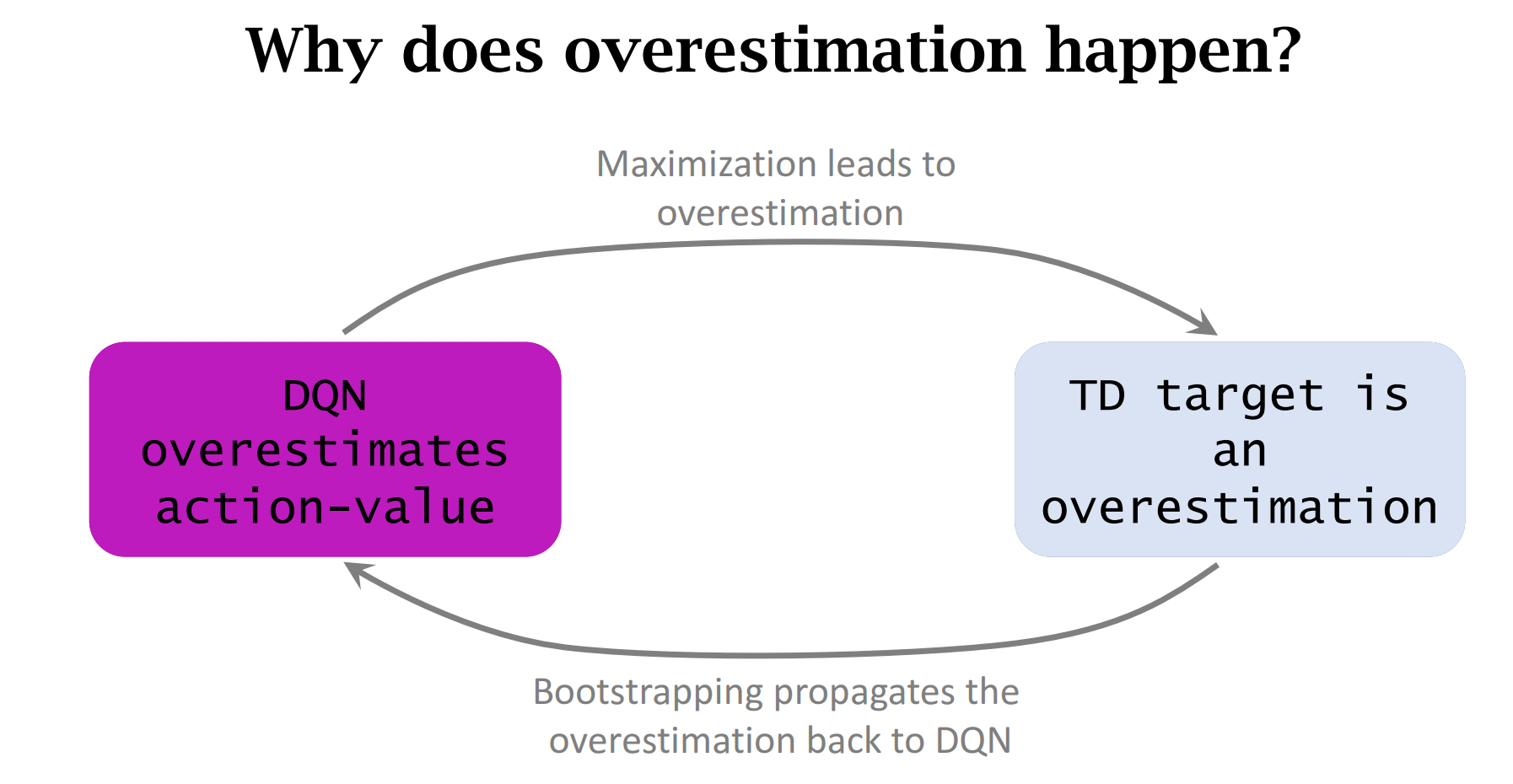
高估问题&解决方法







循环往复,高估现象会加剧







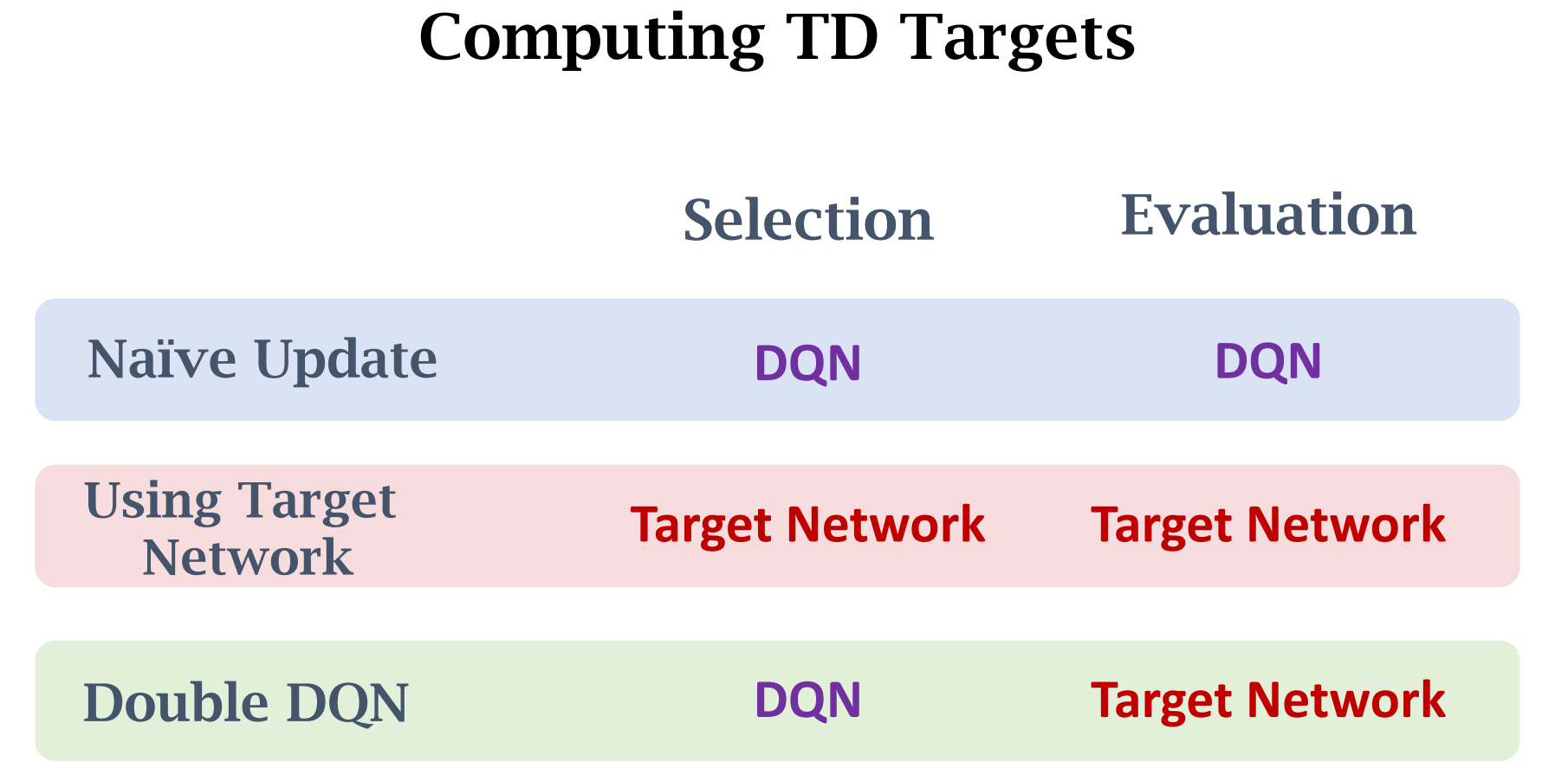
Target Network 无法解决高估问题,只能缓解,因为$W^-$ 与 $W$有关




Double DQN中,$a^*$是在原DQN网络中选出的,而$y_t$是在Target Network中得出的,所以并不是$max\ Q$的问题。但是DQN只是更好的缓解了高估问题,并没有根除。

Summary

Dueling Network
Advantage Function(优势函数)
动作小$a$越好,$A^*$的值越大

两个基本定理
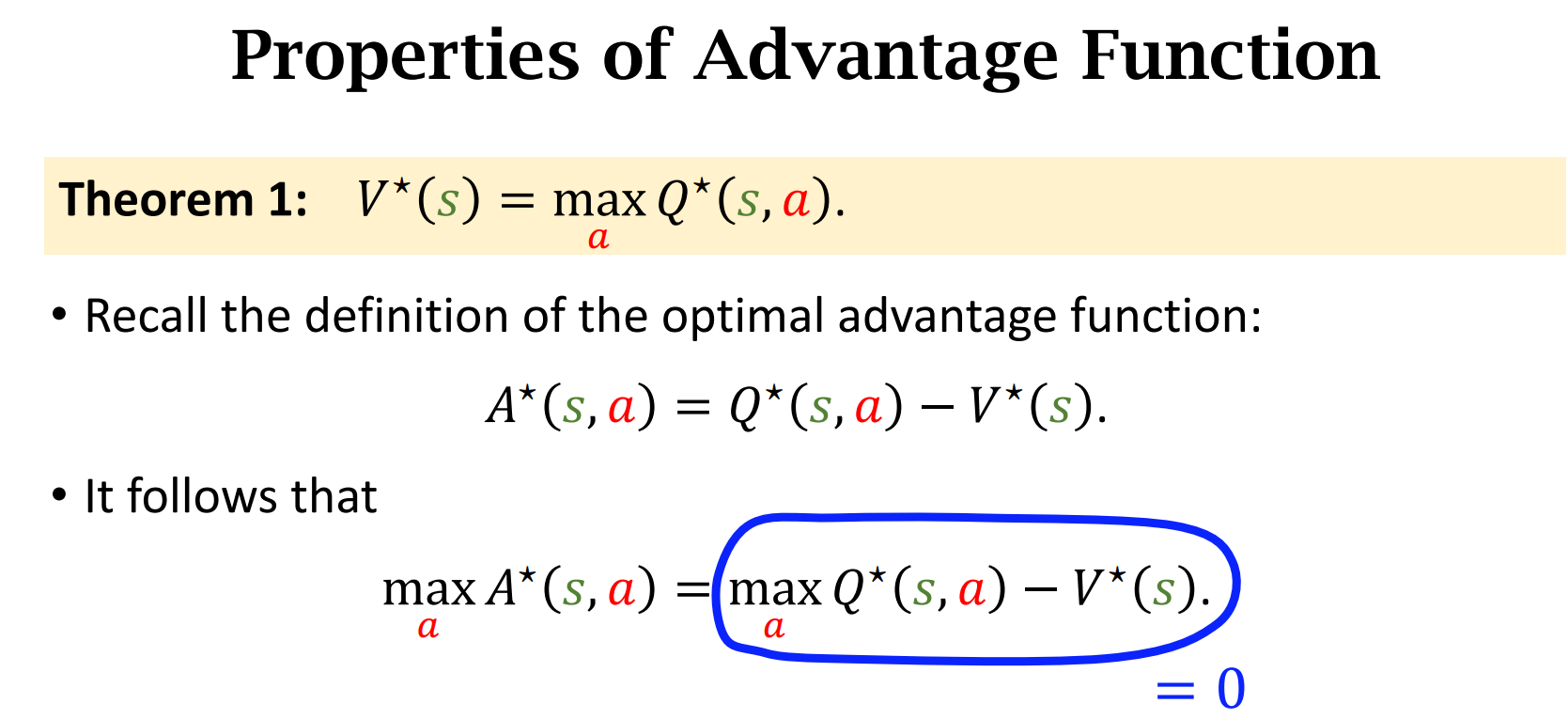
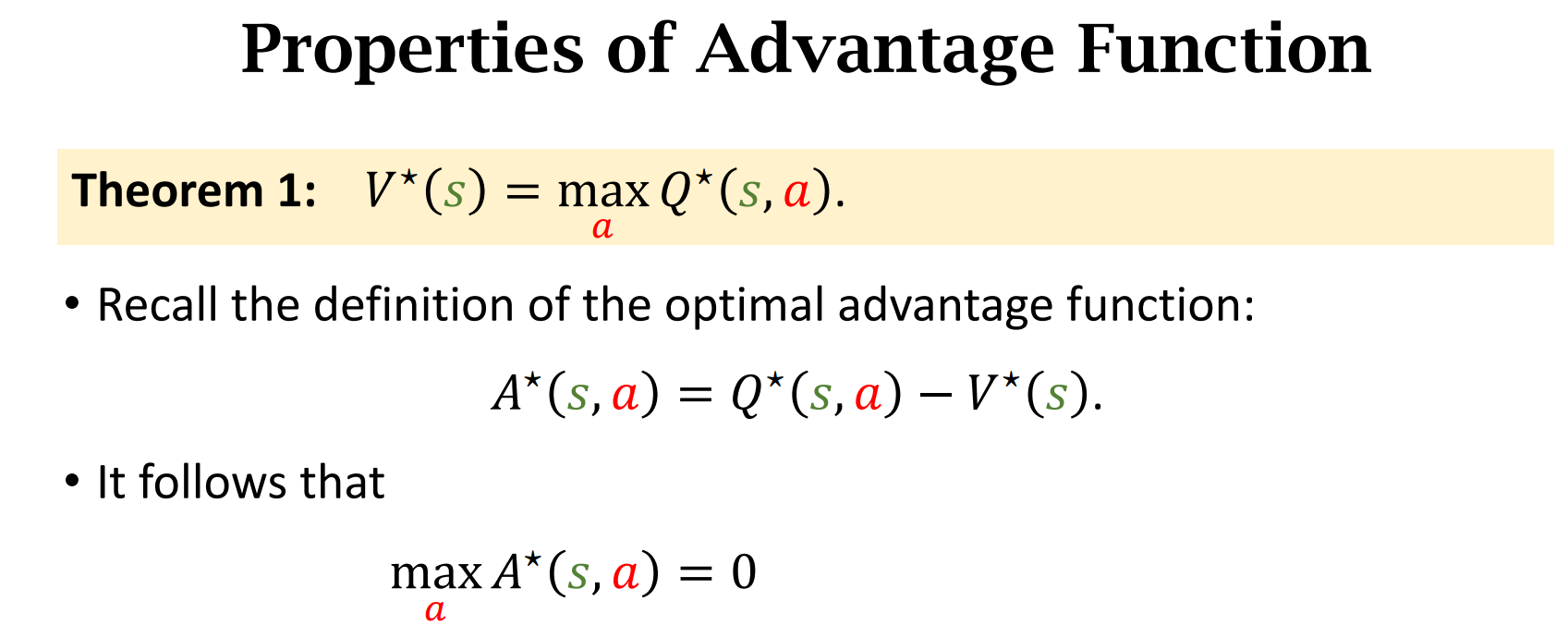



Dueling Network


$A^*$和$V^*$共享卷积层
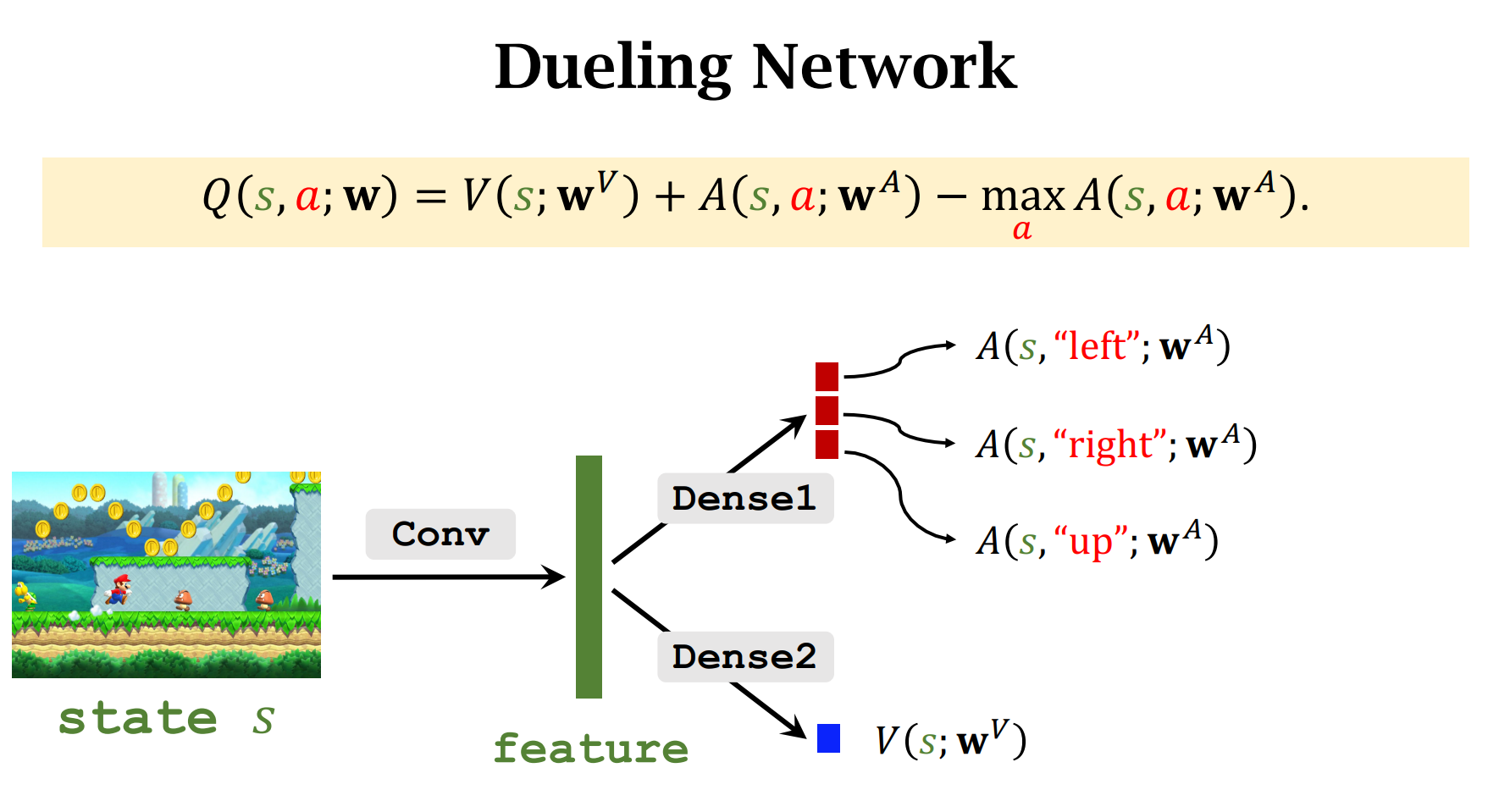
Dueling Network 比DQN结构要好,所以它的表现更好
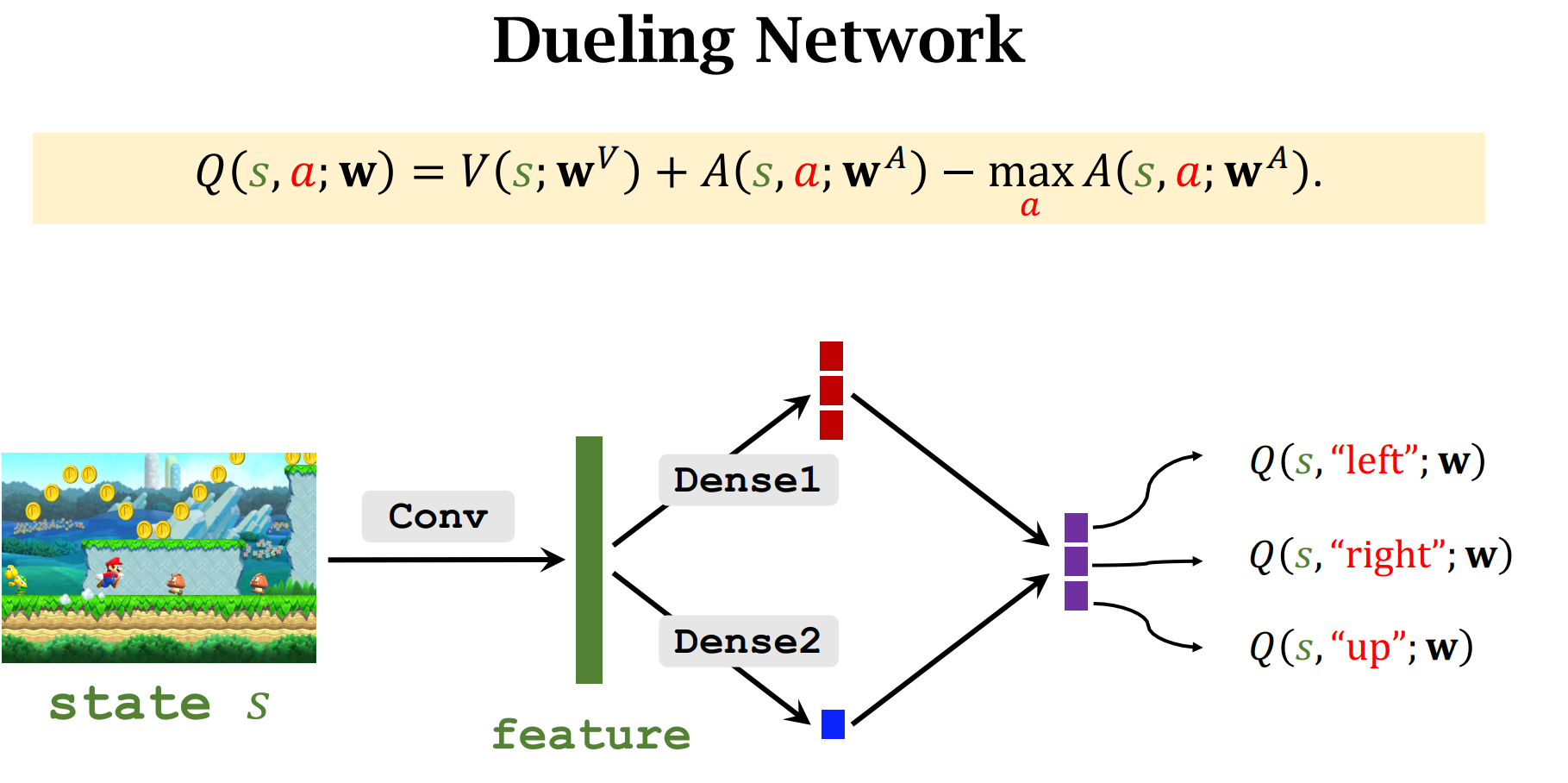
用Q-Learning算法来训练Dueling Network,Dueling Network只是网络结构与DQN不同,训练方法是一样的




在实验中,发现mean的效果哦会更好

在训练时,把V和A看做一个整体,直接训练Q

策略学习
策略梯度中的Baseline

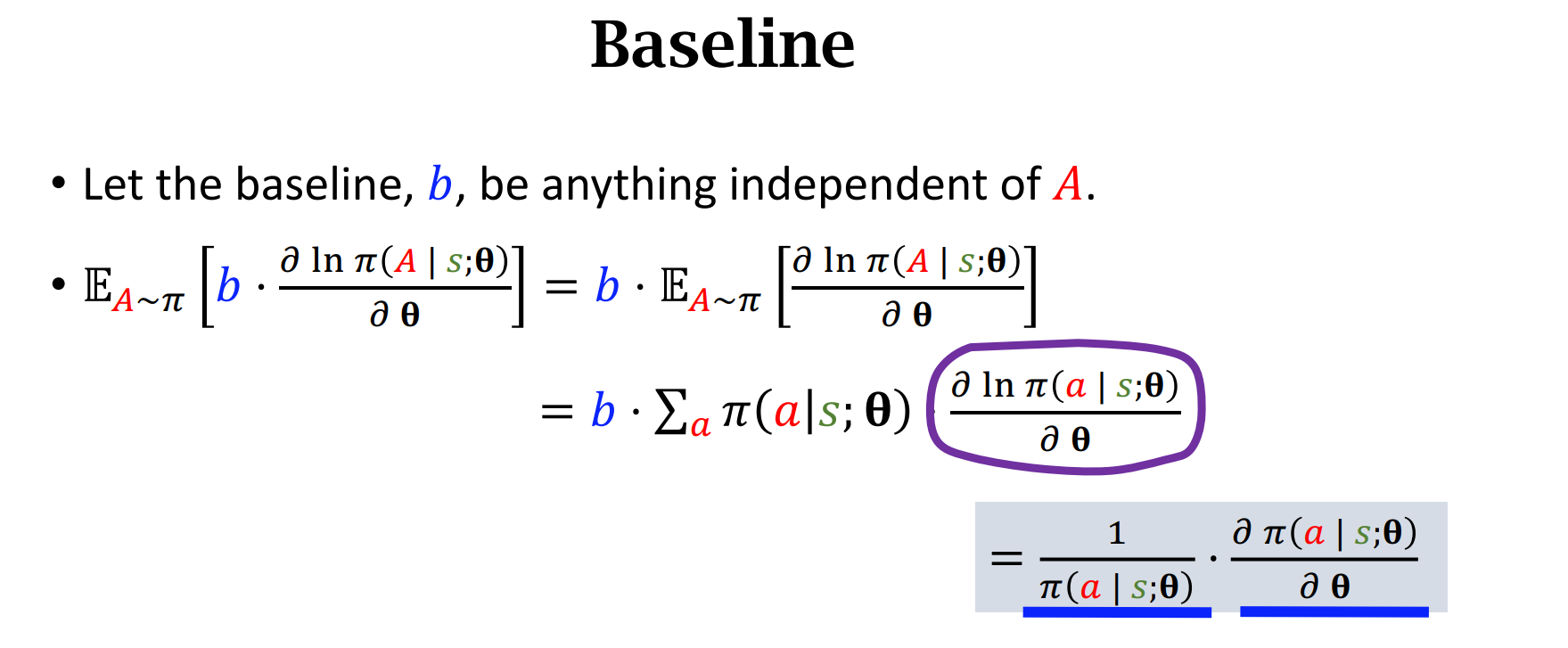









算法中,用蒙特卡洛近似如下公式,虽然$b$不影响如下公式,但是会影响蒙特卡洛近似,如果$b$选择好,近似于$Q_\pi$的话,那么会使得蒙特卡洛的方差降低,算法会收敛更快。

用蒙特卡洛方法近似期望

$g(a_t)$是对策略梯度的蒙特卡洛近似

$\beta$是学习率,$g(a_t)$是随机梯度

$b$不会影响$g(a_t)$的方差,但是会影响$g(a_t)$的数值,如果$b$的选取恰当,那么会降低$g(a_t)$的方差


$v_\pi$是$Q_\pi$的期望,所以是比较接近$Q_\pi$的

Reinforce With Baseline
目标:用Reinforce算法训练策略网络,同时训练价值网络作为Baseline起辅助作用








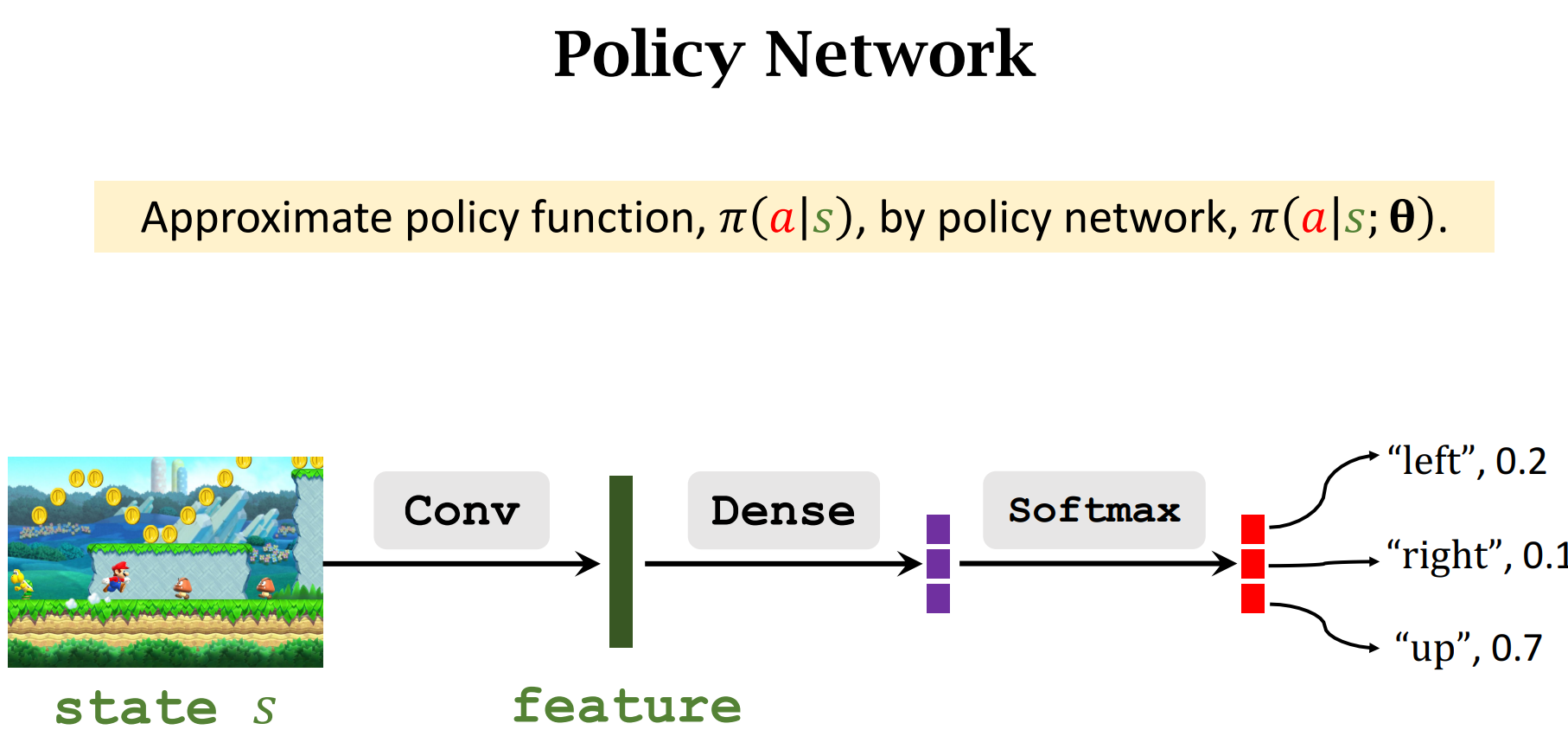
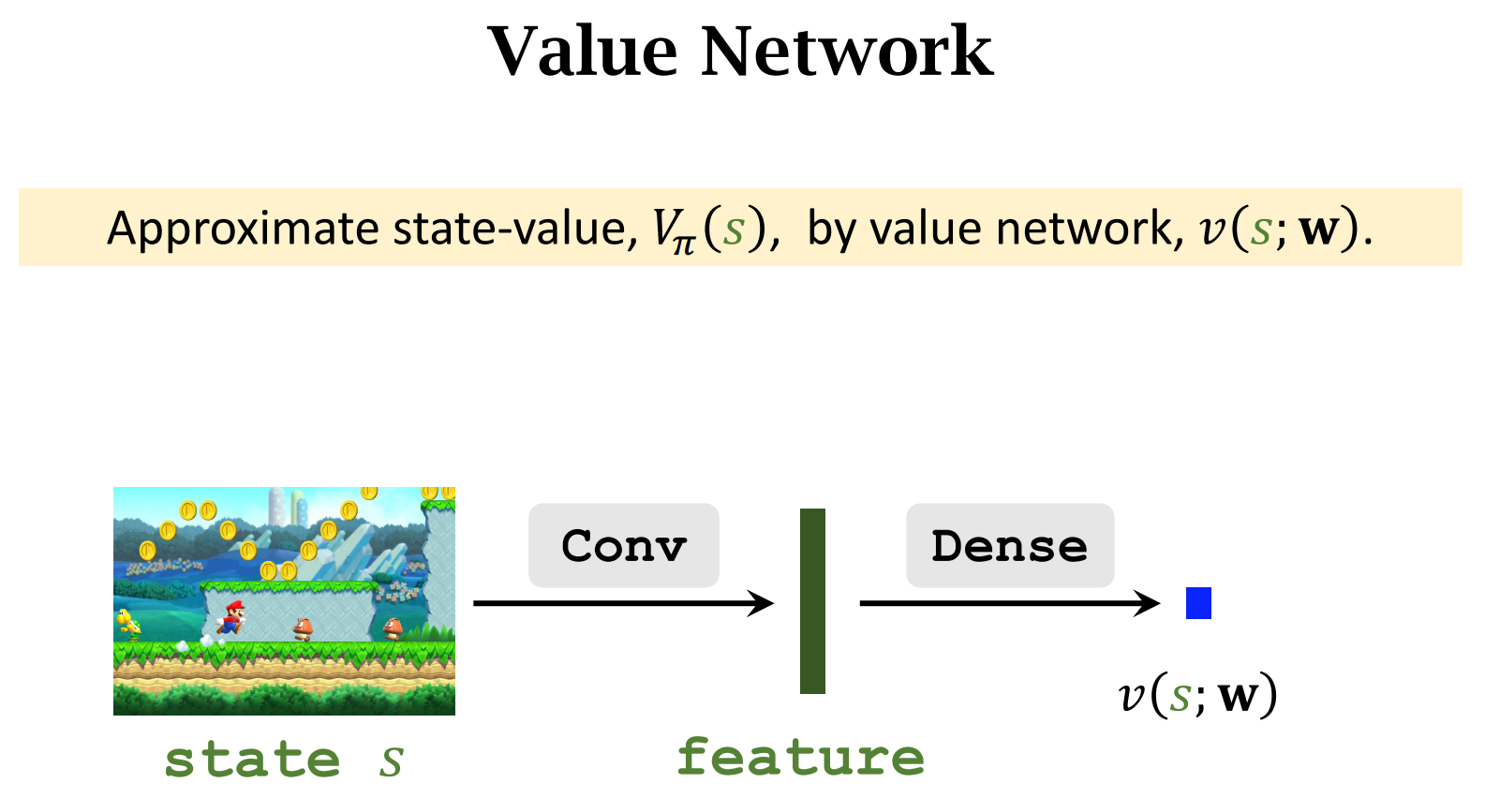
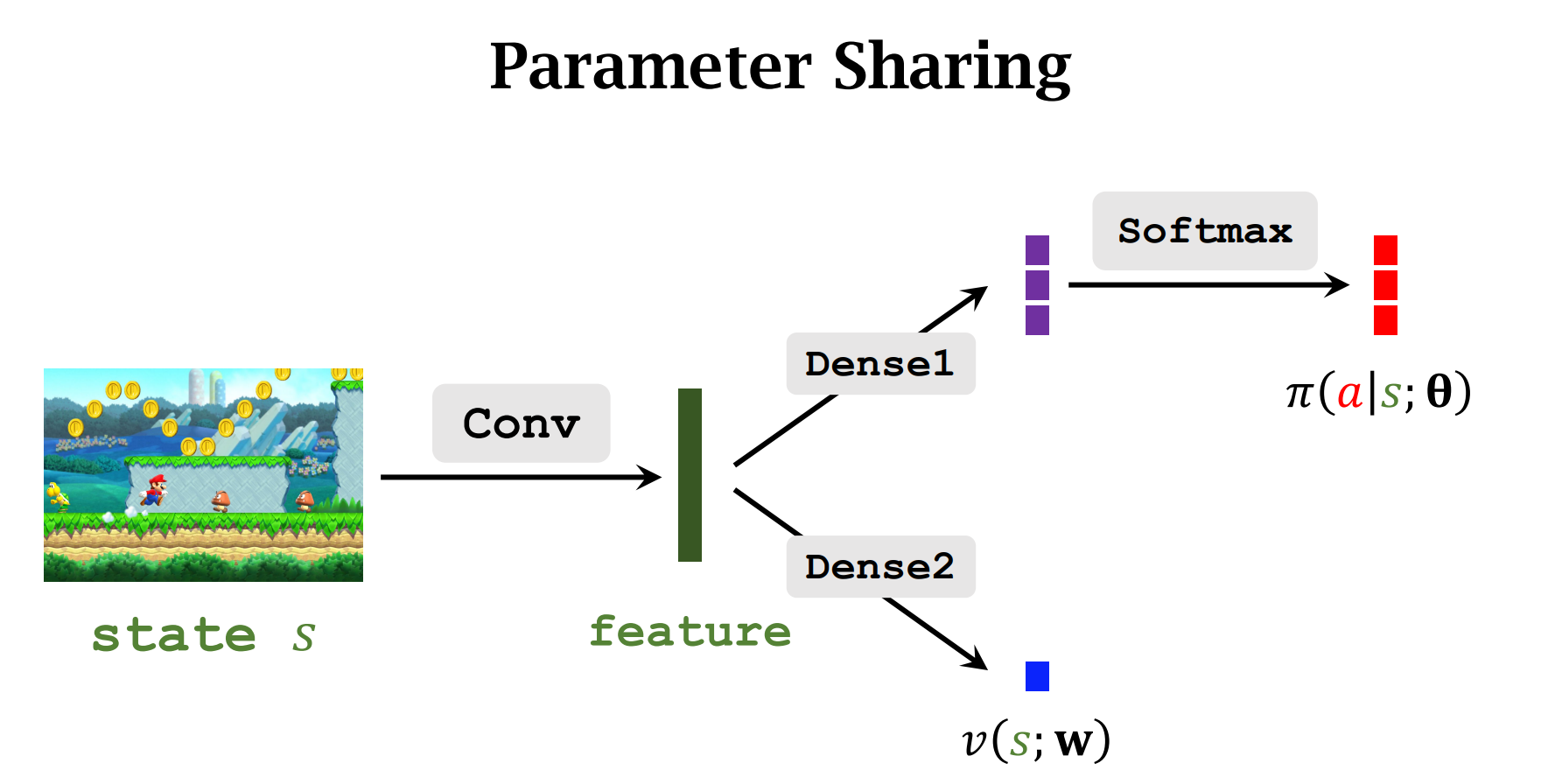




A2C 方法
与AC算法不同的是,AC算法中Critic用的是动作价值函数Q,而A2C方法中用的是状态价值函数V,比Q好训练(Q依赖于S和A,V只依赖于S)

也是用到了两个神经网络,结构和上个算法相似
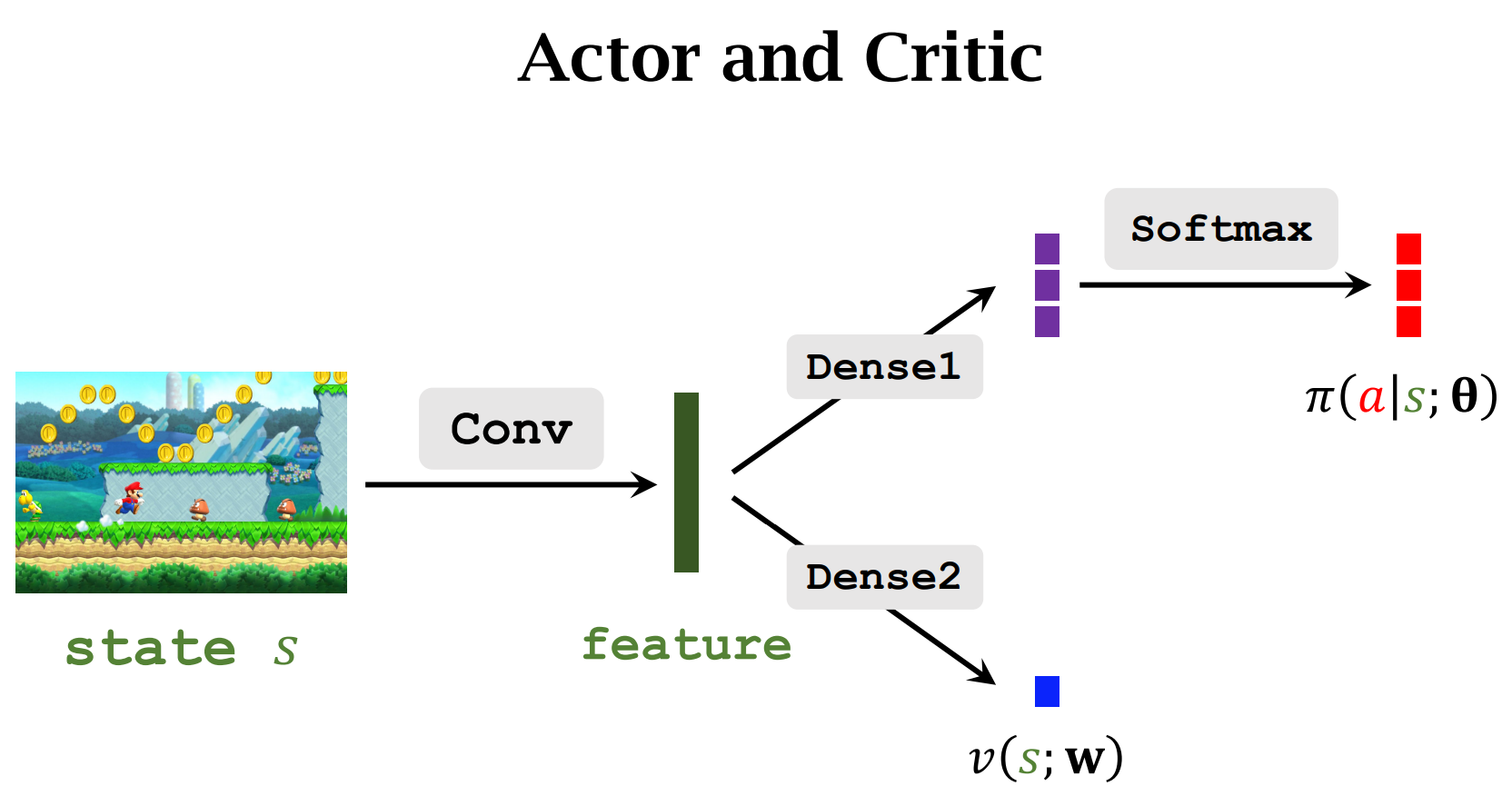
训练方法

数学推导

Reinforce 与 A2C的区别
神经网络结构一样
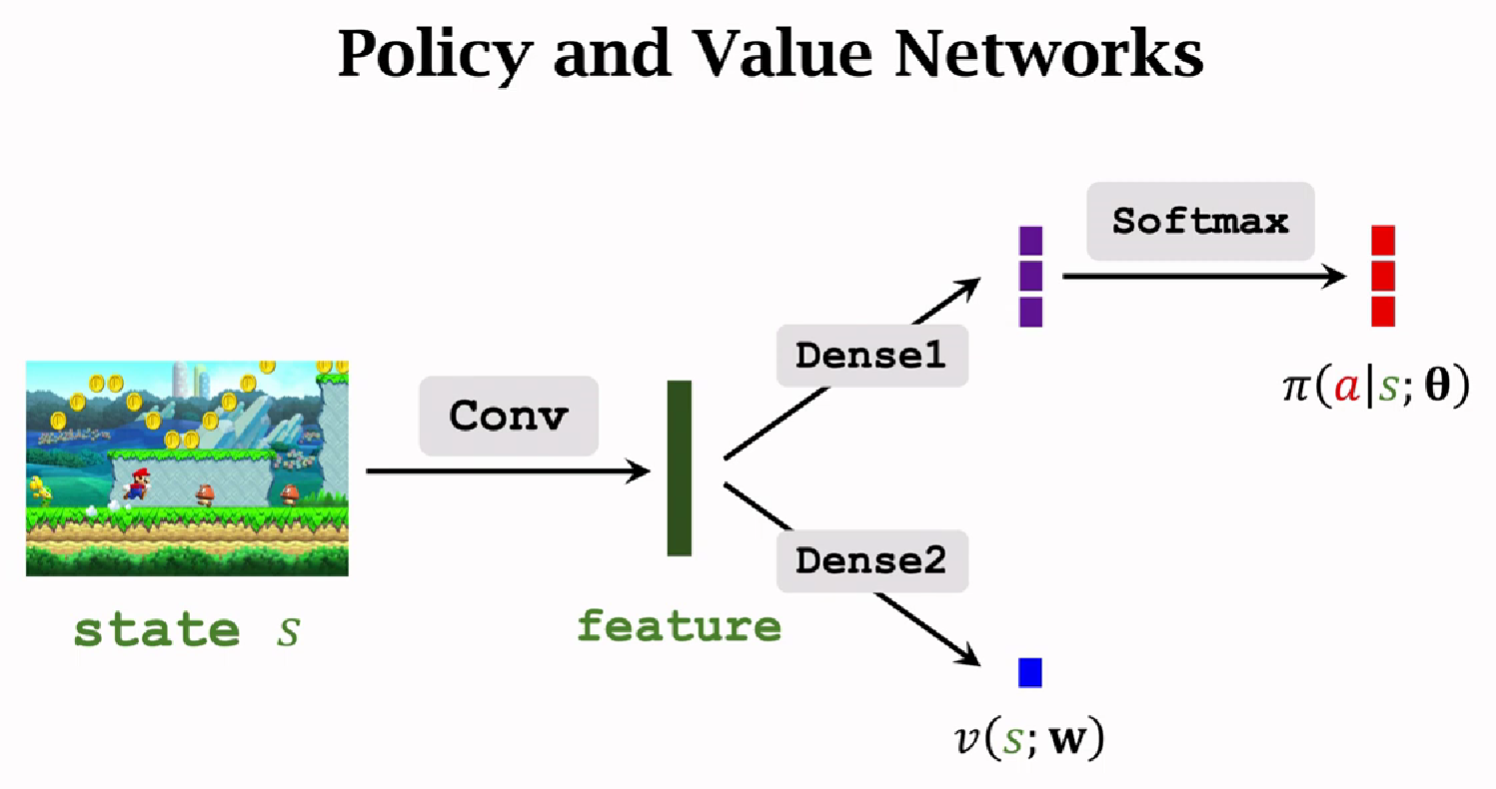
区别1:
价值网络v的用途不一样。



A2C用的是$y_t$,而Reinforce用的是真实奖励$u_t$

A2C versus Reinforce
Reinforce 是A2C的一种特例

离散控制与连续控制


对连续控制的处理1——离散化,适用于自由度比较小的问题


确定策略梯度
Deterministic Policy Gradient (DPG)
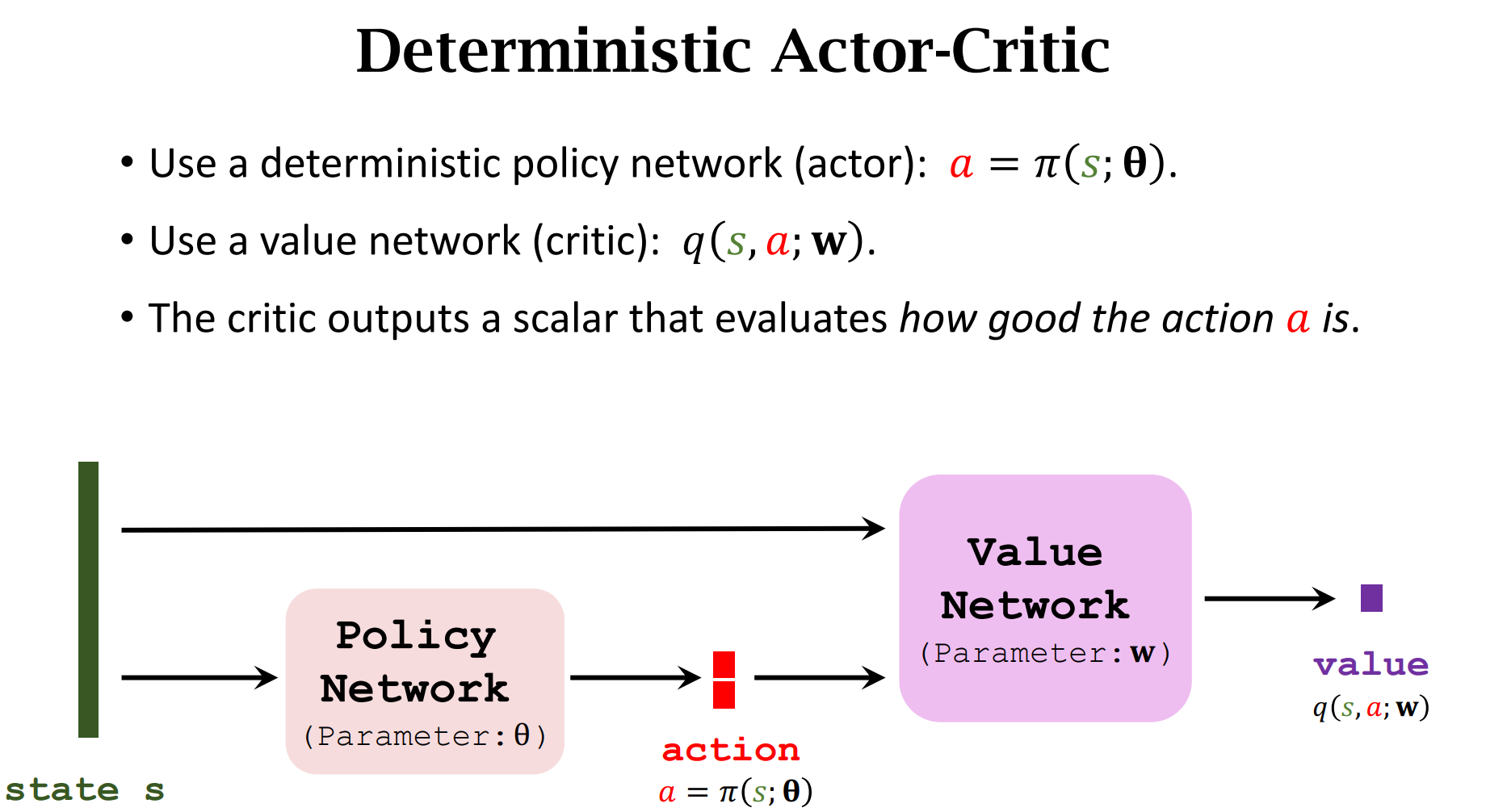


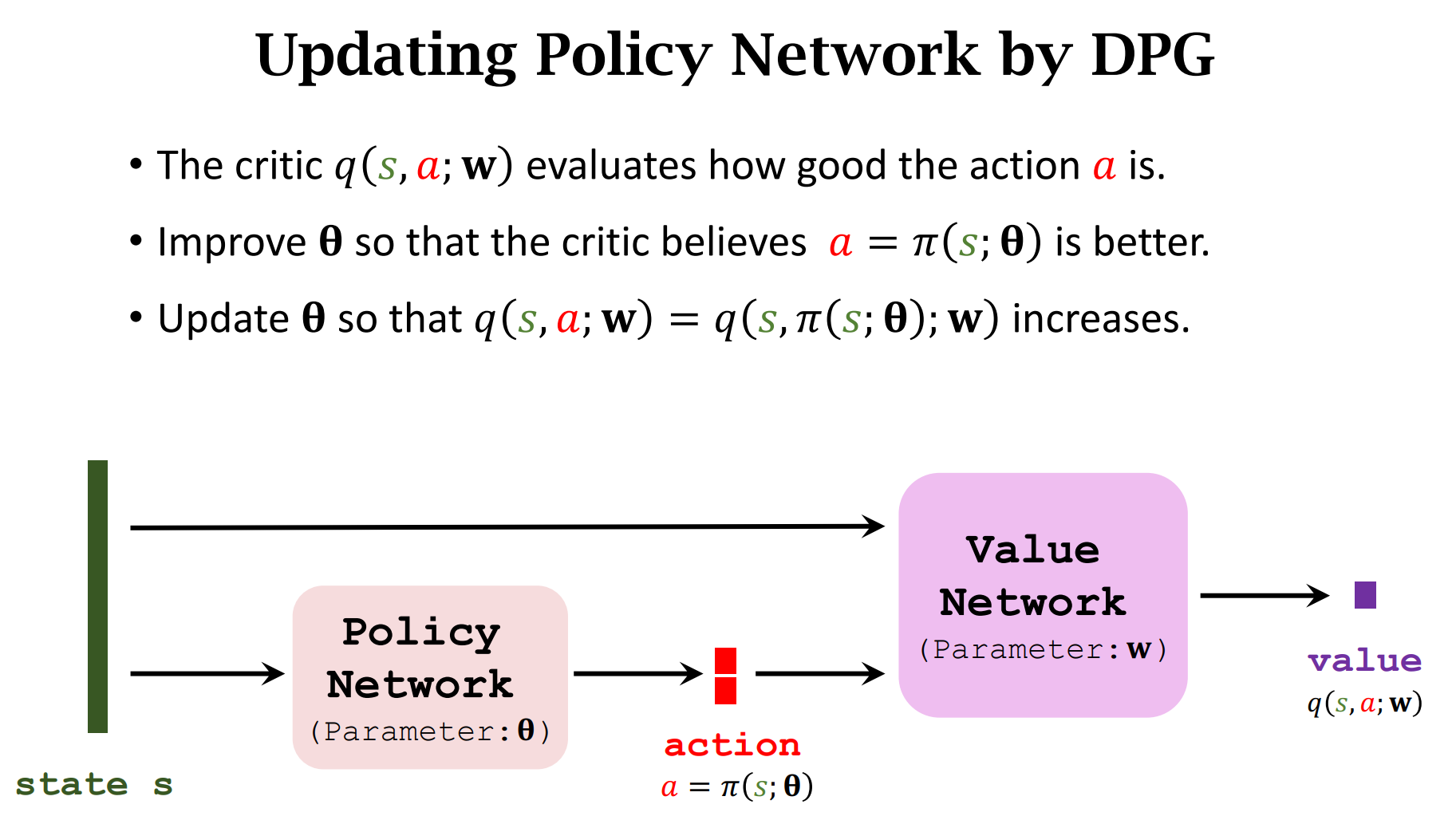
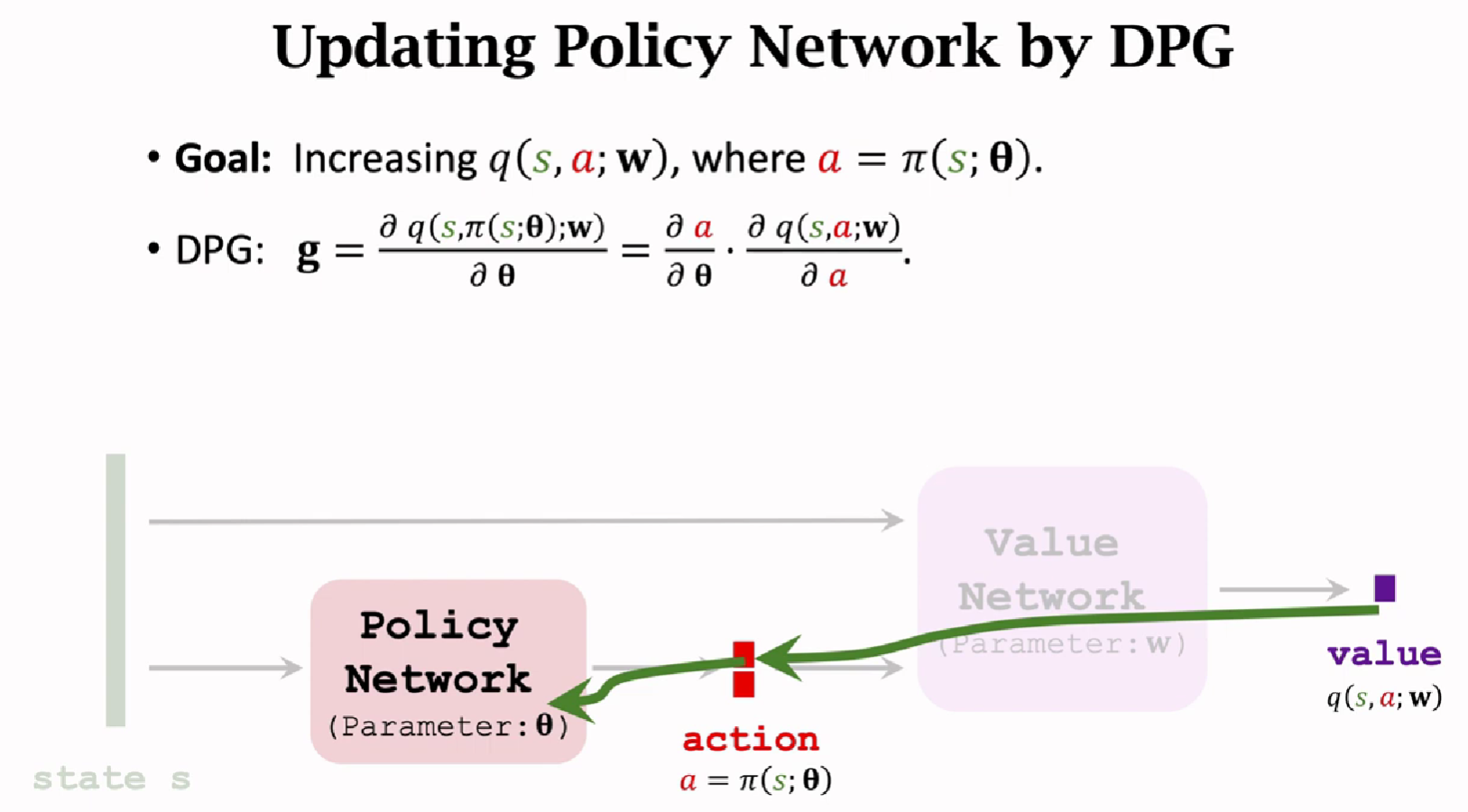
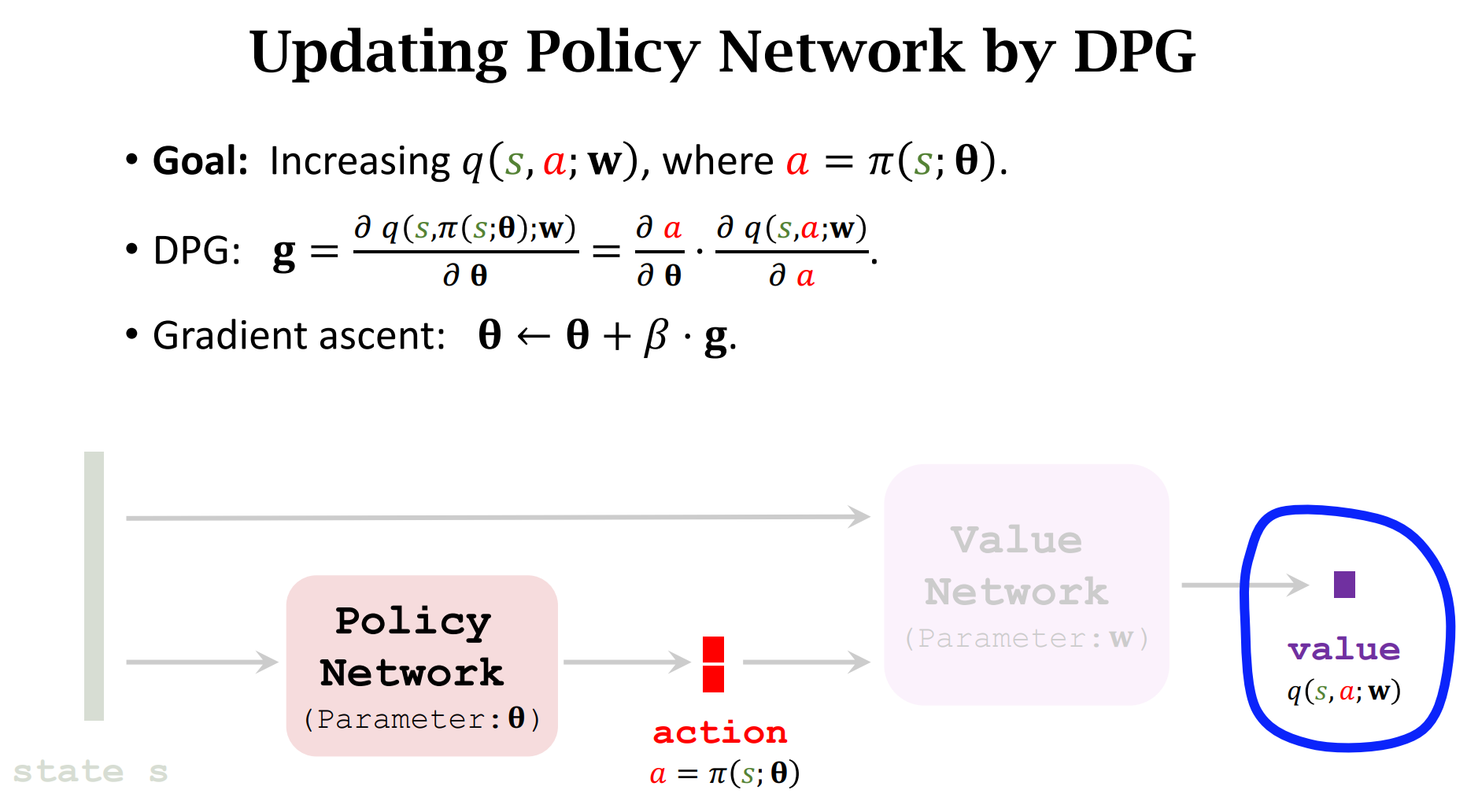

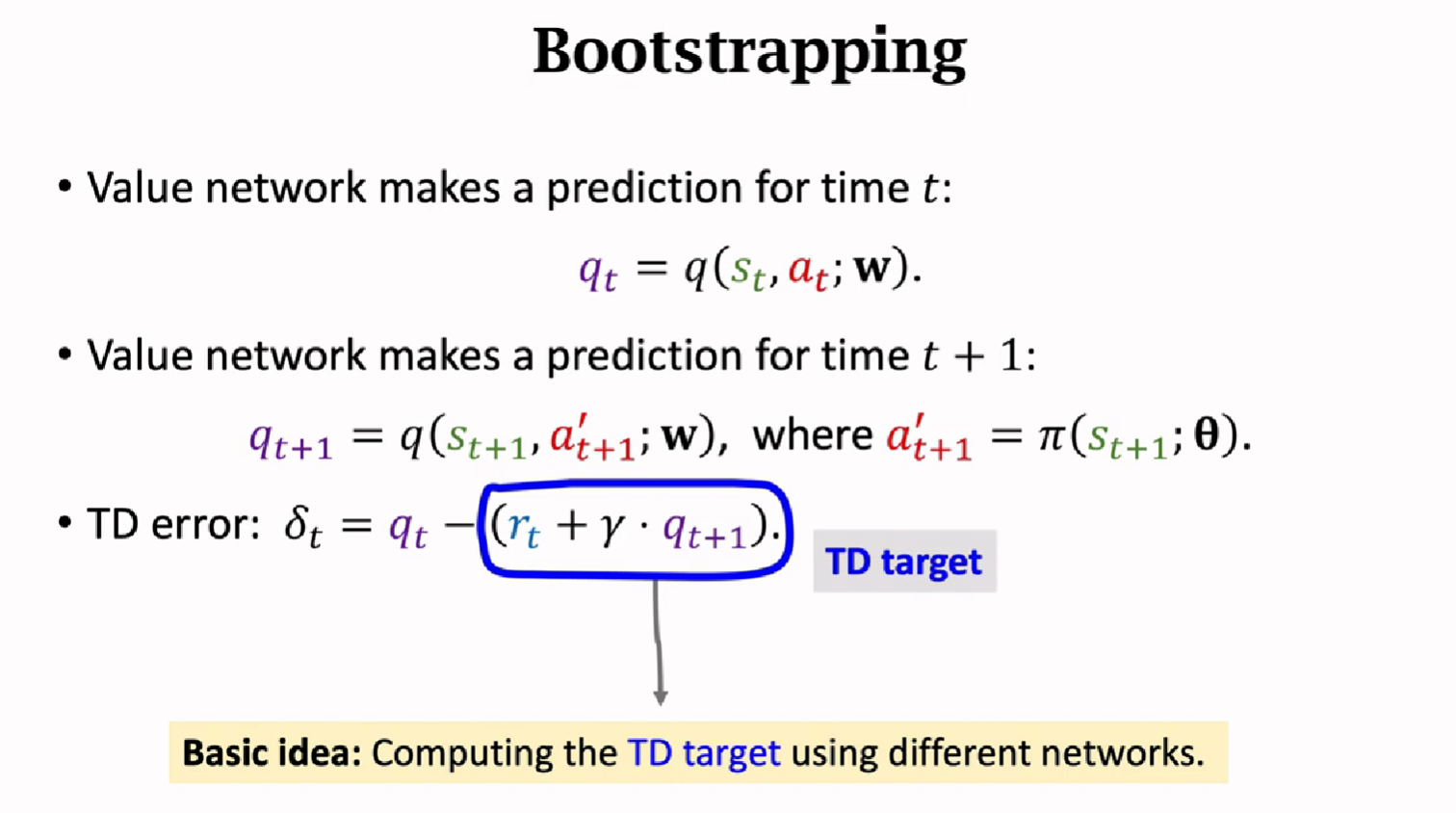





随机策略做连续控制
多智能体强化学习

基本概念











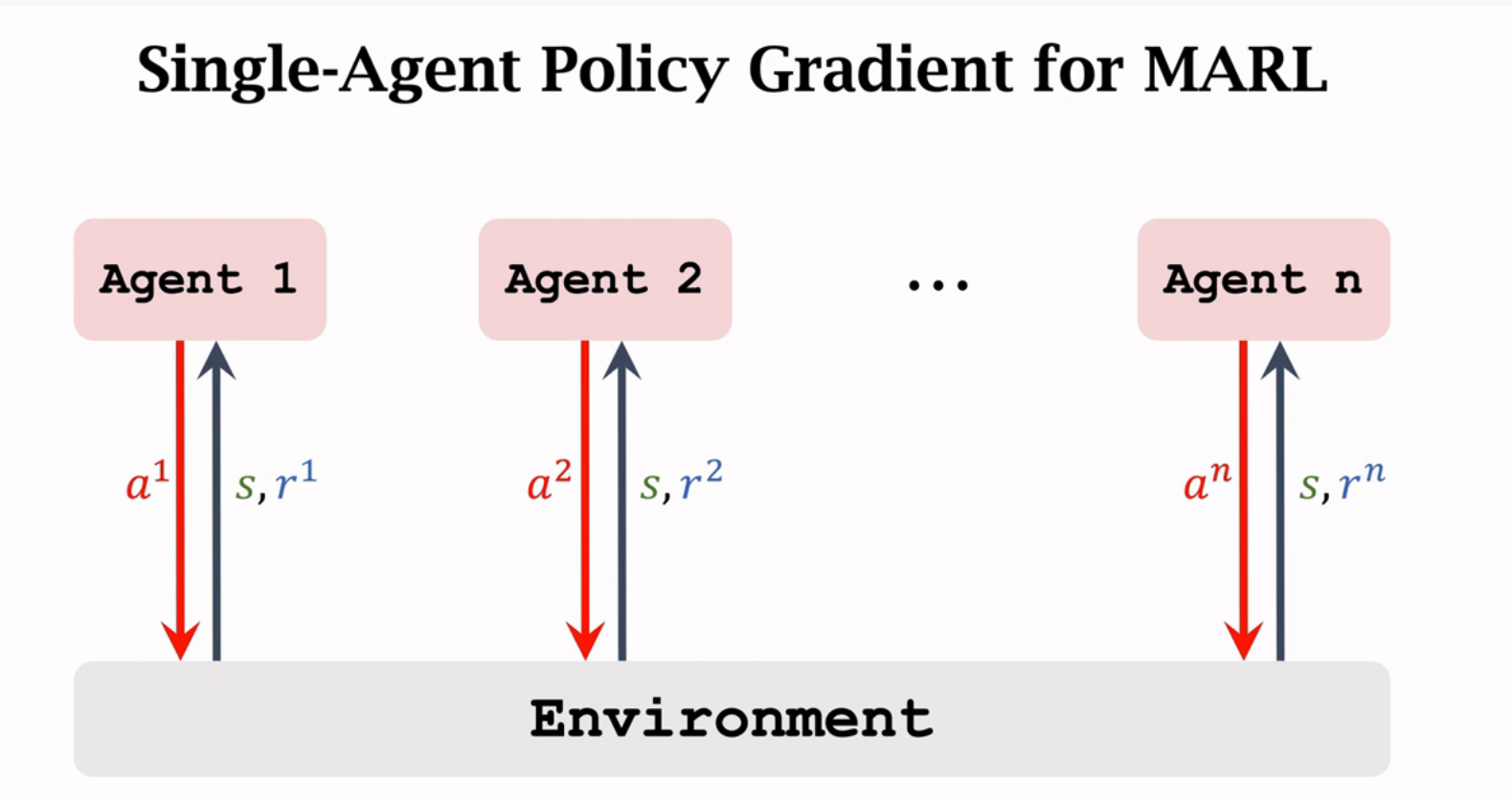



Summary



Multi-Agent RL的三种架构
multil-agent模型下,不同agent之间要通信来共享信息,通信方 式主要是中心化和去中心化




每个agent只能观察到部分,没有充分信息来做决策,所以让中央控制器来做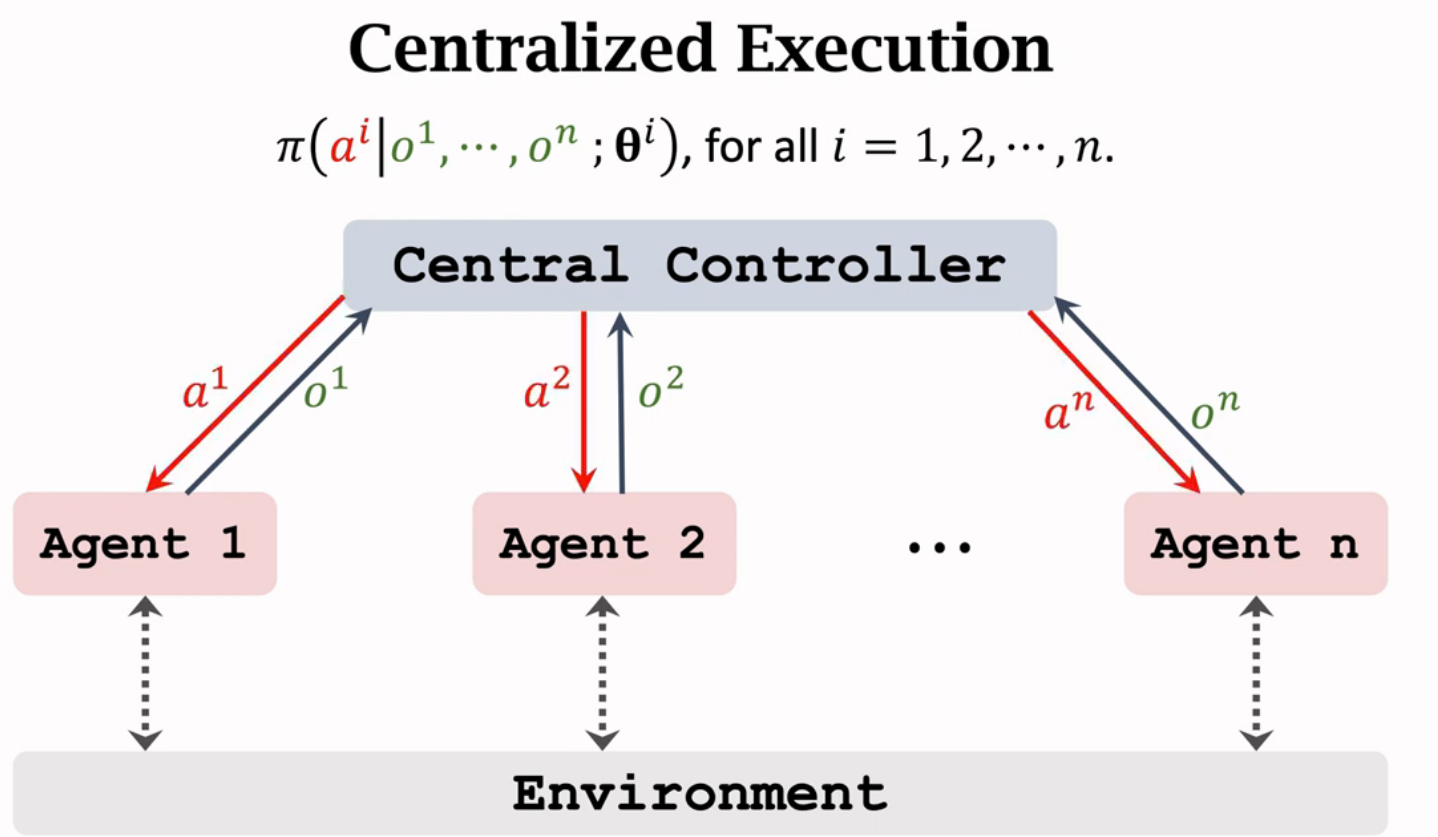











Summary



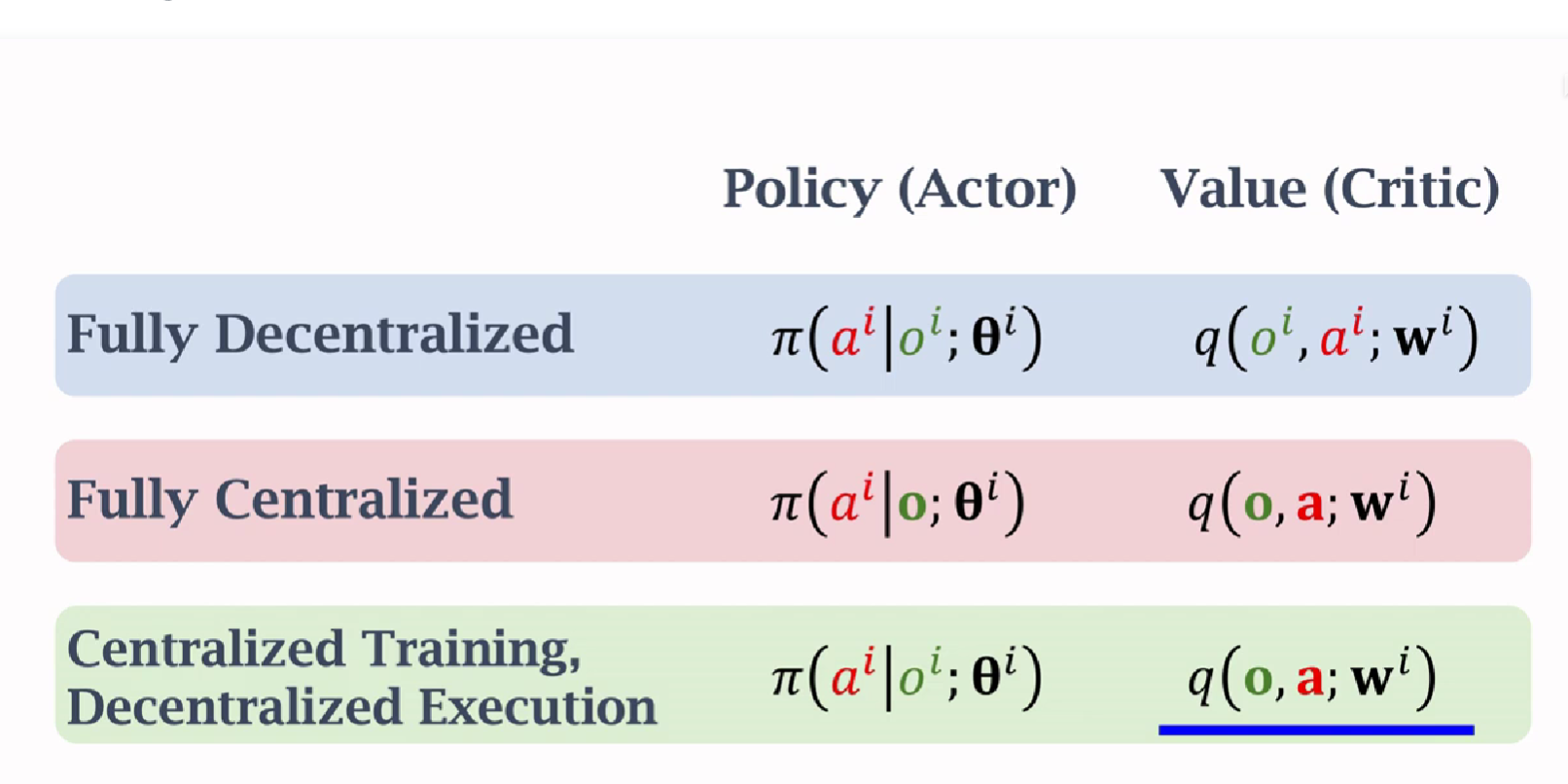
关于multi-agent,王老师推荐的综述论文


